钻柱黏滑振动特性仿真与产生机理分析

付蒙, 李江红, 吴亚锋, 李嫣然

(1.西北工业大学 动力与能源学院; 2.西北工业大学 航海学院, 陕西 西安　710072)



钻柱黏滑振动特性仿真与产生机理分析

付蒙1, 李江红1, 吴亚锋1, 李嫣然2

(1.西北工业大学 动力与能源学院; 2.西北工业大学 航海学院, 陕西 西安710072)

摘要：针对钻探作业中产生的钻柱黏滑振动现象,研究了仿真环境下钻柱系统的黏滑振动特性与振动产生机理。基于振动理论,建立了井下钻进系统的双自由度弹性模型,提出了一种模拟钻头-岩石摩擦力矩的算法;构造了钻进系统结构图,模拟了钻柱黏滑振动的变化规律,并通过极限环分析钻柱黏滑振动的产生机理;绘制钻井参数与振动幅值和周期的关系曲线,讨论了钻井参数对钻柱黏滑振动的影响。仿真结果表明,钻柱黏滑振动主要表现为钻头周期性地黏滞和滑动,属于一种由非线性摩擦力引起的自激振动;钻井参数的改变影响钻柱黏滑振动的剧烈程度。

关键词：钻柱;黏滑振动;弹性模型;特性仿真;产生机理

石油与天然气的勘探作业中,钻井设备受到摩擦、压强、岩石质地等不确定因素影响,容易引发钻柱黏滑振动现象。钻柱的剧烈振动是引起钻柱失效事故占钻井事故的主要原因[1]。剧烈的黏滑振动发生时,井底钻具组合(BHA)的瞬时速度会增加到正常转速的3～9倍,非常容易破坏钻井设备[2]。因此研究钻柱黏滑振动的动力学特性,分析振动产生机理具有现实的经济效益。

近年来,随着随钻测井技术的发展,钻柱动力学的研究取得了很大的进展。Richard 和Detournay基于振动扭摆原理,用弹簧来模拟钻柱,用刚性飞轮来模拟BHA,建立了钻柱黏滑模型[3-4]。Khulief通过拉普拉斯变换求解钻柱动力模型的方程式,解释了扭转向弯曲惯性组合引发钻柱黏滑振动的原因[5]。文献[6]在对岩石摩擦扭矩进行简化的基础上,给出了钻柱产生黏滑振动的判别式,分析了钻柱黏滑振动的影响因素。国内在钻柱黏滑振动分析及控制方面相对比较落后,还存在比较多的问题:仅仅针对钻进系统进行数值仿真,尚缺少对钻柱系统的结构仿真,制约了控制算法的研究;现有的摩擦模型无法准确描述钻头零速区域摩擦扭矩的连续性,而且没有提出有效的方法将摩擦模型与钻进系统动力模型结合;缺少针对钻井参数影响钻柱黏滑振动的研究;抑制钻柱黏滑振动算法落后,距离工程应用的差距很大。

文章以井下钻进系统为研究对象,将钻柱-井底钻具组合简化为双自由度动力模型,分析系统的运动方程式;建立了Karnopp摩擦模型[7],有针对性地提出一种新算法,解决黏滑状态分界点处的连续性问题;基于MATLAB实现系统的结构仿真,模拟了钻井过程中黏滑振动的产生过程和运动规律,首次实现了对钻头摩擦扭矩磁滞效应的仿真;绘制钻井参数影响黏滑振动的变化曲线,为优化钻井参数以及研究抑制钻柱黏滑振动的方法奠定理论基础。

1钻柱黏滑振动模型建立

1.1井下钻进系统动力模型

实际钻井中,通过改变井架大钩载荷和井口钻压来调节竖直方向的受力,因此在构建井下钻进系统的模型时可以忽略竖直方向的受力。如图1所示,基于双自由度扭力振动原理,用弹簧-转动惯量模型简化井下钻进系统[8],并做如下假设:

1) 井下钻进系统简化为钻柱和2个刚性飞轮;

2) 整个钻进系统的转动惯量集中于刚性飞轮;

3) 忽略BHA的扭曲特性,钻柱简化为具有一定刚度的弹簧。

图1　井下钻进系统双自由度模型

图1a)中m为电机的驱动扭矩,mf为钻头受到的摩擦扭矩。图1b)中J1为第一自由度转动惯量,φ1为钻柱顶端角位移,ω1为钻柱的驱动转速,C1为第一自由度阻尼系数(钻柱顶端阻尼系数);J2为第二自由度的转动惯量,φ2为BHA的角位移,ω2为BHA的角速度,C2为第二自由度的阻尼系数;K为弹簧的弹性系数(钻柱的扭转刚度系数)。根据钻柱静力学可知,系统的弹性系数K

(1)

式中,D为钻杆外径,d为钻杆内径,L为钻柱长度,G为钢剪切模量G=7.96×1010N/m2。

系统的阻尼系数C

(2)

式中,cdp为单位长度钻杆阻尼系数,Li表示第i自由度钻柱长度。

系统的有效转动惯量J

(3)

式中,Jco为钻铤转动惯量,Jbit为钻头转动惯量。

1.2钻头所受岩石的摩擦扭矩模型

钻头与岩石之间的作用力与岩石的性质和钻头的运动状况有关,破坏岩石时作用于剪切面上的应力大于作用于剪切面上的摩擦阻力。钻头的摩擦力是连续非线性的,其摩擦扭矩可以表示为以钻头转速为自变量的函数。为准确描述钻头零速区域摩擦扭矩的连续性,利用Karnopp摩擦模型模拟钻具受到的摩擦扭矩[8],如图2所示。

图2　摩擦扭矩模型

图2中M0为库仑摩擦扭矩,Ma为最大静摩擦扭矩,[-Δω,Δω]被称为“速度死区”,当ω2∈[-Δω,Δω]时认定钻具进入黏滞状态,摩擦力与作用在系统上的其他力平衡。直到驱动力超过最大静摩擦力时,进入滑动状态。Karnopp摩擦模型是介于动态摩擦和静态摩擦的一种简化模型,可以规定其静态区间。用mdp表示钻柱传递给BHA的驱动转矩,Karnopp摩擦模型表达式

(4)

1.3系统状态分析与结构图

通过对双自由度模型的受力分析,第一自由度微分动力方程

(5)

第二自由度微分动力方程

(6)

其拉普拉斯变换

(7)

对于第二自由度有

其拉普拉斯变换

(8)

文献[1]提出了利用解析微分方程的方法仿真钻柱黏滑振动,但是现有研究缺少针对钻柱系统结构的仿真。文章将2个自由度结构联立,创新性地构建如图3所示的井下钻进系统结构图。结构图以电机的驱动扭矩m为输入,以钻头角速度ω2为输出。图3中mf(ω2)子模型为构造的Karnopp摩擦模型,满足非线性动态系统的要求,实现了对非线性摩擦力矩的模拟。

图3　井下钻进系统双自由度结构图

2钻柱黏滑振动的运动规律

通过对井下钻进系统的受力分析,构建非线性动态系统的结构图,在MATLAB中实现了对钻柱黏滑振动的仿真。通过黏滑仿真获得系统的动态响应曲线,模拟钻柱黏滑振动的产生过程和钻头的运动规律。以陕北榆林地区中石油一号井一次钻采过程为例,钻井设备规格:钻杆外径D=127 mm、内径d=108 mm、长度l=5 m,钻铤外径Dco=209 mm、内径dco=108 mm、长度lco=150 m,钻头转动惯量Jbit=164 kg·m2,单位钻杆阻尼系数cdp=0.032 Ns/rad。井队安装顶驱系统,驱动电机由变频器控制,当钻井深度达到2 000 m时,其输出转矩为3 200 Nm、驱动转速为60 r/min。大钩载荷与井口压力的合力大约等于70根钻杆重力，为了便于仿真分析,对钻进系统结构做进一步简化。根据钻井部件参数,求得黏滑模型的弹性系数、阻尼系数和转动惯量,如表1所示。

表1　模型参数

为提出有效的方法将摩擦子模型与钻柱黏滑模型结合,在仿真中,利用Karnopp摩擦模型模拟钻头摩擦扭矩,并作为系统模型反馈环节的一部分。如图4所示。

图4　钻头摩擦力矩算法

设计了一种算法应用于仿真模型,填补了实现钻柱系统结构仿真的空白。

图5为时域900～1 000 s,稳定状态下钻头角速度、BHA驱动扭矩、摩擦扭矩和钻头角位移-角速度相轨迹的仿真结果。从图5a)、图5d)中可以看到明显的钻柱黏滑振动现象,其主要表现为在一段时间内钻头静止不动,钻柱积累能量,当钻柱扭矩超过摩擦扭矩时钻头突然高速旋转,并在钻柱能量循环条件下钻头的滑动与黏滞周期性地交替。图5b)通过BHA扭矩的变化规律反应钻头角速度的变化率,图5c)反应摩擦扭矩的变化规律,且钻柱驱动扭矩等于BHA驱动扭矩与摩擦扭矩之和。

图5中,黏滑振动的周期T≈5 s,角速度振幅ω2≈140 r/min,仿真结果与文献[8]中的钻采监测结果(图3.1)吻合较好;ω1=60 r/min时,ω2≈140 r/min,表明滑动阶段的速度峰值超过电机驱动转速的2倍;一个黏滑周期内系统的输入能量与系统的消耗能量达到平衡,其中使能量平衡的振幅值即为黏滑振动达到稳定时的最大转速。

图5　钻柱黏滑振动的运动规律

从图5d)可知,在低速区域0～20 r/min范围内,钻头角速度下降速率比上升速率低。为研究该特征,绘制单个周期内摩擦扭矩与钻头角速度的关系曲线,如图6所示。图6表明速度减小时的摩擦力要比速度增加时摩擦力大,摩擦力矩表现出明显的磁滞效应。

图6　摩擦扭矩磁滞效应

与稳定状态图5d)不同,图7描述了0～600 s钻柱黏滑振动从初始态到稳定态的变化过程。

图7　钻柱黏滑诱发阶段极限环

如图7所示,在钻柱产生黏滑的初级阶段,系统蕴含的动能和弹性势能比较小,系统总能量周期性增加。对整个钻进系统而言,驱动电机为系统提供恒定能量。当钻进系统受到激励后,系统自身运动状态以及能量反馈受到非线性摩擦力调节,使系统耗散的总能量趋近于输入的总能量,系统维持等幅振动。因此,钻柱的黏滑振动具有非线性自激振动的特征,是由非线性摩擦力引起的自激振动。

3钻井参数对黏滑振动的影响

上述结果基于钻井部件结构参数不变的条件获得,然而随着钻进的深入,钻井参数不断改变,钻柱黏滑振动的剧烈程度随之改变。文章分别改变钻柱长度、驱动转速和井口钻压,展开相应的仿真研究。讨论了钻井参数对钻柱黏滑振动的影响,总结出一些减振的措施,使钻柱的有效扭矩达到最大。

1) 钻柱长度改变对钻柱黏滑振动的影响，如图8所示。

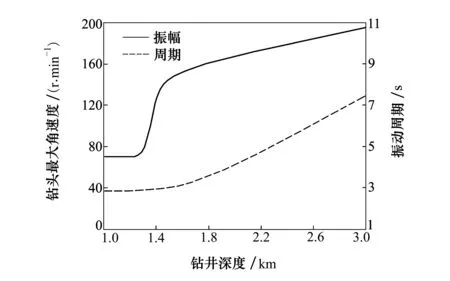
图8　黏滑振动与钻柱长度的关系拟合曲线

当L<1 300 m时黏滑振动不会发生,此时对应的钻柱长度被称为临界长度;当L>1 400 m时发生黏滑振动,且随着钻柱长度的增加,振动幅值增加,振动周期变大;当1 300 m≤L≤1 400 m时黏滑振动具有不确定性。仿真结果表明,黏滑振动表现为低频振动,且在深部地层钻进时更加容易产生黏滑振动,钻井深度增加导致黏滑振动更加剧烈。

2) 钻柱长度改变对钻柱黏滑振动的影响。如图9所示,驱动转速ω1越低,振动的周期越大,黏滞时间越长;随着ω1的增加,ω2的幅度增大,但是变化率减小;并且ω2>2ω1恒成立,与仿真图5结论符合。因此,可以通过升高驱动转速的措施来减小钻柱黏滑振动强度,但是该方法很难使振动消除。

图9　黏滑振动与井口驱动转速的关系拟合曲线

3) 井口钻压的大小对钻柱黏滑振动的影响。图10为黏滑振动的振幅和周期与井口钻压p的关系拟合曲线,阐释了钻柱黏滑振动诱发、产生、卡钻的全过程。当p<85kN时，为正常钻进状态,受到钻柱刚度和动摩擦力影响,ω2有轻微波动,不存在黏滑振动；当85kN≤p≤105kN时，mf增大,系统进入黏滑状态；当钻压继续增大时,系统会进入混沌状态；该状态下钻柱聚积大量能量后克服静摩擦力,大量势能瞬间释放,ω2可以达到ω1的几倍以上,对BHA损伤特别大。当p>110kN时，钻头卡钻，如果不调整钻井参数,钻柱可能会被扭断。综上所述,随着钻压的增大,钻头黏滞时间更长,振动频率更低;适当减小井口钻压,可以有效地避免钻柱黏滑振动的产生。

图10　黏滑振动与井口钻压的关系拟合曲线

4结论

文章中构建的钻柱系统结构,准确地实现了对钻柱黏滑振动变化规律的特性仿真,完成了对钻柱黏滑振动产生机理的分析,并讨论了钻井参数对钻柱黏滑振动的影响,为求解抑制黏滑振动的算法奠定了理论基础。研究结果表明,钻柱黏滑振动是由钻头受到的非线性摩擦力引发的自激振动,主要表现为钻头的黏滞和滑动交替出现;钻井深度增加、驱动转速过低、钻压过大均会加剧钻柱黏滑振动的强度。有关抑制钻柱黏滑振动算法的实现还需要进一步的工作。

参考文献：

[1]韩春杰, 阎铁. 深井钻柱振动规律的分析及应用[J]. 天然气工业, 2005, 25(9): 76-79

Han Chunjie, Yan Tie. Analysis on Drill String Vibration of Deep Wells[J]. Natural Gas Industry, 2005, 25(9): 76-79 (in Chinese)

[2]Nicholas V, Chien-Min L, Balakumar B, et al. Stick-Slip and Whirl Motions of Drill Strings: Numerical and Experimental studies[C]∥ASME Design Engineering Technical Conference, 2011: 829-838

[3]Richard T, Detournay E. Self-Excited Stick-Slip Vibrations of Drill Bits[J]. Comptes Rendus Mecanique, 2004, 332(8): 619-626

[4]Depouhona A, Detournay E. Instability Regimes and Self-Excited Vibrations in Deep Drilling Systems[J]. Journal of Sound and Vibration, 2014, 333(7): 2019-2039

[5]Khulief Y A, Al-Sulaiman F A, Bashmal S. Vibration Analysis of Drill Strings with String Borehole Interaction[J]. Journal of Mechanical Engineering Science, 2008, 222(11): 2099-2110

[6]Huang Genlu, Han Zhiyong. Mechanism Analysis on Torsional Stick-Slip Vibration of Drillstring in Extended Reach Well and Some Ways to Its Suppression[J]. Petroleum Drilling Techniques, 2001, 29(2): 4-6

[7]Karnopp D. Computer Simulation of Slip-Stick Friction in Mechanical Dynamic[J]. Journal of Dynamic Systems, Measurement, and Control, 1985, 107: 100-103

[8]Jansen J D. Nonlinear Dynamics of Oil Well Drill-Strings[D]. Delft, Delft University, 1993

收稿日期：2015-10-27

作者简介：付蒙(1987—)，西北工业博士研究生，主要从事测试、热工程信息处理、状态监测与故障诊断及钻柱动力学研究。

中图分类号：TE92

文献标志码：A

文章编号:1000-2758(2016)03-0467-06

Characteristic Simulation and Mechanisms Analysis for Drill-Strings Stick-Slip Vibration

Fu Meng1, Li Jianghong1, Wu Yafeng1, Li Yanran2

1.School of Power and Energy, Northwestern Polytechnical University, Xi′an 710072, China 2.School of Marine Engineering, Northwestern Polytechnical University, Xi′an 710072, China

Abstract:To our best knowledge, there is no paper in the open literature concerning the structural simulation for drill-strings stick-slip vibration. In order to improve both the productivity and the quality of the drilling and, thus, attenuate the intensity of vibration, we commit to analysis the dynamic characteristics and produce mechanism of the drill-strings stick-slip vibration. In the full paper, we explain in detail our simulation research results; in this abstract, we just add some pertinent remarks to the three topics of explanation: (1) dynamic model of the drill-strings drive; (2) the special law of motion of drill-strings stick-slip vibration; (3) the effect of drilling parameters; the subtopics of topic 1 are the double degrees of freedom model (subtopic 1.1), the Karnopp drill-tool friction sub-model (subtopic 1.2), and the structure diagram of the system as shown in Fig.3 in the full paper (subtopic 1.3); under subtopic 1.2, Fig.2 in the full paper avoids the problem of non-unique friction description in the zero-speed region of drilling-tool; under subtopic 1.3, we derive eqs. (7) and (8); under topic 2, we propose a new algorithm to apply the Karnopp friction sub-model to the simulation as shown in Fig.4 in the full paper, the phenomenon of drill-strings stick-slip vibration is simulated by MATLAB as shown in Fig.5 in the full paper, we point out that drill-strings stick-slip vibration exist hysteresis effect as shown in Fig.6 in the full paper, and we analyze the limit cycle of nonlinear drill-strings system which reflect the energy change of the system and the producing mechanism of vibration as shown in Fig.7 in the full paper; under topic 3, Fig.8, Fig.9 and Fig.10 in the full paper show the amplitude and frequency of stick--slip oscillation change curve which abscissa respectively corresponded to drill string-length, driving speed and weight-on-bit (WoB). The simulation results indicate preliminarily that: (1) the undesired drill-strings stick-slip vibration belongs to a self-excited vibration and is caused by the nonlinear friction which gives rise to the imbalance between the kinetic energy and potential energy of both ends of the drill-strings; (2) adjusting drilling parameters can effectively suppress the stick-slip vibration of the drill-strings.

Keywords:characteristic simulation, mechanisms analysis, drill-strings stick-slip vibration, structural analysis, dynamic model, law of motion, double degrees of freedom, Karnopp friction model, equations of state, differential equation, Laplace transform, algorithm, MATLAB, hysteresis effect, limit cycle, nonlinear drill-strings system, weight-on-bit (WoB), self-excited vibration