针对相关性衰减的子阵子空间降秩检测及最优子阵划分

邵炫, 孙超

(西北工业大学 航海学院, 陕西 西安　710072)



针对相关性衰减的子阵子空间降秩检测及最优子阵划分

邵炫, 孙超

(西北工业大学 航海学院, 陕西 西安710072)

摘要：针对海洋波导环境下空间相关性衰减导致检测性能下降的问题进行研究。结合子空间降秩和子阵处理，提出了子阵子空间降秩检测方法并对其检测性能进行分析。结果表明，在相关性衰减的情况下，该检测方法能够获得比全阵列处理更好的检测性能。同时研究了子阵划分对子阵检测性能的影响，并给出了空间相关性衰减下的最优子阵划分方法。研究发现：最优子阵长度和信号相关长度之间存在一定的比例关系；当子阵长度与相关长度比值的取值范围为1～2.5时，可以获得最佳的检测效果。最后针对特定海洋波导环境，利用蒙特卡罗方法进行仿真验证。

关键词：空间相关性；指数幂律相关性模型；卡方分布；子阵目标检测；最优子阵划分；水下声学；特征值；特征向量；最大似然；蒙特卡罗方法；信号处理；信噪比

随着目标减震降噪技术的发展，声呐设备逐渐呈现低频化，大孔径基阵得到广泛的应用，相应的阵列处理方法和性能受到关注。现有的大多数阵列处理模型都假设基阵接收的声源辐射信号完全相关，由此获得了理想的处理效果。然而在实际海洋环境中，随着基阵尺度不断增大，不同阵元接收信号之间会出现空间相关性衰减的现象[1-4]，其衰减程度常用空间相关系数来描述。当不同阵元的空间相关系数下降到一定值(通常为1/e)时，可认为接收信号彼此不相关，从而导致基于理想假设模型的阵列处理性能下降[5-8]。此时两阵元之间的距离被定义为空间相关长度。建立非完全相关信号的阵列处理模型及相应的处理方法与实际更加吻合，也十分必要。本文将主要针对如何提高相关性衰减情况下大孔径拖曳阵检测性能的问题进行研究。

子阵处理[9-12]是根据实际需求，利用不同的子阵划分方法[13-14]把阵列划分成若干小的子阵列并对子阵输出进行联合处理的信号处理方法。它常用于改善分布声源条件下目标检测和方位估计的性能，但利用子阵处理方法来改善相关性衰减下的检测性能却鲜有提及。由于信号空间相关性衰减与空间间隔成正比，选取合适的子阵长度可以减小相关性衰减对阵列处理性能的影响。根据文献[12]，对于子阵匹配场波束形成，当子阵长度大约为空间相关长度的2倍时，其信噪比增益与最优信噪比增益的差值最小，仅为1 dB。因此，我们认为采用子阵处理对大孔径拖曳阵在相关性衰减条件下的检测性能有改善作用。

子空间降秩是一种常用的降维方法[15-19]，它通过特征分解(奇异值分解)或联合迭代优化等方法构造一个降维子空间，并把数据投影到该子空间中达到降维的目的。该方法舍弃了无关的噪声成分并很大程度地保留了主要的信号成分，因此对模型失配和噪声干扰有较高的稳定性同时减小了计算的复杂度。文献[15,18]中，利用子空间降秩方法有效地改善了由于角扩展引起的检测性能下降问题。

本文针对海洋波导环境中空间相关性衰减的现象，结合子空间降秩和子阵处理，提出了子阵子空间降秩检测方法并对其性能进行研究。同时，着重分析了子阵划分对子阵检测性能的影响，给出了空间相关性衰减下的最优子阵划分方法。文章最后针对特定波导环境，利用蒙特卡罗方法对子阵检测方法的性能进行仿真验证。

1问题描述

1.1阵列信号模型

假设接收阵为一个M元水平均匀线列阵,基阵接收信号x可以表示为

(1)

1.2空间相关矩阵

(2)

式中,Es为信号功率,Rs为归一化的信号空间相关矩阵,E{·}表示数学期望,C为信号相关系数矩阵,G为表征信道传递函数的矩阵。

信号相关系数矩阵C的元素cij为均匀水平线列阵第i个阵元和第j个阵元接收信号之间的相关系数。在阵列信号处理研究中通常假设基阵中各个阵元接收信号完全相关,此时矩阵C为全1矩阵。但在实际海洋环境中,受信道特性等多种因素的影响,不同阵元接收信号之间的相关性随距离的增大而下降,导致矩阵C中远离主对角线的元素逐渐减小。信号空间相关性通常用相关长度(定义为相关系数下降到一定值时对应的2个阵元之间的距离,本文取1/e)来表述。本文采用一种常见的描述海洋环境中信号空间相关系数的模型——指数幂律模型对空间相关矩阵进行建模[7-8,12]。在该模型中,均匀水平线列阵第i个阵元和第j个阵元接收信号之间的相关系数cij可以表示为

(3)

式中,L为相关长度,a为阵元间距,模型参数q控制信号相关性衰减的快慢程度,值越大衰减越快。一般来说,q≤2是比较常见的取值范围,文中假设q=1。

(2)式中的矩阵G是一个由各接收阵元对应的声信道频率响应组成的对角阵,其表达式为

(4)

式中,gm为第m个阵元对应的声信道频率响应函数。为了简化计算使得各个阵元接收信号的功率相同,对各阵元对应的声信道频率响应函数进行归一化,得

(5)

1.3二元假设检验

二元假设检验是水下目标检测中常用的检测手段,它定义只存在噪声的情况为零假设H0,信号和噪声同时存在的情况为备选假设H1。当检验统计量大于给定的门限时,判定备选假设H1成立,否则判定零假设成立。

对于全阵列接收数据x,其二元假设可以表示为

(6)

根据文献[20-21],假设H0和H1下的概率密度函数分别为

(7)

(8)

式中,矩阵Rn=E{xxH}=σ2IM和Rsn=E{xxH}=EsRs+Rn分别为随机变量x在零假设和备选假设下的空间相关矩阵,矩阵Qn和Qsn分别为零假设和备选假设下的采样协方差矩阵,函数tr(·)表示矩阵的迹。根据(7)式和(8)式推导出x的对数似然比函数,略去常数项得到相应的检验统计量的表达式为

(9)

式中,w为对应的似然比检测权值。

若检验统计量L(x)大于给定的门限γ,则判定备选假设H1成立,即同时存在信号和噪声;反之,则判定备选假设H0成立,认为只有噪声存在。

2子阵子空间降秩检测

2.1检测算法

子阵子空间降秩检测是把整个接收阵列分成若干小的子阵列,对各子阵接收数据应用子空间降秩波束形成[22],并对各子阵输出进行联合处理的检测方法。各子阵输出间的联合处理分为相干处理和非相干处理2种方式。相干处理是对各子阵输出信号进行相干叠加处理,而非相干处理则是对各子阵输出能量进行叠加处理。本文仅考虑非相干处理的情况。

将整个阵列划分为非重叠的P个等长度子阵,每个子阵的阵元个数为M/P。根据(9)式,第p个子阵对应的似然比检测权值wp可以表示为

(10)

式中,矩阵Rsp为矩阵Rs中与第p个子阵对应的块矩阵,Rnp是矩阵Rn中与第p个子阵对应的块矩阵。

(11)

式中,矩阵Urp=[u1p,u2p,…urp]的列向量为矩阵Rsp前r个较大特征值(特征值按降序排列λ1p≥λ2p≥…≥λrp≥0)对应的特征向量;矩阵Σrp为一对角阵,可以表示为

(12)

式中,λip,i=1,2,…,r为矩阵Rsp前r个较大特征值中的第i个特征值。

非相干子阵子空间降秩的加权矩阵weig-s可以表示为由各子阵加权向量wp-eig,p=1,2,…,P组成的块对角阵[10]

(13)

由(10)式结合加权向量可以得到

(14)

在本文后续处理中,以(14)式作为非相干子阵子空间降秩检测的检验统计量。

2.2理论检测性能推导

文献[13]对全阵列子空间降秩检测的性能进行了详细分析,本文在此基础上利用其采用的近似方法对非相干子阵子空间降秩检测的理论性能进行推导。

由于输入信号x为服从正态分布的零均值复高斯随机变量,其空间相关矩阵与假设条件(零假设或备选假设)有关,因此检验统计量为假设条件的函数。又因为输入信号x是服从正态分布的零均值复高斯随机变量,式(14)中的检验统计量可以改写为

(15)

(16)

式中,λp,1≥λp,2≥…≥λp,r≥0为矩阵Rsp前r个较大特征值。

根据(15)式,非相干子阵子空间降秩检测的检验统计量可以看作K×P×r个随机变量的加权和,这些随机变量都服从自由度为2的中心化卡方分布。实际应用中,直接计算其检测概率存在很大的困难[23],因此这里对检验统计量d(x,Hl)的分布采用近似处理,将其近似看作是服从自由度为Nl的加权卡方分布的随机变量[13],即

(17)

式中,非零加权κl和自由度Nl分别满足

(18)

根据卡方分布的理论检测概率,并结合(17)式,可以得到非相干子阵降秩检测的理论检测概率为

(19)

由(19)式可以看出,非相干子阵子空间降秩检测的理论检测概率由非零加权和自由度决定,它们都是子阵个数的复杂函数。

2.3相关性衰减下的最优子阵划分

本节主要研究信号空间相关长度对子阵划分后阵列处理增益和检测性能的影响,并由此给出一种最优子阵划分方式,因此假设各子阵相互之间没有重叠且阵元个数相同,此时各子阵空间相关矩阵具有相同的特征值。

由(18)式可知,当r=1时非零加权κl和自由度Nl可以改写为

(20)

(21)

式中,Γ(·)为伽马函数,γ(·)为不完全伽马函数。根据(20)式和(21)式,检测概率PD可以改写为

(22)

由(20)式和(22)式可知,自由度Nl与参数b是子阵长度Ls的单调减函数,而矩阵Rsp的最大特征值λp,1是子阵长度Ls的单调增函数函数,则对于固定的相关长度,子阵长度Ls增大会同时引起自由度Nl和能量因子σd的减小。但是根据(22)式,检测概率PD分别是自由度Nl(Nl为大于等于2的整数)的单调增函数和能量因子σd的单调减函数。因此当子阵长度Ls增大时,检测概率PD的大小取决于自由度Nl和能量因子σd的变化程度,且总会存在一个或几个子阵长度Ls使得检测概率PD达到最大。另一方面,因为特征值λp,1的大小与相关长度有关,所以对于不同的相关长度L,使检测概率PD达到最大的子阵长度Ls不同。

据此,本文提出一种相关性衰减下的最优子阵划分方法,对于大孔径线列阵,可以使检测器的检测性能达到最优。该方法首先利用理论检测概率公式((22)式),计算出不同子阵划分情况对应的理论检测概率,然后选出理论检测概率最大值对应的子阵个数作为最优子阵个数,最后根据子阵长度与子阵个数的关系计算出最优子阵长度。

由文中假设条件可知,各子阵阵元个数相同且相互之间没有重叠。对于非连续孔径的线列阵,不同子阵个数对应的子阵长度Ls是有限且离散的。因此,将子阵长度Ls可能取到的值一一代入(22)式进行计算,最大检测概率对应的子阵长度即为最优子阵长度Ls-opt。

3仿真结果及分析

仿真分为理论性能仿真和蒙特卡罗仿真两部分,分别检验了非相干子阵子空间降秩检测方法的理论和实际检测性能。

3.1理论性能仿真

本节主要对上文给出的理论分析进行仿真,并通过计算结果对子阵子空间检测方法的检测性能及相关性衰减下的最优子阵划分进行说明。理论性能仿真中,接收阵为一均匀线列阵,阵长为500m,共有200个阵元,阵元间距为2.5m。声源辐射信号的中心频率为300Hz。

将阵列划分为等长度125m的4个子阵,图1给出了信号相关性存在衰减的情况下,全阵列检测和子阵子空间降秩检测方法的检测概率随输入信噪比的变化曲线和接收机工作特性(receiveroperatingcharacteristic,ROC)曲线,其结果由(19)式计算得到。其中信号相关长度为62.5m,图1a)中假设虚警概率为0.1,图1b)中固定输入信噪比为-19dB。由图1可知,对于不同的信噪比和虚警概率,子阵子空间降秩检测方法的检测概率总是高于全阵列处理;对于固定的虚警概率,随着信噪比的增加,子阵子空间降秩检测方法的优势越明显。

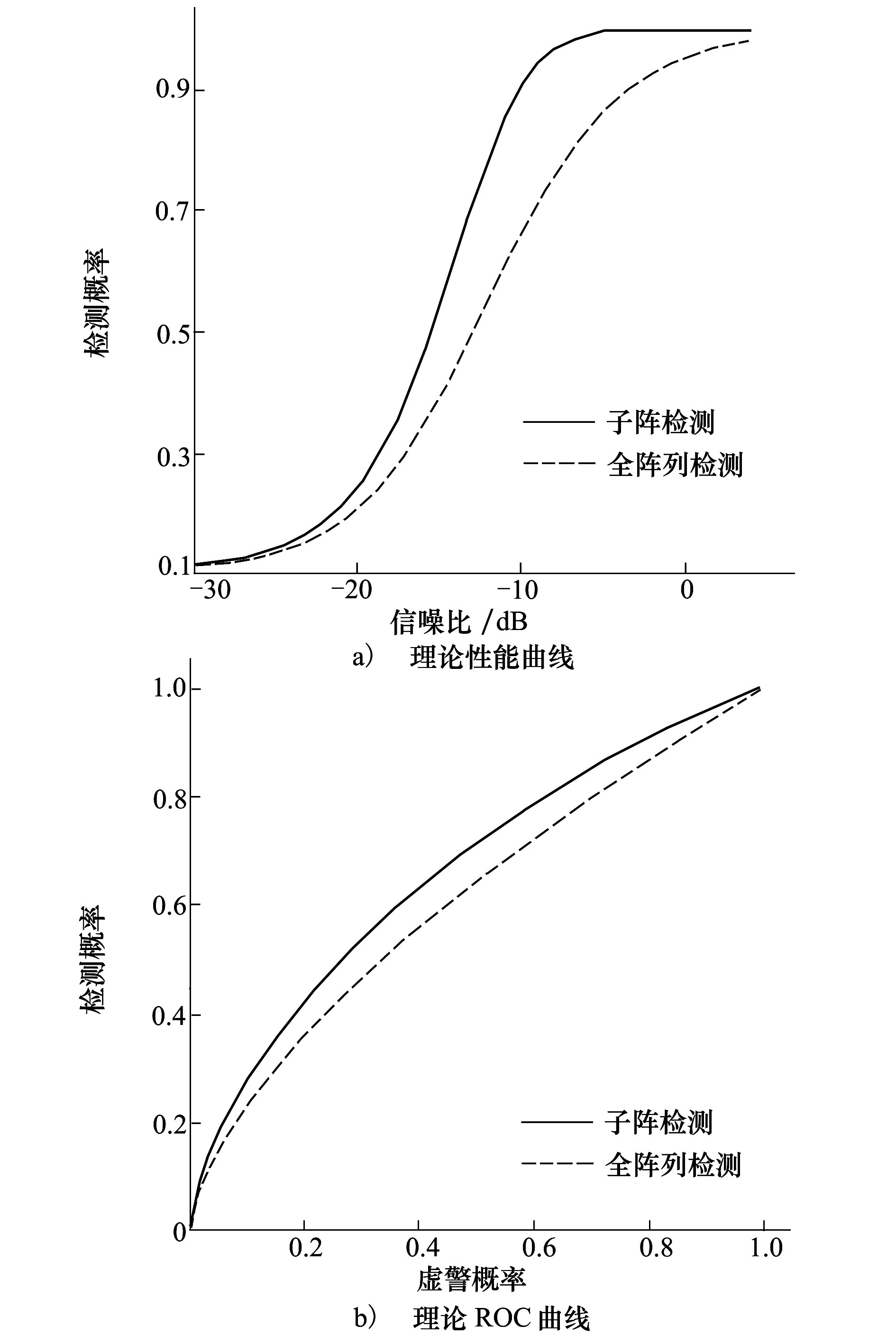
图1　　　　全阵列检测与子阵检测的理论检测性能　　　曲线和理论ROC曲线

图2描述了不同相关长度下与第p个子阵对应的信号相关矩阵最大特征值λp,1的下降程度。图

中,纵坐标代表特征值的下降程度,它定义为特征值的变化量与不考虑相关性衰减时矩阵特征值的比值。图中3个子阵长度25 m、62.5 m、250 m对应的子阵个数分别为20、8、2。可以看出,信号相关性衰减会导致归一化相关矩阵Rsp最大特征值λp,1的减小,且对于固定的相关长度,子阵长度Ls越大λp,1的下降程度越明显。

图2　特征值下降程度随子阵长度的变化曲线

图3给出了相关长度为25m和75m时,不同子阵划分长度对应的理论检测概率及检测概率随信噪比下降程度。图中,检测概率下降程度定义为检测概率的变化量与不考虑相关性衰减时检测概率的比值。可以看出,信号相关性衰减会降低子阵检测性能,且子阵长度越大检测概率下降程度越明显,这与特征值下降规律相同。

图3　不同信号相关长度下,检测概率和检测概率下降程度随信噪比的变化曲线

由2.3节分析可知,当相关长度固定时存在最优子阵长度Ls-opt使得检测概率PD达到最大,且对于不同的相关长度L,最优子阵长度Ls-opt不同。图4给出了当信噪比为-15 dB时,不同相关长度下理论检性能概率随子阵长度的变化趋势。由图4可以看出,最大检测概率对应的最优子阵长度Ls-opt随着相关长度的减小而减小,其长度大约是相关长度的2倍。

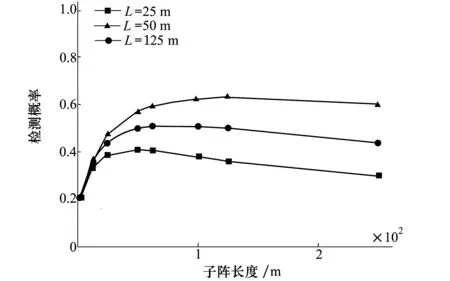
图4　检测概率随信号相关长度的变化曲线

为了进一步说明最优子阵长度与相关长度的关系,表1和表2给出了在不同采样快拍数和信噪比情况下,获得最大检测概率时最优子阵长度与相关长度的比值Ls-opt/L。根据表1,两者比值的取值范围大致在1～2.5之间,同时该比值随着信噪比的增大而减小。由表2可知,采样快拍数变化对比值Ls-opt/L影响不大。

由以上分析可知,信号相关性衰减会导致相关矩阵Rsp特征值的下降并降低子阵检测性能;不同子阵划分长度对应的下降程度不同,缩小子阵长度可以减小信号相关性衰减对检测性能的影响;对于固定信号相关长度,选取合适的子阵长度(最优子阵长度与相关长度比值Ls-opt/L的取值范围为1～2.5)可以获得最佳的检测效果;比值Ls-opt/L的大小是信噪比的减函数且受采样快拍数影响不大。

表1　不同信噪比情况下最大检测性能时子阵长度与相关长度的比值,K=5

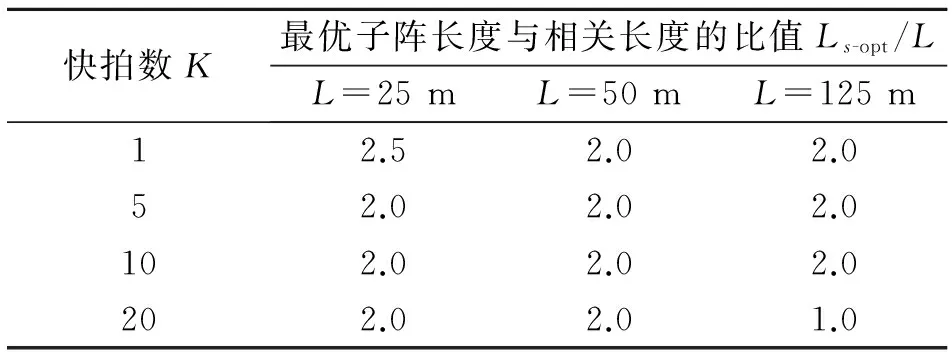
表2　不同快拍数情况下最大检测性能时子阵长度与相关长度的比值,信噪比为-19 dB

3.2蒙特卡罗仿真

本小节通过蒙特卡罗实验对空间相关性衰减情况下子阵子空间检测方法的检测性能和相关性衰减下的最优子阵划分方法进行仿真验证。

这里使用RAM程序[24]对浅海海域声场分布进行仿真计算。图5为环境参数及水平线列阵布放示意图。图中声源为一简谐声源,声源频率为300 Hz,深度为40 m,接收阵为一水平布放的均匀线列阵,布放深度100 m,阵元个数200个,阵元间距为2.5 m,接收阵元与声源最近距离为10 km,声源与阵列法线的夹角为36.9°。仿真海域水深为100 m,海水声速为1 500 m/s,海水密度为1 024 kg/m3,海底声速为1750 m/s,海底底质密度为1 900 kg/m3,吸收系数为0.3 dB/λ。

图5　声速剖面及水平线列阵布放仿真参数示意图

图6和图7分别给出了当K=1和K=5时,全阵列检测与子阵检测的检测性能曲线和ROC曲线。图中,标志为采用5 000次蒙特卡罗实验得到的仿真结果,曲线为检测方法的理论值,此时子阵长度为125 m,相关长度为50 m,检测性能曲线中虚警概率为0.1,ROC曲线中信噪比为-15 dB。可以看出,仿真结果和理论值十分接近且采样快拍数越大,接近程度越好;在相关性衰减的情况下,子阵子空间降秩检测方法能够获得比全阵列处理更好的检测性能。

为了验证最佳子阵长度与信号相关长度的比例关系,对子阵子空间降秩检测在不同相关长度、不同子阵长度下的检测概率进行了仿真,结果在表3和表4中给出。仿真过程中,采样快拍数K=5,虚警概率为0.1。根据表3当相关长度分别为25 m、50 m和125 m时,最佳子阵长度与相关长度的比值为2.5、1.25和1;而在表4中最佳子阵长度与相关长度的比值为2.0、1.25和1。表5给出了不同采样快拍数情况下,最优子阵长度与相关长度的比值,此时信噪比为-19 dB,虚警概率为0.1。根据表5,随着采样快拍数增加,比值有轻微的起伏,但没有超出1～2.5的范围。

可以看出其结果与上文理论分析的结果十分吻合,即对于固定的信号相关长度,当子阵长度与相关长度比值的在1～2.5范围内时,可以获得最佳的检测效果。

图6　当采样快拍数K=1时,子阵目标检测的检测性能曲线和ROC曲线　　　　　图7　当采样快拍数K=5时,子阵目标检测的检测性能曲线和ROC曲线

L/m检测概率PdLs=12.5mLs=25mLs=50mLs=62.5mLs=100mLs=125mLs=250mLs=500m250.3300.3670.4170.4180.3400.3520.2730.237500.3150.4130.4990.5210.5120.4860.4520.3531250.3110.4520.5560.5830.6710.7090.6730.604

表4　当信噪比为-15 dB时子阵降秩检测在不同相关长度、不同子阵长度的检测概率

表5　对于不同的相关长度和采样快拍数,最优子阵长度与相关长度的比值

4结论

本文针对海洋波导环境中空间相关性衰减的现象,结合子空间降秩和子阵处理,提出子阵子空间降秩检测方法并着重分析了子阵划分对检测性能的影响以及最优子阵长度和信号相关长度的关系。文中还针对特定海洋波导环境,利用蒙特卡罗方法对子阵检测方法的检测性能进行仿真验证。

理论分析和仿真结果表明,在相关性衰减的情况下,子阵子空间降秩检测方法能够获得比全阵列处理更好的检测性能;缩小子阵长度可以减小信号相关性衰减对检测性能的影响;对于固定的信号相关长度,当子阵长度与相关长度比值在1～2.5范围内时,可以获得最佳的检测效果;最优子阵长度与相关长度的比值Ls-opt/L是信噪比的减函数且受采样快拍数影响不大。

参考文献：

[1]DudaTF,CollisJM,LinYT,etal.HorizontalCoherenceofLow-FrequencyFixed-PathSoundinaContinentalShelfRegionwithInternal-WaveActivity[J].JAcoustSocAm, 2012, 131(2): 1782-1797

[2]刘宗伟, 孙超, 杜金燕. 不确定海洋声场中的检测性能损失环境敏感度度量[J]. 物理学报. 2013; 62(6): 64303

LiuZongwei,SunChao,DuJinyan.TheMeasureofEnvironmentalSensitivityinDetectionPerformanceDegradation[J].ActaPhysSin, 2013, 62(6): 643303 (inChinese)

[3]SpiesbergerJL.TemporalandSpatialCoherenceofSoundat250Hzand1 659kminthePacificOcean:DemonstratingInternalWavesandDeterministicEffectsExplainObservations[J].JAcoustSocAm, 2009, 126(1): 70-79

[4]DudaTF.TemporalandCross-RangeCoherenceofSoundTravelingThroughShallow-WaterNonlinearInternalWavePackets[J].JAcoustSocAm, 2006, 119(6): 3717-3725

[5]CareyWM.TheDeterminationofSignalCoherenceLengthBasedonSignalCoherenceandGainMeasurementsinDeepandShallowWater[J].JAcoustSocAm, 1998, 104(2): 831-837

[6]YangTC.MeasurementsofSpatialCoherence,BeamformingGainandDiversityGainforUnderwaterAcousticCommunications[C]∥ProceedingsofOCEANS2005, 2005: 268-272

[7]YangTC.AStudyofSpatialProcessingGaininUnderwaterAcousticCommunications[J].IEEEJournalofOceanicEngineering, 2007, 32(3): 689-709

[8]MontalbanoG,SerebryakovGV.OptimumBeamformingPerformanceDegradationinthePresenceofImperfectSpatialCoherenceofWavefronts[J].IEEETransonAntennasandPropagation, 2003, 51(5): 1030-1039

[9]WangWQ.Subarray-BasedFrequencyDiverseArrayRadarforTargetRange-AngleEstimation[J].IEEETransonAerospaceandElectronicSystems, 2014, 50(4): 3057-3067

[10]JinY,FriedlanderB.Reduced-RankAdaptiveDetectionofDistributedSourcesUsingSubarrays[J].IEEETransonSignalProcessing, 2005, 53(1): 13-25

[11]DoisyY,DeruazL,BeenR.InterferenceSuppressionofSubarrayAdaptiveBeamforminginPresenceofSensorDispersions[J].IEEETransonSignalProcessing, 2010, 58(8): 4195-4212

[12]MorganDR,SmithTM.CoherenceEffectsontheDetectionPerformanceofQuadraticArrayProcessors,withApplicationstoLarge-ArrayMatched-FieldBeamforming[J].JAcoustSocAm, 1990, 87(2): 737-747

[13]DhanatltwariAC,StergiopoulosS,PhillipsW,etal.AdaptiveBeamformingwithNear-InstantaneousConvergenceforMatchedFilterProcessing[C]∥IEEEConterenceonElectricalandComputerEngineeringCanadian, 1996: 683-686

[14]SwinglerDN.ALow-ComplexityMVDRBeamformerforUsewithShortObservationTimes[J].IEEETransonSignalProcessing, 1999, 47(4): 1154-1160

[15]JinY,FriedlanderB.DetectionofDistributedSourcesUsingSensorArrays[J].IEEETransonSignalProcessing, 2004, 52(6): 1537-1548

[16]ScharfLL,FriedlanderB.MatchedSubspaceDetectors[J].IEEETransonSignalProcessing, 1994, 42(8): 2146-2157

[17]WangX,AboutaniosE,AminM.Reduced-RankSTAPforSlow-MovingTargetDetectionbyAntenna-PulseSelection[J].SignalProcessingLettersofIEEE, 2015, 22(8): 1156-1160

[18]RaoAM,JonesDL.EfficientDetectionwithArraysinthePresenceofAngularSpreading[J].IEEETransonSignalProcessing, 2003, 51(2): 301-312

[19]DeLamareRC,Sampaio-NetoR.Reduced-RankSpace-TimeAdaptiveInterferenceSuppressionwithJointIterativeLeastSquaresAlgorithmsforSpread-SpectrumSystems[J].IEEETransonVehicularTechnology, 2010, 59(3): 1217-1228

[20]KaySM. 统计信号处理基础: 估计与检测理论[M]. 罗鹏飞,张文明,刘忠,赵艳丽,译. 北京：电子工业出版社, 2003: 837-838

[21]AndersonTW,AndersonTW,AndersonTW,etal.AnIntroductiontoMultivariateStatisticalAnalysis[M].ThirdEditionNewYork:Wiley, 1958: 69-70

[22] 杨志伟,贺顺,廖桂生,等. 子空间重构的一类自适应波束形成算法[J]. 电子与信息学报, 2012, 34(5): 1115-1119

YangZhiwei,HeShun,LiaoGuisheng,etal.AdaptiveBeam-FormingAlgorithmwithSubspaceReconstructing[J].JournalofElectronicsandInformationTechnology, 2012,34(5): 1115-1119 (inChinese)

[23]Castao-MartínezA,López-BlázquezF.DistributionofaSumofWeightedCentralChi-SquareVariables[J].CommunicationsinStatistics——TheoryandMethods, 2005, 34(3): 515-524

[24]CollinsMD.ASplit-StepPadéSolutionfortheParabolicEquationMethod[J].JAcoustSocAm, 1993, 93(4): 1736-1742

收稿日期：2015-10-27

基金项目：国家重点基础研究发展计划(6131870201)和国家自然科学基金(11274252、11534009)资助

作者简介：邵炫(1988—),西北工业大学博士研究生，主要从事水声信号处理研究。

中图分类号：TN911.7

文献标志码：A

文章编号:1000-2758(2016)03-0520-09

Reduced-RankSub-ArrayDetectionandtheOptimalSub-ArrayDivisionforSpatialCorrelationAttenuation

ShaoXuan,SunChao

(SchoolofMarineScienceandTechnology,NorthwesternPolythechnicalUniversity,Xi′an710072,China)

Abstract:In this paper, we consider the problem of detection performance degradation caused by the spatial correlation attenuation in the ocean environment. A reduced-rank detector is developed via combining the subspace Eigen Value Decomposition(EVD) with the sub-array processing，and the performance of the detector is evaluated. The results show that the reduced-rank detector using sub-arrays has a better performance than the full-array detector in the presence of imperfect correlation. Meanwhile, effects on the sub-array detection performance of the sub-array geometry are studied, and the optimal sub-array division method is proposed. We notice that there is a certain proportional relation between the optimal sub-array length and the signal correlation length, and that the optimal detection performance can be reached, as the ratio between the sub-array length and the correlation length is in the range of 1 to 2.5. The results are validated by computer simulations.

Keywords:spatial correlation; exponential-power-law modal; chi-square distribution; sub-array target detection; optimal sub-array division; underwater acoustics; eigenvalues; eigenvectors; maximum likelihood; Monte Carlo methods; signal processing; signal to noise ratio