基于CFD/CSD耦合的连结翼静气动弹性计算研究
张强, 祝小平, 周洲, 王伟
(1.西北工业大学 航空学院, 陕西 西安 710072; 2.西北工业大学 无人机特种技术重点实验室, 陕西 西安 710065)
基于CFD/CSD耦合的连结翼静气动弹性计算研究
张强1,2, 祝小平2, 周洲1,2, 王伟1,2
(1.西北工业大学 航空学院, 陕西 西安710072; 2.西北工业大学 无人机特种技术重点实验室, 陕西 西安710065)
摘要:针对某连结翼布局无人机,采用松耦合方式,耦合计算流体力学(CFD)和计算结构动力学(CSD)对其静气动弹性进行了计算研究;CFD求解模块采用非定常雷诺平均N-S方程,CSD模块采用直接积分法求解结构动力学方程,在时域内推进求解,收敛后获得静气弹计算结果。研究表明:连结翼静气弹变形后,前翼发生负扭转,后翼发生正扭转,前翼升力损失,后翼升力增加;无论是刚体构型还是静气弹变形后,前翼和后翼的展向升力系数分布规律均存在很大差异;静气弹变形使得连结翼升力线斜率增大4.3%,纵向静稳定性导数增大145.8%,但会带来较大的低头力矩增量;与单独前翼对比表明,连结翼后翼大大限制了前翼的负扭转变形,使得升力损失降低为单独前翼的21%;与单独后翼对比表明,连结翼前翼大大限制了后翼的正扭转变形,降低了后翼扭转发散的风险;研究结果揭示了连结翼布局特殊的静气动弹性特性,对连结翼的气动/结构设计具有一定的工程指导价值。
关键词:连结翼;静气动弹性;松耦合;扭转变形;展向升力分布;纵向静稳定;扭转发散
按照Wolkovitch[1]的定义,连结翼布局飞行器是指机翼包含串列的前翼和后翼,从正视图和侧视图看均为菱形,通常后翼的根部与垂尾的顶端相连,前后翼的连结点位置根据设计要求有比较大的选择灵活性。与常规布局飞机相比,连结翼具有众多的优点,在气动方面,具有低的诱导阻力,高的最大配平升力系数,以及良好的跨音速面积分布;在结构方面,可以保证较低的结构重量和较高的结构刚度;从飞行力学角度看,具有良好的稳定性和操纵性,可以使用直接升力控制和直接侧力控制。因此,连结翼布局具有广阔的发展空间和应用前景。
对于连结翼布局的气动弹性研究,国外开展了大量的计算工作,E Livne[2]对连结翼布局气动弹性方面的已有研究进行了详细总结,并提出了未来研究面临的挑战。国内相关研究工作还相对较少,郑诚行等[3]对连结翼发生静气弹变形后的气动特性和静气弹发散特性进行了计算,指出连结翼的发散速压要大大高于翼尖不连接时。张波成等[4]在相同总体条件下,对设计出的传统布局机翼和连结翼进行了气动弹性计算,指出在等效的气动载荷作用下,连结翼具有更小的弯曲和扭转变形,并且颤振速度也要高于传统布局机翼。
然而,上述研究中的气动结构模型往往比较简化,如气动力求解采用面元法,结构采用梁模型。随着计算机技术的进步,耦合计算流体力学(CFD)和计算结构动力学(CSD)求解气动弹性问题的方法获得了快速发展[5]。CFD/CSD耦合可以获得任意时刻的非定常气动力和结构响应,并且可以考虑各种非线性因素。本文以某连结翼布局为对象,采用松耦合方式,耦合CFD和CSD求解技术,计算分析了连结翼的静气弹变形特性和展向升力分布特性;并研究了静气弹效应对连结翼纵向气动特性的影响;最后与单独前翼和单独后翼进行了静气弹特性的对比研究。
1计算方法
气动力计算模块使用FLUENT软件,采用有限体积法求解非定常雷诺平均N-S方程,空间离散采用Roe格式,时间离散方法为隐式双时间推进格式,湍流模型选取k-ωSST。
结构方面使用ABAQUS隐式动力学模块求解式(1)表示的结构动力学方程来获得时域内的结构位移响应,数值求解采用HHT直接积分方法。

(1)
目前,CFD/CSD耦合主要发展了3种方法:全耦合、紧耦合和松耦合。全耦合[6]方式将流体和结构方程组重构整合为一套新的方程组,随时间推进同时进行求解,然而由于流体和结构物理特性的巨大差异,很难用统一的数值方法对方程组进行求解,目前一般局限于二维问题的研究,难以用于工程实际。松耦合[7]方式保持了气动模块和结构模块的独立性,通过数据交换模块将两者进行耦合,交错时间进行推进求解,在选择气动和结构各自的求解器时有较大灵活性,可以充分利用现存的大量成熟的流体和结构求解器;松耦合的缺点是存在时间滞后问题,时间精度只有一阶,而对于本文静气弹问题的求解,只关心最终的静气弹收敛结果,并不要求精确的时域响应历程,因此本文采用松耦合方式,计算流程如图1所示。

图1 松耦合计算流程
采用松耦合方式在时域内求解气动弹性问题时,每个时间步内,结构发生变形后需要将耦合面的结构位移反馈给气动网格,作为非定常气动力求解的运动边界条件,气动模块则需要将气动载荷传递给结构耦合界面,作为结构求解的力边界条件。通常气动和结构网格不重合,两者的网格划分依据存在较大的差异,因此需要进行插值来完成气动结构间的数据交换,本文采用多场耦合工具MPCCI作为数据交换模块。
气动表面网格根据结构变形发生移动后,空间网格也要随之调整,本文采用弹簧网格法[8]和局部重构方法[9]相结合的方式完成空间网格的变形,即在结构变形量较小时,使用弹簧网格法;在结构发生大变形时出现空间网格畸变严重的情况下,采用局部重构方法来剔除变形后质量较差的网格,重新生成质量较高的网格。
2计算模型
连结翼模型三视图如图2所示,由前翼、后翼和翼尖连接端板组成,前翼无上反角水平放置,后翼带有下反角,前后翼通过翼尖处的端板连接,前翼后掠角为30°,后翼前掠角为30°,前后翼的弦长、展长和采用的翼型均相同。
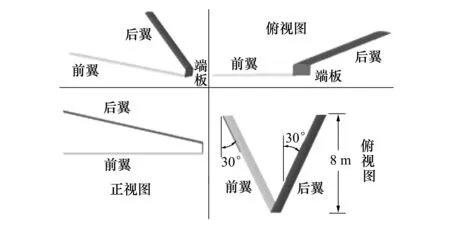
图2 连接翼三视图
气动计算采用四面体非结构网格,空间体网格数量329万,物面网格数量18万,对称面网格局部示意图如图3。计算来流参数选取海拔高度H=10km,马赫数M=0.3, 迎角α=0°~6°。
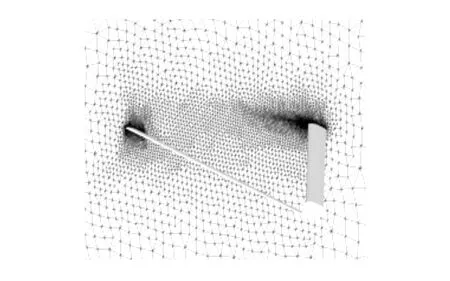
图3 对称面气动网格示意图
图4为连结翼内部结构布置图,包括翼肋、前梁、后梁和蒙皮。前翼的结构布置、材料属性与后翼完全一致,但后翼的蒙皮厚度要大于前翼。翼尖连接端板采用厚钢板进行模拟,目的是保证连接端板具有足够的结构刚度。边界条件为前翼和后翼在翼根处固支。

图4 连结翼内部结构布置
3计算结果分析
3.1迎角α=4°时连结翼静气弹特性
首先分析连结翼在典型迎角α=4°时的静气动弹性特性。发生静气弹变形后,前翼和后翼沿展向的弯曲及扭转变形分布如图5和图6所示。可以看出,前翼沿展向主要发生负扭转变形,后翼沿展向发生正扭转变形,前翼和后翼从翼根到翼尖的扭转变形量均是先增大后减小。受翼尖处端板的作用,前翼和后翼的弯曲及扭转变形在翼尖处基本达到一致。
连结翼静气弹变形前后的升力比较如表1所示。可以看出,静气弹变形后连结翼总升力(Ltotal)略微增大,而前翼升力(Lfront)发生较大幅度下降,降幅达6.5%,后翼升力(Lrear)发生较大幅度增加,增幅达15.5%。这与连结翼发生的扭转变形是对应的,前翼发生负扭转变形,导致前翼的当地迎角降低,因此带来升力损失;后翼发生正扭转变形,提高了后翼的当地迎角,因此带来升力增量。

表1 迎角α=4°时静气弹变形前后升力比较
图7为连结翼前翼和后翼静气弹变形前后的展向升力系数分布比较。可以看出,发生静气弹变形后,前翼展向升力系数分布曲线整体下移,后翼整体上移,与表1的结论是一致的,即前翼卸载,后翼加载,这表明静气弹变形对前翼的结构设计是有利的,而对后翼的结构设计是不利的,在结构设计时需要注意这一点。同时可看出,沿展向前翼的升力损失和后翼的升力增量,从翼根到翼尖均是先增大后减小,这是由于前翼和后翼的扭转变形量从翼根到翼尖均是先增大后减小。此外,无论是刚体构型还是静气弹变形后,前翼的展向升力分布规律与后翼存在很大不同,前翼从翼根到翼尖先增大后减小,但变化幅度相对较和缓,而后翼沿展向则单调下降,且下降较快,幅度也较大,这主要与连结翼前翼为后掠,后翼为前掠的气动布局特性有关。

图5 迎角α=4°时展向弯曲变形分布 图6 迎角α=4°时展向扭转变形分布 图7 静气弹变形前后展向升力分布比较
3.2静气弹变形对气动特性的影响
连结翼发生静气弹变形前后的升力系数CL随迎角变化如图8所示。从连结翼总升力系数曲线看,静气弹变形后的升力线斜率要大于刚体构型,并且各个迎角下的升力系数也要大于刚体构型,因此,在所计算的迎角范围内,静气弹变形对连结翼总升力特性是有利的;从前翼升力系数曲线看,静气弹变形后曲线整体下移,表明在各个迎角下前翼均发生了升力损失,这与前翼发生负扭转变形有关;从后翼升力系数曲线看,静气弹变形后曲线整体上移,表明在各个迎角下后翼的升力均增加,这与后翼发生正扭转变形有关。

图8 静气弹变形前后升力系数CL比较
静气弹变形前后,连结翼的俯仰力矩系数Cm随迎角变化如图9所示。可以看出,在各个迎角下,连结翼发生静气弹变形后,带来较大的低头力矩增量,这是由于连结翼前翼发生负扭转变形,后翼发生正扭转变形,导致前翼升力减小,后翼升力增加,合力作用点后移,因此带来较大的低头力矩增量。此外,纵向静稳定导数|Cmα|增大,表明静气弹变形使得连结翼焦点后移,因此对纵向静稳定性是有利的。
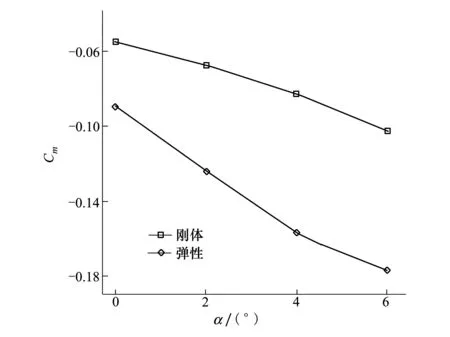
图9 静气弹变形前后俯仰力矩系数系数Cm比较
3.3单独前翼静气弹特性比较
将连结翼的前翼分离出来,对单独前翼进行静气弹计算,并与连结翼前翼进行对比。单独前翼的气动外形及结构参数与连结翼前翼完全一致,选取来流迎角α=4°进行比较研究。
静气弹变形后,连结翼前翼和单独前翼的展向扭转变形比较如图10所示。可以看出,连结翼后翼的存在大大降低了前翼的负扭转变形量,并且改变了展向变形分布规律。连结翼前翼的扭转变形量沿展向先增大后减小,最大负扭转角为-1.04°,约在连结翼前翼40%展长处取得;而单独前翼的扭转变形量沿展向则一直单调增加,最大负扭转角达-3.4°,在翼尖处取得,这符合后掠翼的静气弹变形规律,后掠翼存在弯扭耦合效应,即弯曲变形会带来负扭转变形,因此后掠翼的负扭转变形通常更为严重。

图10 迎角α=4°时扭转变形沿展向分布比较
静气弹变形前后,连结翼前翼和单独前翼展向升力系数分布比较如图11所示。

图11 迎角α=4°时静气弹变形前后展向升力分布比较
对于刚体构型,连结翼前翼的展向升力系数整体高于单独前翼,可见后翼的存在提高了前翼的升力;此外,连结翼的翼尖端板起到了类似翼梢小翼的作用,因此连结翼前翼的升力系数在翼尖处下降比较和缓,而单独前翼在翼尖处则下降较快。静气弹变形后,单独前翼的升力损失比连结翼前翼严重得多,这与两者的负扭转变形是对应的。此外,连接翼前翼的最大负扭转变形在展向中部取得,到翼尖处变为正扭转,因此连结翼前翼在展向中部的升力系数损失较大,在翼尖处升力系数则略大于刚体构型。
静气弹变形前后,连结翼前翼(LJW-front)和单独前翼(Lsingle-front)的升力比较如表2所示。可以看出,静气弹变形后两者的升力均发生损失,但连结翼前翼损失仅6.5%,单独前翼损失则高达32.8%,大大高于连结翼前翼。此外,静气弹变形后,连结翼后翼会产生升力增量,从而弥补了前翼的升力损失,因此连结翼的总升力反而增大。可见单独后掠翼静气弹变形后的升力损失是一个值得关注的问题,这与后掠翼的弯扭耦合效应有关,结构设计时通常需要保证机翼有足够的刚度来限制静气弹变形,而这将带来较大的结构重量。
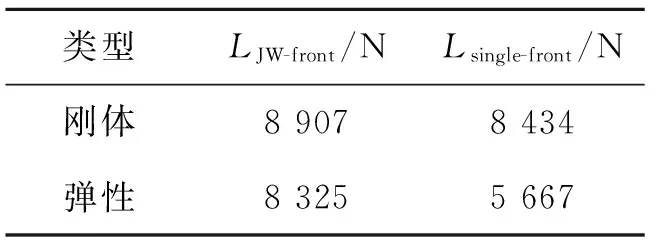
表2 连结翼前翼和单独前翼升力比较
3.4单独后翼静气弹特性比较
将连结翼的后翼分离出来,对单独后翼进行静气弹计算,并与连结翼后翼进行对比。单独后翼的气动外形和结构参数与连结翼后翼完全一致,选取来流迎角α=4°进行比较研究。
静气弹变形后,连结翼后翼和单独后翼的扭转变形比较如图12所示。
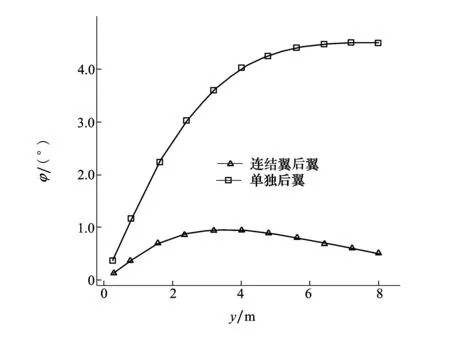
图12 迎角α=4°时扭转变形沿展向分布比较
可以看出,连结翼后翼和单独后翼均发生正扭转变形,但连结翼后翼最大扭转角为0.95°,在连结翼后翼展向40%处取得,单独后翼最大扭转角则增至4.5°,在翼尖处取得,远远高于连结翼后翼,表现出单独前掠翼易于扭转发散的特点。因此连结翼前翼的存在大大抑制了后翼的静气弹变形,降低了单独后翼发生扭转发散的风险。
静气弹变形前后,连结翼后翼和单独后翼的升力比较如表3。可以看出,静气弹变形后两者的升力均增加,但连结翼后翼升力增幅为15.5%,而单独后翼增幅则达到47.9%。虽然单独后翼静气弹变形会带来更大的升力增量,但却存在扭转发散速度低的问题,从而限制了前掠翼飞行性能的发挥,而连结翼由于前翼对后翼正扭转变形的限制,在一定程度上降低了后翼扭转发散的风险。
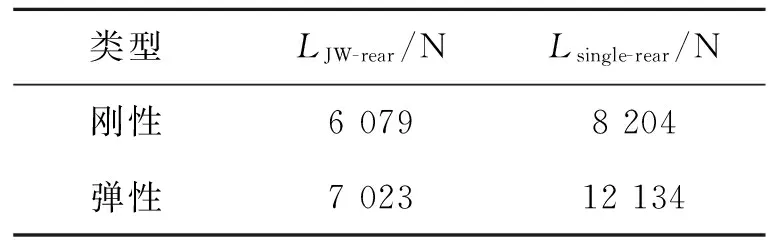
表3 连结翼后翼和单独后翼升力比较
4结论
本文基于CFD/CSD松耦合求解技术,对连结翼的静气动弹性进行了计算研究,主要结论如下:
1) 静气弹变形后,前翼负扭转,升力损失,后翼正扭转,升力增加,这对前翼的结构设计是有利的,而对后翼是不利的,在这类布局的结构设计时需要着重注意。
2) 发生静气弹变形后,连结翼总升力略微增加,升力线斜率增大4.3%,纵向静稳定性导数增大145.8%,但带来较大的低头力矩。
3) 与单独前翼静气弹计算对比,表明连结翼后翼大大限制了前翼的负扭转变形,使得连结翼前翼的升力损失降低为单独前翼的21%。
4) 与单独后翼静气弹计算对比,表明连结翼前翼大大限制了后翼的正扭转变形,降低了后翼扭转发散的风险。
参考文献:
[1]Wolkvitch J. The Joined Wing: An Overview[J]. Journal of Aircraft, 1986, 23(3): 161-178
[2]Livne E. Aeroelasticity of Joined-Wing Airplane Configurations: Past Work and Future Challenges-A Survey[R]. AIAA-2001-1370
[3]郑诚行,肖小玲. 翼尖连接机翼布局弹性气动力探讨[J]. 空气动力学学报, 2005, 23(1): 93-96
Zheng Chengxing, Xiao Xiaoling. The Exploration of Elastic Aerodynamics for a Joined Wing Configuration[J]. Acta Aerodynamica Sinica, 2005, 23(1): 93-96 (in Chinese)
[4]张波成,万志强,杨超. 连翼布局飞行器飞行载荷与颤振分析[J]. 工程力学, 2010, 27(8): 229-233
Zhang Bocheng, Wan Zhiqiang, Yangchao. Flight Loads and Flutter Analysis of the Joined Wing Aircraft[J]. Engineering Mechanics, 2010, 27(8): 229-233 (in Chinese)
[5]安效民,徐敏,陈士橹. 多场耦合求解非线性气动弹性的研究综述[J]. 力学进展, 2009, 39(3): 284-298
An Xiaomin, Xu Min, Chen Shilu. An Overview of CFD/CSD Coupled Solution for Nonlinear Aeroelasticity[J]. Advances in Mechanics, 2009, 39(3): 284-298 (in Chinese)
[6]Tienne S, Pelletier D, Garon A. A Monolithic Formulation for Steady-State Fluid-Structure Interaction Problems[R]. AIAA-2004-2239
[7]Hurka J, Ballmann J. Elastic Panels in Transonic Flow[R]. AIAA-2001-2722
[8]Blom F J. Considerations on the Spring Analogy[J]. Int J Numer Meth Fluids, 2000, 32: 647-668
[9]Batan J D, Lhner R. Numerical Simulation of Pilot/Seat Ejection From an F-16[R]. AIAA-1993-0783
收稿日期:2016-03-15
基金项目:民机专项(MIZ-2015-F-009)、陕西省科技统筹项目(2015KTCQ01-78)资助
作者简介:张强(1991—),西北工业大学硕士研究生,主要从事无人机气动弹性研究。
中图分类号:V211.47
文献标志码:A
文章编号:1000-2758(2016)03-0437-06
Numerical Research on Static Aeroelasticity of Joined Wing Based on CFD/CSD Coupling
Zhang Qiang1,2, Zhu Xiaoping2, Zhou Zhou1,2, Wang Wei1,2
1. College of Aeronautics,Northwestern Polytechnical University,Xi'an 710072,China2. Science and Technology on UAV Laboratory,Northwestern Polytechnical University,Xi'an 710065, China
Abstract:With a joined wing configuration UAV as the study object, static aeroelasticity was numerically investigated by coupling CFD and CSD using loosely-coupled algorithm. CFD module adopts unsteady Reynolds Averaging N-S equations and CSD module adopts direct integration method to solve structural dynamic equation. Advancing solution in time domain, the static aeroelastic results are then obtained after convergence. Research shows that after static aeroelastic deformation of joined wing, the front wing twists negatively while the rear wing positively; the lift of front wing decreases while rear wing increases; the spanwise lift coefficient distribution differs greatly between front wing and rear wing; after static aeroelastic deformation, the lift curve slope and the longitudinal static stability derivative both increase, but large increment of nose down moment is produced; compared to single front wing, rear wing of joined wing restricts the deformation of front wing largely, leading to the loss of lift far less than single front wing; compared to single rear wing, front wing of joined wing restricts the positive torsional deformation of rear wing largely, which reduces the risk of divergence of rear wing. The results revealed the particular aeroelastic characteristics of joined wing configuration, which is to be of certain value to the aerodynamic and structural design of joined wing.
Keywords:joined wing; static aeroelastic; loosely couple; twist deformation; spanwise lift distribution; lift curve slope; longitudinal static stability; divergence

