基于泛逻辑的泛容差关系的研究

刘城霞, 何华灿, 张仰森, 朱敏玲

1.北京邮电大学 计算机学院, 北京　100876; 2.北京信息科技大学, 北京　100101 3.西北工业大学, 陕西 西安　710072



基于泛逻辑的泛容差关系的研究

刘城霞1,2, 何华灿1,3, 张仰森2, 朱敏玲2

1.北京邮电大学 计算机学院, 北京100876; 2.北京信息科技大学, 北京100101 3.西北工业大学, 陕西 西安710072

摘要：粗糙集是用确定的方法处理不确定信息和数据，但它要求属性信息是离散的,而且针对的是完备信息系统。而泛逻辑是研究人工智能领域中的不确定性、不完全性以及模糊性，它针对的信息可以是离散的，也可以是连续的。针对不完备信息系统扩展泛逻辑中的泛等价关系，得到泛容差关系，并对连续或离散的属性取值应用泛容差关系进行分类，代替原来的扩展粗糙集中的容差关系，定义新的相似度的计算方法，进而进行数据填充，最后用实例进行了应用说明。

关键词：粗糙集；泛逻辑；容差关系；泛容差关系

粗糙集理论[1]在1982 年由波兰数学家Pawlak提出的一种处理不精确、不确定和模糊数据的数学工具，它能有效地从数据本身提供的信息中发现有效、潜在的知识。近年来该理论成功地在机器学习、数据挖掘、智能数据分析等领域得到了广泛应用，受到了众多学者的重视，取得了很大的发展。

泛逻辑理论[2]是本世纪初由何华灿教授提出的，它是针对人工智能等领域中传统逻辑无法解决的问题而开展的。它是在二值逻辑、多值逻辑和模糊逻辑的基础上，研究人工智能领域中的不确定性、不完全性以及模糊性的一种柔性逻辑。其中对命题的真值域、命题连接词、量词等都进行了柔性化，可以全面反映命题真值的不确定性、真值误差的不确定性、命题之间相关关系的不确定性等，使之更适合于现实世界的推理规则。泛逻辑和粗糙集都适用于处理不精确、不确定的信息，而这也给二者的结合带来了可行性与便利性。

1粗糙集理论基础及其扩充

1.1完备信息系统下的粗糙集理论基础

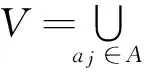
(1)若∀aj∈C使得V中不含空值,即f(xi,aj)≠φ,则称S是完备信息系统,即所处理的信息表是完备的,每个样本对象的所有属性值都是已知的。粗糙集理论正是基于完备信息系统这样一个假设。

为便于数学推导,粗糙集中通常用等价关系代替分类。定义R代表论域U上的一种关系,它可以是一种属性的描述,也可以是一个属性集合的描述。在一般叙述中,R 等价关系和R属性都是同一概念。在属性约简中,把任意非空属性子集看做是关系R。任取非空属性子集R⊆A,如果xi,xj∈U,∀ak∈R,f(xi,ak)=f(xj,ak)均成立,则称xi,xj关于R不可分辨,R为不可分辨关系,记为IND(R)。IND(R)即可把论域U中的元素分为若干个等价类,全体等价类的集合记为U/IND(R)。

给定信息系统S=(U,A,V,F),∀X⊆U和等价关系R,则X关于R的下近似和上近似分别定义如下:

下近似

(2)上近似

(3)式中，[x]R表示的是包含元素x∈U的R等价类。

根据上、下近似的定义给出边界域、正域和负域的概念如下：

BNDR(X)=R-(X)-R-(X) 称为X的R边界域。

POSR(X)=R-(X) 称为X的R正域。

NEGR(X)=U-R-(X) 称为X的R负域。

由上述定义可知下近似R-(X)和正域POSR(X)表示在知识R下论域U中确定属于集合X的对象集,上近似R-(X)表示在知识R下论域U中可能属于集合X的对象集,所以边界域BNDR是在知识R不能确定是否属于集合X的对象集,负域NEGR(X)则表示在知识R下论域U中与集合X无关的对象集。

1.2不完备信息系统中扩充粗糙集模型的容差关系及量化容差关系

粗糙集理论是基于完备信息系统的,当信息系统不完备时,需要进行数据补齐或对粗糙集模型进行扩充。数据补齐主要采用某种方法(通常是概率统计)对所有未知属性值进行填补,将不完备信息系统转化为完备信息系统,然后用经典粗糙集理论来处理。比如现有的c4.5、删除法、最大频率法等[3]。数据补齐法应用起来十分简便,但它是对原始信息系统中未知属性值的一种人为估计,对原始信息系统的信息有不同程度的扰动,不能反映原始系统的真实情况,获得的知识可用性差。模型扩展主要是将经典粗糙集理论中的不可分辨关系这一等价关系扩充为非等价关系,直接处理不完备信息系统。比如Kryszkiewicz提出容差关系[4],Stefanowski等人提出的非对称相似关系[5],Stefanowski等人提出的量化容差关系[6],王国胤等人提出的限制容差关系[7],Grzymala-Buss提出的特征关系[8]等,都是对粗糙集运算模型的扩充。文献[9]对不完备系统的粗糙集扩充方法进行了总结和研究。

1.2.1容差关系

当不完备信息系统S中所有未知属性值是遗漏型时,对属非空属性子集B⊆A,M.Kryszkiewicz提出了如下容差关系

(4)

对任意对象x∈U的容差类

(5)

对象子集X⊆U的下近似和上近似分别为

(6)

(7)

容差关系满足自反性和对称性,但不一定满足传递性。

1.2.2量化容差关系

对于不完备信息系统中的个体, 由于已知信息的不同, 也可以根据已知信息的相同程度来刻画它们之间的相近似程度。 据此,Stefanowski等人提出了基于量化容差关系的扩充Rough集模型。

在不完备信息系统S中,∀b∈A记

(8)

若U中对象对每个属性的取值独立且均匀分布,则任意对象∀x,y∈U关于属性子集的相似度可定义为

(9)

容差关系所描述的样本对象之间相似度的取值范围是{0,1},Ⅰ型量化容差关系虽然将样本对象相似度的取值范围扩充到了[0,1],但需要知道属性取值的概率分布等相关知识。

量化容差关系还有不同的改进模型,在文献[10]中,定义了改进的量化容差关系。

(10)

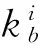
2泛逻辑理论基础

本文第二作者为了探索逻辑的一般规律,提出建立能包容各种逻辑形态和推理模式的泛逻辑学理论。泛逻辑学针对现代逻辑中存在的缺陷,基于三角范数理论,利用广义相关性和广义自相关性将逻辑关系定义为一组连续可变的算子簇,并提出了和如何使用该算子簇中的算子,真正实现了模糊逻辑关系的柔性化。这里为简化计算,先不考虑广义自相关性,只考虑广义相关性,那么用到的零级泛逻辑理论。

1) 零级泛与及泛或

经过多年的发展,现在普遍认同的是以T范数表示逻辑与,以T余范数S表示逻辑或。T范数和S范数是是泛逻辑学研究泛与/或运算的数学基础。用h表示的是广义相关性,对零级不确定性问题, 用2个仅受h控制的函数F0(x,h)=xm和G0(x,h)=1-(1-x)m作为零级T性生成元完整簇和零级S性生成元完整簇,把它们带入泛与何泛或运算的基模型分别生成的零级T范数完整簇T(x,y,h)和零级S范数完整簇S(x,y,h)如下

(11)

(12)

式中

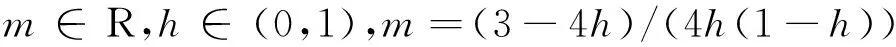
由于广义相关系数h是连续变化的,因此会有无限多个连续的T(x,y,h)算子和S(x,y,h)算子。

2) 零级泛蕴含与泛等价

由零级T性生成元完整簇F0(x,h)=xm代入蕴含运算的基模型生成零级I范数完整簇

(13)

记作由零级T性生成元完整簇F0(x,h)=xm代入等价运算的基模型生成零级I范数完整簇

(14)

记作↔h。

其中h>0.75为+,否则为-,m=(3-4h)/

(4h(1-h)),h=(1+m)-((1+m)2-3m)1/2)

/(2m)。

它有的4个特殊算子是:

最小等价,又称Zadeh等价Q(x,y,1)=Q3=ite{1|x=y;min(x,y)}

(15)

中极等价,又称概率等价Q(x,y,0.75)=Q2=min(x/y,y/x)

(16)

(Ⅰ等价)

中心等价,又称有界等价

(17)

最大等价又称突变等价Q(x,y,0)=Q0=ite{x|y=1;y|x=1;1}

(18)

3泛容差关系与相似度计算

在完备系统不可分辨关系定义中要求xi,xj∈U,∀ak∈R,f(xi,ak)=f(xj,ak)均成立,这个定义适合离散型属性,对于连续型的属性,一般的做法是先将其离散化,然后再使用不可分辨关系进行等价类的划分。然而,离散化的算法、精度都会影响分类的效率和准确性,进而影响属性约简的效率。如果能直接对连续属性进行不可分辨关系的分类,就可以避免人为离散化引起的取值误差,而且可以省略离散化过程,提高效率和精度。

完备信息系统中可以用泛逻辑的泛等价关系

(19)

来作为不可分辨关系,则当Qb(x,y,h)>1-α时认为等价,其中α为阀值,否则不等价。其中

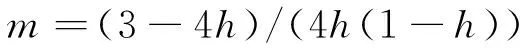
这里h为广义相关系数,可以在使用时根据实际需要进行调整。在多数情况下系统中用到的是相容相关,即h∈[0.5,1],文中案例也是相容相关情况的实例。xi,k,xj,k代表xi,xj的属性ak的值。利用该泛等价关系处理离散属性时和原等价关系一致,连续属性可以直接处理而不需要进行离散化,有关该泛等价的性质及证明在另外的文章中有详细论述。

3.1泛容差关系

当信息系统不完备时,所有未知属性值是遗漏型时,对属非空属性子集B⊆A,定义泛容差关系

(20)

对任意对象x∈U的容差类

(21)

对象子集X⊆U的下近似和上近似分别为

(22)

(23)

泛容差关系满足自反性和对称性,但不一定满足传递性。

对于泛容差关系,可以对其进行量化,参考1.2.2中量化容差关系的定义,定义泛容差关系的量化方法

(24)

式中，N(bj±ba)代表的是属性b取值在bj±ba范围内的对象个数,如为离散属性,则为属性b取值等于bj的对象个数,bα为满足Qb(x,y,h)>(1-α)的该属性的阀值。N表示所有在属性b上有值的对象的个数,Nbi表示对属性b分类后每类的对象个数,b为离散属性时即为属性b取值等于bi,i=1,…,m的对象个数,b为连续属性时即为属性b取值分类每类的对象个数。

性质1当属性全部为离散值时,泛容差关系TQB相当于容差关系；

性质1证明当属性全部为离散值时,泛容差关系TQB相当于容差关系。

即当属性全部为离散值时,泛容差关系TQB中Qb(x,y,h)>1-α等价于b(x)=b(y)。

显然,当b(x)=b(y)时,Qb(x,y,h)=1>1-α成立。

当Qb(x,y,h)>1-α即

以h=0.5为例,此时m=1

当属性离散时,令阀值α取值小于任意2个属性值之差,则|b(x)-b(y)|<α时b(x)=b(y)。

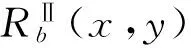
3.2实例分析

现以某医院有关流感诊断的原始数据信息表S0=(U,A,V,F)为例,进行对比分析。论域U={x1,x2,x3,x4,x5,x6,x7,x8,x9},属性集合A={a1,a2,a3,a4,d}分别代表肌肉酸痛、咳嗽、头痛、体温和决策属性是否为流感,a1,a2,a3取值集合为{0,1,2,3},分别代表{无症状,轻微,较严重,严重),a4取值集合为连续型数据,取值范围[35,40],d为决策属性,取值集合为{0,1,2}分别代表{不是,疑似,是}。“*”表示遗漏值。

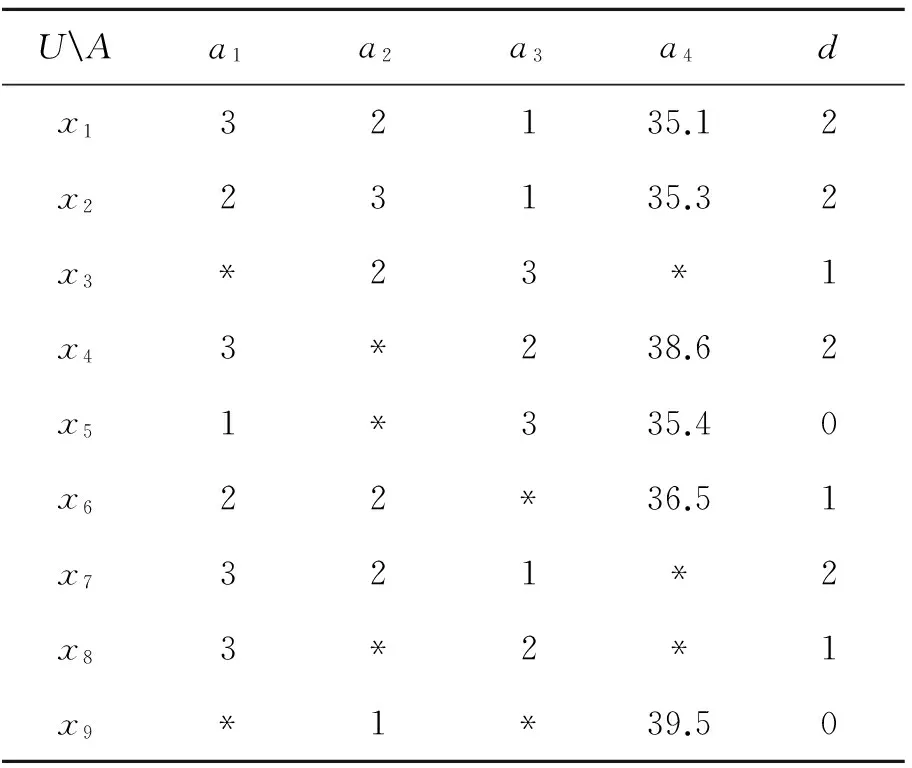
表1　连续型不完备信息系统表S0

对体温属性进行离散化,[35,36.25)离散化为0,[36.25,37.5)离散化为1,[37.5,38.75)离散化为2,[38.75,40]离散化为3,离散化后取值{0,1,2,3},分别代表{偏低,正常,偏高,高}。

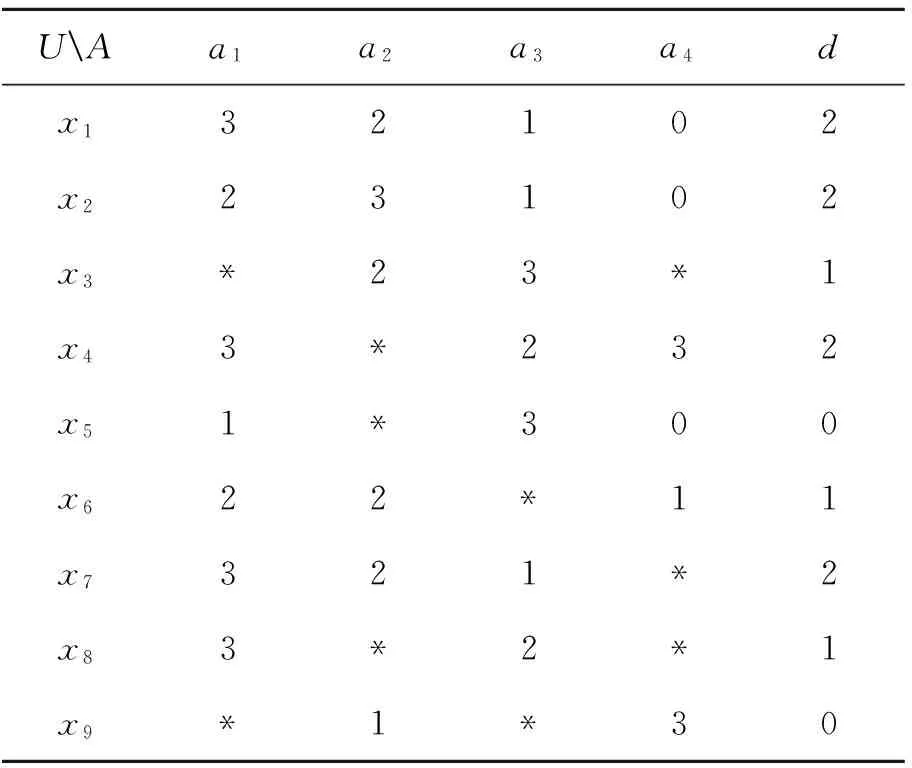
表2　离散化后的不完备信息系统表S0

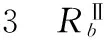
表量化容差矩阵TⅡ

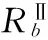
表4　根据量化容差矩阵TⅡ进行补齐后的信息表SⅡb

由于TⅡ中对象间相似度都不同,所以取相似度大的进行补齐,得到了完备信息系统SⅡ。

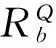
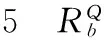
表量化容差矩阵Th

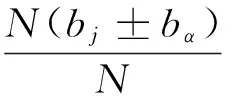
x4,xg2个对象的相似度

表6　根据量化容差矩阵Th进行补齐后的信息表Sh

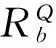
4结论

应用粗糙集理论指导数据挖掘已经应用非常广泛,但粗糙集有自身的局限性。比如必须要使用离散型数据,必须是完备系统等。本文从对理论扩展的角度,针对不完备系统应用泛容差对容差关系进行了重新定义,使之可以针对连续型数据进行划分,是对不完备系统下粗糙集运算模型的扩展。

参考文献：

[1]Pawlak Z. Rough Sets[J]. International Journal of Computer and Information Science, 1982,11(5): 341-356

[2]何华灿. 泛逻辑学原理[M]. 北京：科学出版社，2001

He Huacan. The Theory of Universal Logic[M]. Beijing, Science Press, 2001 (in Chinese)

[3]Grzylama-Busse J W, Hu M. A Comparison of Several Approaches to Missing Attribute Values in Data Mining[C]∥Proceedings of the Second International Conference on Rough Sets and Current Trends in Conlputing RSCTC 2000, Banf, Canada, Springer Berlin, 2000: 340-347

[4]Kryszkiewicz M. Rough Set Approach to Incomplete Information Systems[J]. Information Sciences, 1998, 112: 39-49

[5]Stefanowski J, Tsoukias A. Incomplete Information Tables and Rough Classification[J]. Computational Intelligence, 2001, 17(3): 545-566

[6]Stefanowski J, Tsoukias A. Valued Tolerance and Decision Rules[C]∥Volume 2005 of Lecture Notes in Artificial Intelligence Berlin, Springer, 2001: 212-219

[7]王国胤. Rough集理论在不完备信息系统中的扩充[J]. 计算机研究与发展, 2002, 39(10): 1238-1243

Wang Guoyin. Extension of Rough Set Under Incomplete Information System[J]. Journal of Computer Research and Development, 2002, 39(10): 1238-1243 (in Chinese)

[8]Grzymala-Busse J W. Rough Set Strategies to Data with Missing Attribute Values[C]∥The 3rd International Conference on Data Mining. Melbourne，FL，USA, 2003: 56-63

[9]官礼和. 基于粗糙集理论的不完备信息处理方法研究[J]. 重庆邮电大学学报，2009,21(4)：461-466

Guan Lihe. Processing Incomplete Information Methods Based on Rough Set[J]. Journal of Chongqing University of Posts and Telecommunications, 2009, 21(4): 461-466 (in Chinese)

[10] 邓耀进, 李仁发. 一种粗糙集理论中量化容差关系的改进[J]. 计算机工程与科学，2009, 31(10): 105-108

Deng Yaojin, Li Renfa. An Improvement on the Valued Tolerance Relation in the Rough Set Theory[J]. Computer Engineering & Science, 2009, 31(10): 105-108 (in Chinese)

[11] Gao Yuqin, Fang Guohua, Liu Yaqin.θ-Improved Limited Tolerance Relation Model of Incomplete Information System for Evaluation of Water Conservancy Project Management Modernization[J]. Water Science and Engineering, 2013, 6(4): 469-477

收稿日期：2015-10-27

基金项目：“促进高校内涵发展-专业建设-面向大类人才培养模式的2016专业培养方案修订”项目资助

作者简介：刘城霞(1978—)，女，北京邮电大学博士研究生，主要从事数据挖掘、粗糙集及泛逻辑的研究。

中图分类号：TP301.6

文献标志码：A

文章编号:1000-2758(2016)03-0473-07

The Study of Universal Tolerance Relation Based on Universal Logic

Liu Chengxia1,2, He Huacan1,3, Zhang Yangsen2, Zhu Minling2

1.Computer School, Beijing University of Posts and Telecommunications, Beijing 100876, China 2.Beijing Information and Technology University, Beijing 100101, China 3.Northwestern Polytechnical University, Xi′an 710072, China

Abstract:Rough set theory can be used to deal with the imprecise data and information by certain method but its basis is that the attribute′s value must be discrete and the system must be complete .Universal logic can do with the uncertain, incomplete and fuzzy information in artificial intelligence and the data can be discrete or continuous. Use the universal logic to redefine the tolerance relation and use universal tolerance relation to classify the continuous or discrete attribute, we can extend the scope of application of rough set theory and universal logic. This paper makes focus on the new concept of universal tolerance relation and new computation method of similarity between objects and then we can complete the data based on this. At last an example is given to illustrate it.

Keywords:rough set; universal logic; tolerance relation; universal tolerance relation