基于高阶格式的旋转类问题非定常流动数值模拟研究
付炜嘉, 李杰, 娄琪琳
(西北工业大学 航空学院, 陕西 西安 710072)
基于高阶格式的旋转类问题非定常流动数值模拟研究
付炜嘉, 李杰, 娄琪琳
(西北工业大学 航空学院, 陕西 西安710072)
摘要:基于结构网格动态面搭接技术、五阶Roe-WENO格式求解非定常RANS方程,开发了用于旋转类问题非定常流动数值模拟的计算分析程序,并针对典型旋转类算例进行了分析验证。对Caradonna-Tung旋翼的计算结果表明:计算得到的旋翼桨叶表面压力分布与实验值吻合良好,计算程序可以用于旋翼悬停、简单前飞状态的气动力数值模拟与分析;同时在计算网格分布相同情况下,五阶Roe-WENO格式较三阶Roe-MUSCL格式对于旋翼尾迹的分辨率更高,计算得到的旋翼桨尖涡尾迹更加清晰。对螺旋桨机翼干扰问题的研究结果表明,所开发的计算程序对于刚性旋转类问题非定常流动数值模拟具有很好的适用性,对于尾迹的捕捉具有较高的精度,满足工程实际应用的要求。
关键词:结构网格动态面搭接技术;五阶Roe-WENO格式;旋翼;螺旋桨;非定常流动
当前,计算流体力学(CFD)技术已经成为空气动力学问题研究的主要手段,被广泛地用于工程实际问题的计算分析。旋转类问题非定常流动数值模拟一直是空气动力学研究的难点与热点,其难点主要包括以下2个方面:①如何采用合理的网格技术实现旋转运动;②如何提高尾迹模拟的精度。
旋转类问题在工程中随处可见,包括直升机旋翼、螺旋桨、风力机叶片、航空发动机叶片等问题。目前,研究者大多通过求解雷诺平均N-S方程对这类问题进行数值模拟研究[1-4]。从国内外有关旋转类问题非定常流动数值模拟研究文献来看,大致有2种研究倾向:①比较侧重于旋转物体本身的气动力数值模拟分析,例如旋翼桨叶、螺旋桨桨叶和风力机叶片的表面载荷分布及其相关力系数的计算。②比较侧重于旋转物体尾迹的高精度数值模拟,通过对数值方法的改进完善来提高尾迹涡模拟的模拟精度,捕捉到更多的流动细节。后者逐渐成为旋转类问题非定常流动数值模拟发展趋势,对于螺旋桨问题,螺旋桨的尾迹的模拟精度对于螺旋桨滑流与机翼或飞机其他部件的气动干扰研究有重要的意义。对于旋翼问题,旋翼桨尖涡的模拟精度对于深入研究旋翼绕流机理、桨涡干扰、旋翼机身干扰以及旋翼气动噪声预测至关重要[5]。由此可见,有必要发展一套适用于旋转问题的非定常高精度数值模拟研究的计算分析程序。
本文采用结构网格动态面搭接技术实现物体的旋转,基于五阶Roe-WENO格式和非定常RANS方程,开发了一套用于旋转类问题非定常流动数值模拟研究的计算分析程序,并针对旋翼和螺旋桨等典型算例进行计算分析来验证该计算程序的可靠性。
1数值计算方法
1.1控制方程
本文对旋转类问题流场的数值模拟是基于惯性笛卡尔坐标系开展的,在惯性笛卡尔坐标下,积分形式的非定常N-S方程组可写作:
(1)
式中,Ω为控制体,S为控制体边界,n为S微元的外法向单位矢量,其余各参数具体含义见参考文献[6]。采用有限体积法离散求解上述方程,黏性项采用二阶中心差分格式离散,流场分析基于全湍流假设,采用k-ωSST两方程湍流模型进行湍流数值模拟,时间推进采用双时间迭代方法。
1.2空间离散格式
本文中所采用的数值计算方法对无黏通量项离散选用基于迎风型通量差分分裂的Roe格式。针对Roe格式构造了基于改进的WENO方法对交界面两边状态参量进行重构的五阶Roe-WENO格式。
对于Roe格式,在三维贴体正交坐标系下,穿过网格单元界面的无黏通量可表示为
(2)
从(2)式可以看出,在采用Roe格式对N-S方程空间项进行离散求解时,首先要求得网格单元体交界面两侧变量的值qL和qR。通常对网格交界面左右两侧的变量是通过插值得到的。利用基于平均的网格中心点处的值来插值得到网格交界面处的变量值。因此,对交界面处变量插值的精度就决定了整个空间离散格式的精度。
由MUSCL插值方法得到的三阶迎风差分格式为
(3)
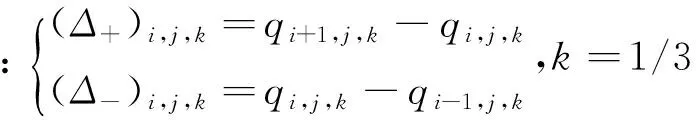
本文中采用改进的五阶WENO格式[7]对交界面两侧状态参量进行重构,以一维标量模型方程为例,五阶精度的边界外推值形式为
(4)
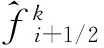
(5)
ωk为非线性加权因子,其定义如下
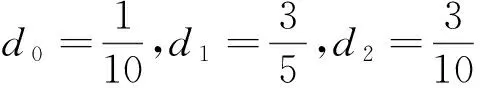
(6)
1.3动态面搭接网格技术通量传递
如何保证流场信息在搭接面准确传递,是动态面搭接技术的关键。对于图1给出的二维搭接面示意图,(i,j)表示Zone1中网格的格心,(l,m)表示Zone2中网格的格心。2块网格搭接面的网格点分别可表示为{xi+1/2,j;j=1,jmax}和{xl-1/2,m;m=1,mmax}。定义F为x方向上的通量,为了保证搭接面处的通量守恒,应有
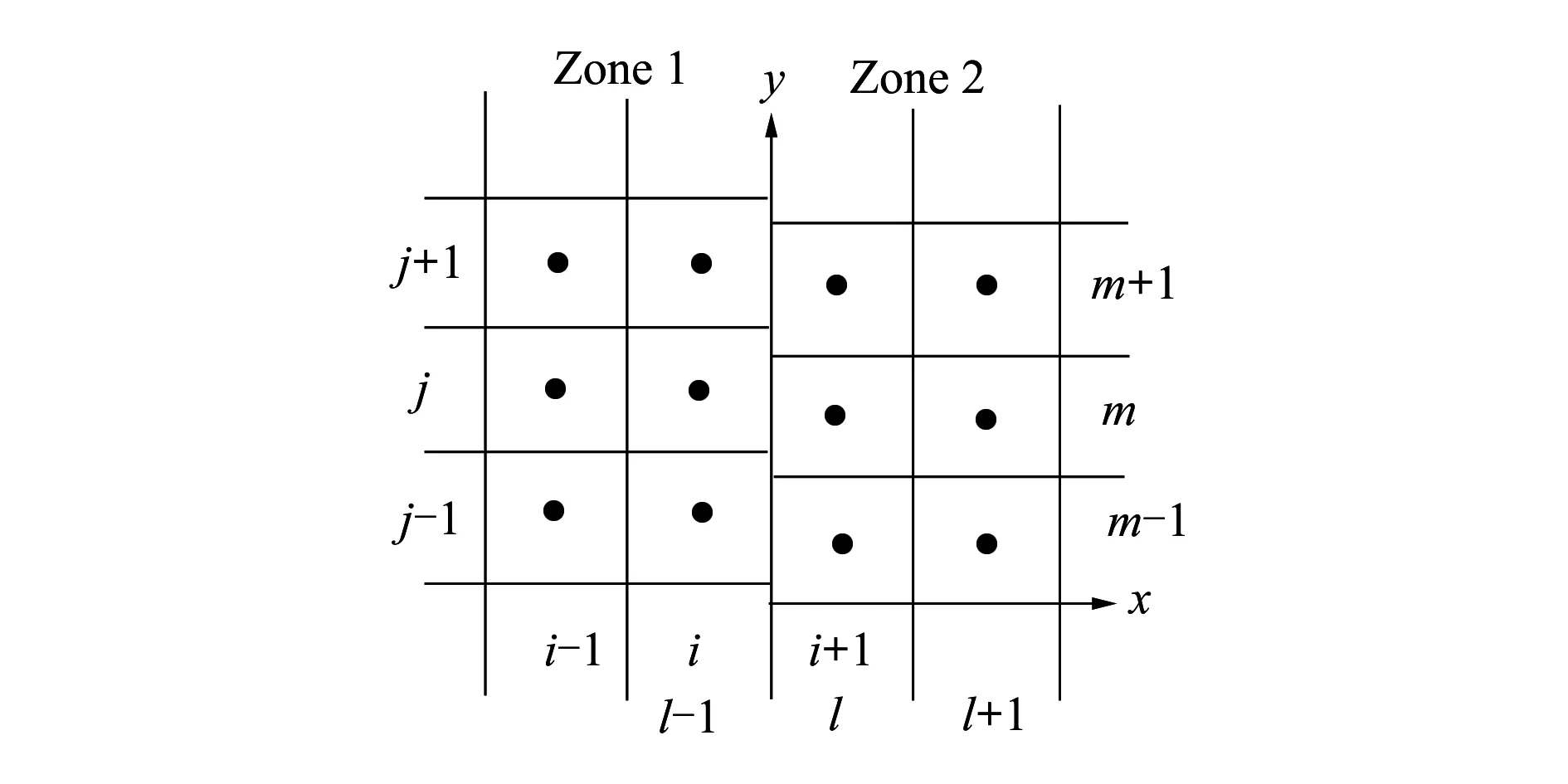
图1 二维搭接面示意图
(7)
(8)
(9)
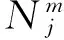
(10)
可以得到(7)式搭接面处通量守恒的离散形式
(11)
三维与二维情况最大的不同处在于,对于二维情况,2块网格的公共区域是一条线,而三维情况下公共区域是面。对于图2给出的三维搭接面示意图,Zone1的网格点用离散点集表示为
显然Zone1的搭接面为ξ=常数,可以写为
Zone2的搭接面也为ξ=常数,可以写为
在搭接面处的通量守恒方程为如下形式
(12)
相应的,(12)式的离散形式可以表示为
(13)
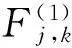
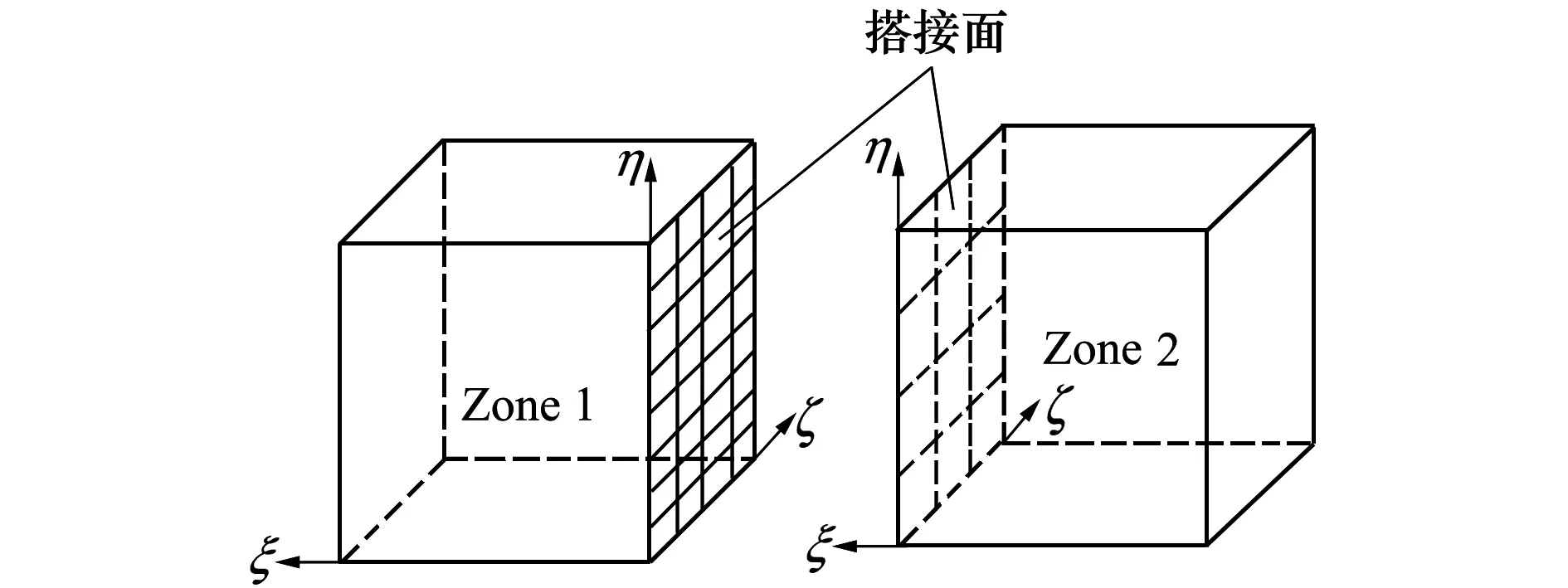
图2 三维搭接面示意图
2旋翼流场数值模拟
2.1Caradonna-Tung悬停流场数值模拟
Caradonna和Tung在1981年发表了一组旋翼压力测量的实验结果,该旋翼的实验装置及外形见参考文献[11],该旋翼包括2片桨叶,每片桨叶都是以NACA0012翼型为剖面的无扭转直机翼。桨盘半径R为1.143 m,展弦比为6。
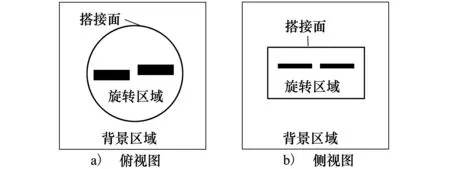
图3 网格分区示意图
采用ICEM CFD软件对整个计算域进行结构化网格划分,整个流场分为旋转区域及背景静止区域2个部分,2个区域通过搭接面传递信息,旋翼物面附近采用“O-O”型拓扑结构,其余地方采用“H-H”型拓扑结构,整个计算域网格节点总数为1 500万。图3给出了旋翼计算网格分区示意图,静止区域和旋转区域之间通过搭接面传递信息。选取的计算条件为:桨尖马赫数Mtip=0.44,桨叶桨距角θc=8′,基于桨尖弦长的雷诺数为Re=1.92×106。
图4给出了旋翼桨叶不同位置截面上的压力分布对比,虚线为三阶Roe-MUSCL格式的计算结果,实线为五阶Roe-WENO格式的计算结果。
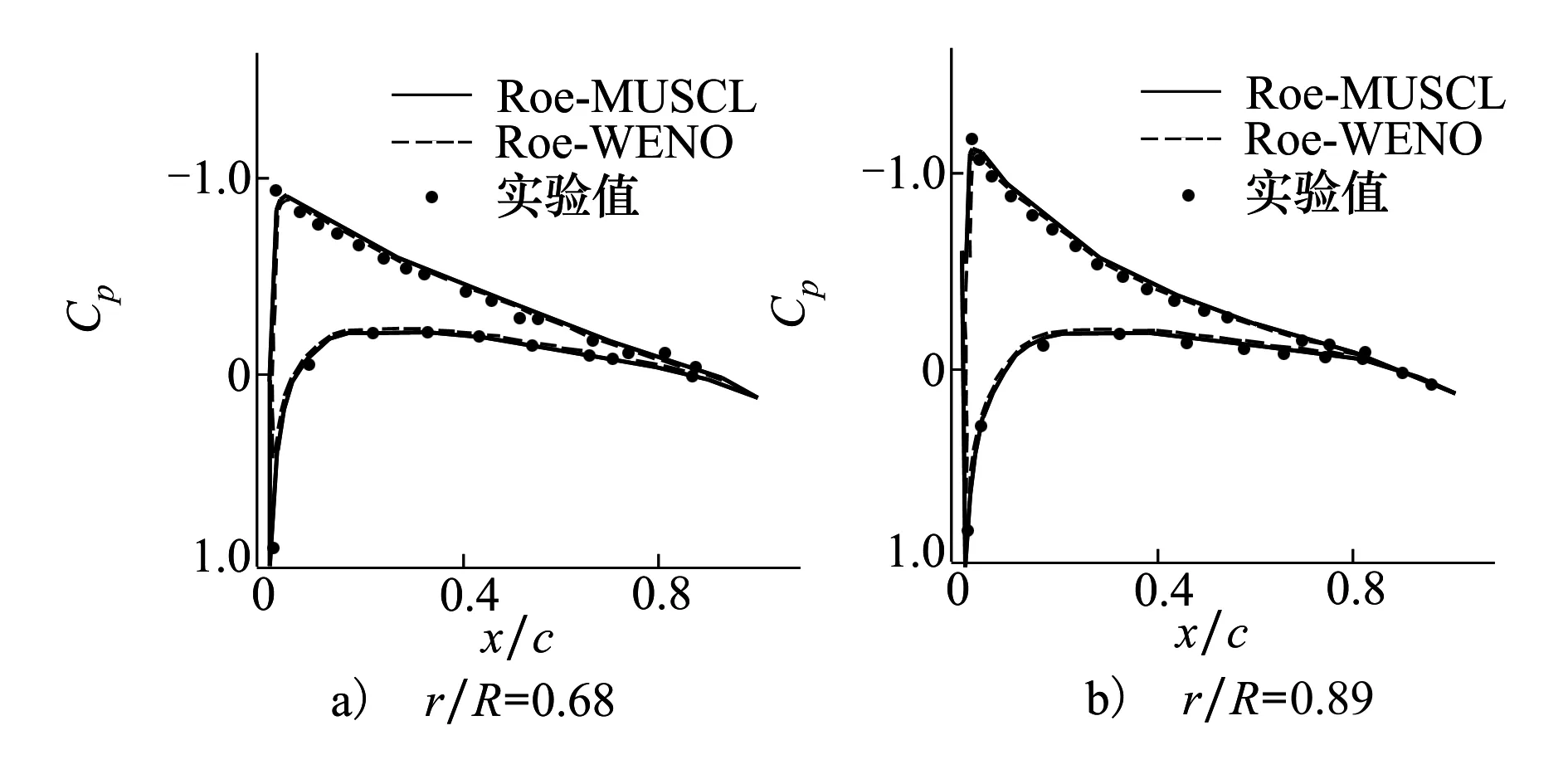
图4 桨叶表面压力分布
2种格式计算所得压力分布均与实验数据吻合得较好,仅桨叶上表面的压力分布略有差异,五阶Roe-WENO格式计算所得的前缘压力峰值与实验值更加接近,尤其是在靠近桨尖的附近区域。图5给出了涡量值为0.2时旋翼涡量等值面对比图。可以看到,在涡量值相同情况下,三阶Roe-MUSCL格式计算捕捉到的旋翼桨尖涡仅发展到了尾迹角240°左右,而五阶Roe-WENO格式计算捕捉到的旋翼桨尖涡发展到了尾迹角700°左右,从五阶Roe-WENO格式计算结果还能看到桨尖涡在向下发展的同时具有一定的收缩性,其涡核位置随着尾迹角增大向内收缩。
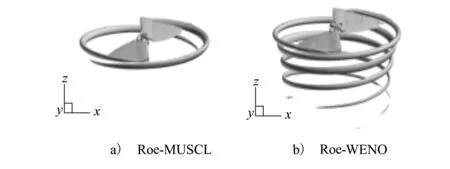
图5 涡量等值面对比图
图6给出了2种格式计算得到的旋翼空间截面上涡量等值线对比图。计算采用的Caradonna-Tung旋翼模型由2片桨叶构成,因此上下2个桨尖涡尾迹角相差180°。可以看到,Roe-MUSCL格式捕捉到的旋翼桨尖涡沿尾迹角发展了500°左右后就逐渐被耗散消失,而五阶Roe-WENO格式捕捉的旋翼桨尖涡沿尾迹角发展了900°后依然清晰可见。由于Roe-MUSCL格式的数值耗散较大,计算得到的桨尖涡外形有明显失真,从尾迹角180°开始上下相邻的桨尖涡粘连在一起,尾迹角360°后的桨尖涡形态基本难以辨认,同一尾迹角处的桨尖涡涡核位置与五阶Roe-WENO格式有明显差异。五阶Roe-WENO格式计算捕捉到的桨尖涡结构形态清楚,在同一尾迹角处的桨尖涡涡量明显强于Roe-MUSCL格式。
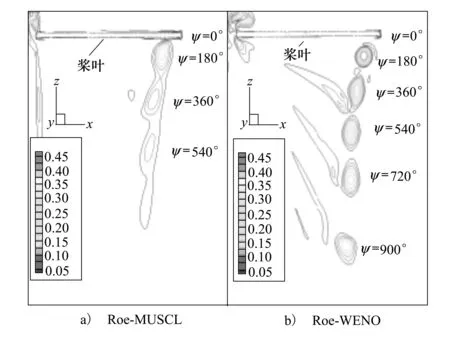
图6 空间截面涡量等值线对比图
从以上对比可以看出,本文所采用的五阶Roe-WENO格式数值耗散较低,对于旋翼桨尖涡的涡强度及发展过程预测要优于三阶Roe-MUSCL格式。
2.2Caradonna-Tung前飞流场数值模拟
本节主要检验本文所开发的计算程序对于旋翼前飞状态的数值模拟能力。计算采用的模型仍然为Caradonna-Tung旋翼,为了尽可能捕捉旋翼前飞过程中的桨尖涡,本文对尾迹区内的网格进行了加密,空间截面网格见图7,整个计算域网格节点数约为1 300万。

图7 网格示意图
空间离散采用五阶Roe-WENO格式,选取的计算状态为:桨尖马赫数Mtip=0.44,桨叶桨距角θc=8°,基于桨尖弦长的雷诺数为Re=3.66×106,前进比μ=0.3。该状态下旋翼做有升力前飞运动,桨叶前飞过程中无挥舞及变距现象。图8给出了旋翼桨叶展向r/R=0.89处不同桨叶方位角时的压力分布图,将本文计算结果与参考文献[5]的计算结果进行了对比,可以看到两者吻合得较好,再一次证明了本文采用数值方法的可靠性。
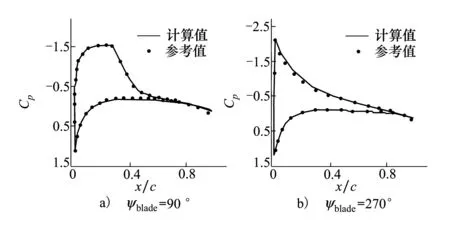
图8 压力分布对比图
图9给出了旋翼分别在桨叶方位角90°时的涡量等值面图,可以看到采用五阶Roe-WENO格式可以清晰捕捉到旋翼前飞过程中的尾涡结构。旋翼的桨尖涡在前飞过程中随着来流向后发展,分别在桨叶前行及后退一侧形成了一道集中涡束,在桨叶前行一侧,由于桨叶旋转速度与来流速度的叠加,桨尖涡强度较强,而在桨叶后退一侧,桨叶旋转速度与来流速度方向相反,桨叶当地的合成速度相对较小,导致向后发展的桨尖涡强度要弱。从图中还能观察到旋翼的桨-涡干扰现象,旋翼桨叶在前飞过程中都处于自身的尾涡干扰之中。
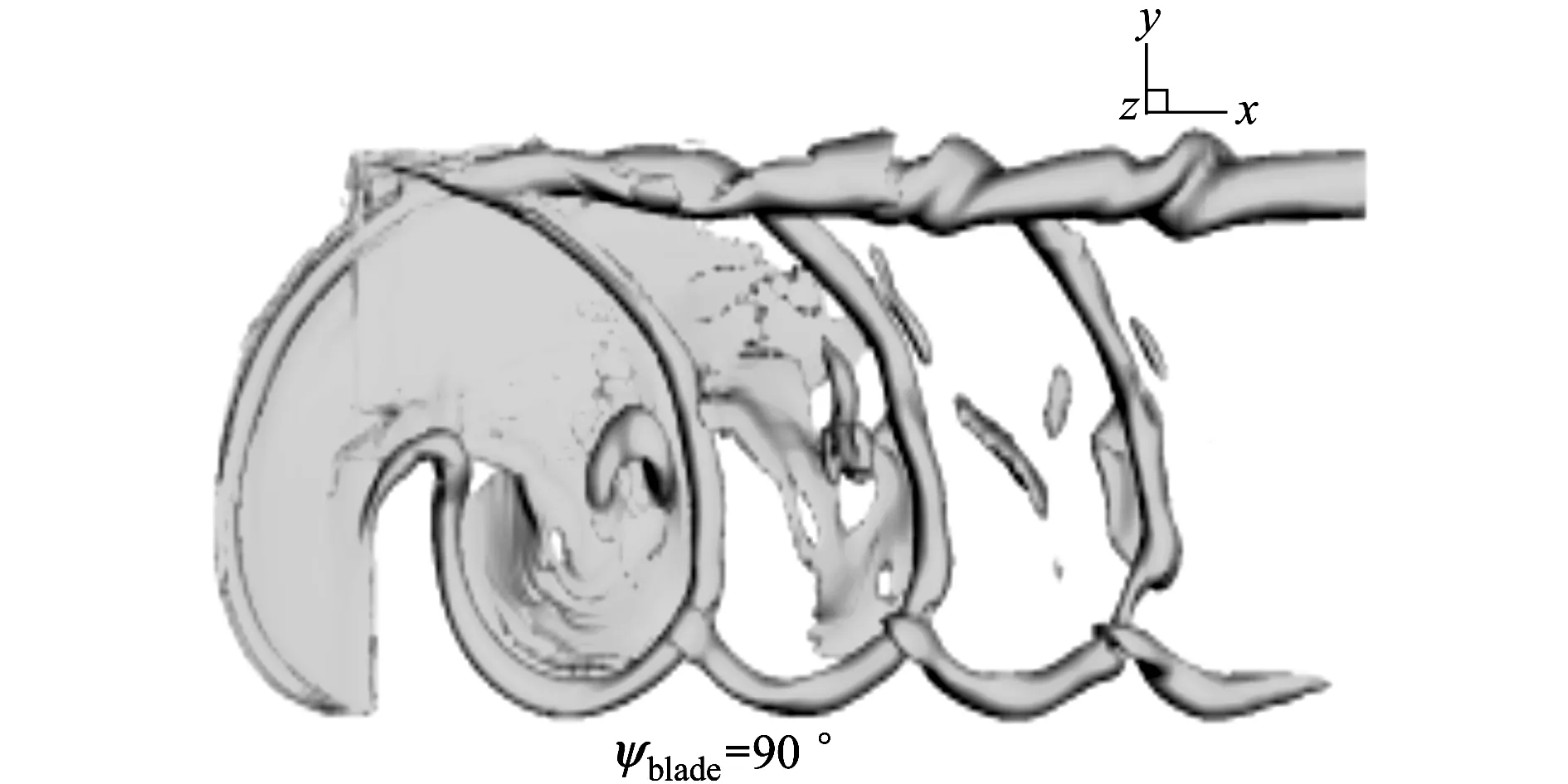
图9 涡量等值面图
3螺旋桨滑流机翼气动干扰问题
本节主要针对螺旋桨机翼组合构型进行非定常数值流动分析,进一步验证本文所采用的结构网格动态面搭接技术的可靠性。计算所采用的模型见图10,该模型与德宇航(DLR)Stuermer等研究的螺旋桨机翼组合模型AGARD2类似[4],不同的是Stuermer等采用的螺旋桨包含4片桨叶,本文采用的螺旋桨包含6片桨叶。所采用的机翼为平直机翼,采用的翼型为NACA0012对称翼型,机翼安装角为0°,机翼弦长为3 m,展长为12 m。
图10 螺旋桨机翼组合构型网格拓扑结构图
整个计算域网格节点总数约为900万。计算的状态为:来流迎角α=0°,来流马赫数Ma=0.15,螺旋桨转速为n=1 075 r/min,桨叶桨盘直径D=4 m。图11给出了螺旋桨机翼构型在有无螺旋桨情况下升力沿机翼展向的分布图,中心体两侧机翼的升力分布呈反对称分布,右侧由于螺旋桨桨叶向上旋转使得当地迎角增大从而产生正的升力,左侧则反之。图12给出了螺旋桨两侧对称的2个截面展向站位的压力分布对比。以上计算得到的结论与Stuermer等得到的结论一致,进一步验证了本文计算分析程序的可靠性。
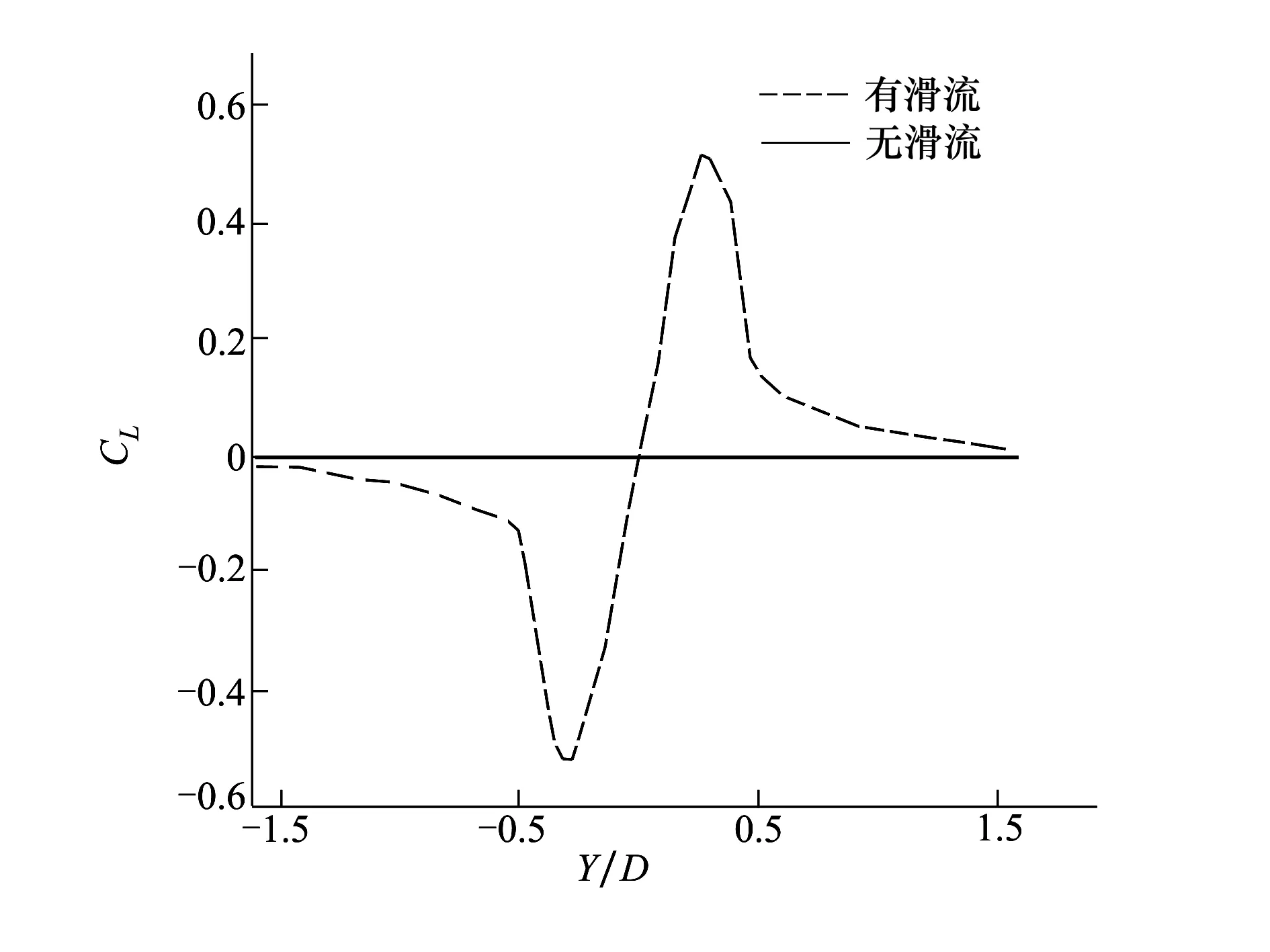
图11 有无滑流机翼展向升力系数对比
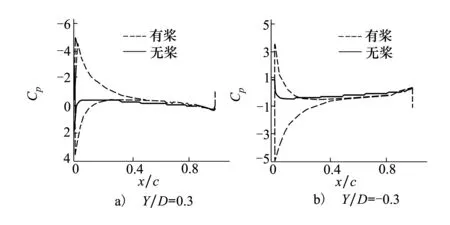
图12 有无螺旋桨滑流机翼表面压力分布对比图
4结论
针对旋转类问题非定常流动的数值模拟,本文基于结构网格动态面搭接技术、五阶Roe-WENO格式和非定常RANS方法开发了一套计算分析程序,并采用该计算程序对典型旋翼和螺旋桨算例进行了数值分析验证。分析结果表明:
1) 本文开发的计算程序具有较好的通用性,不仅可以用于旋翼悬停和简单前飞状态的数值模拟,对于螺旋桨及其他刚性旋转类问题也具有很好的适用性。
2) 所开发的计算程序具有较高的精度,在保证气动力分析可靠的同时,大大提高了旋转类问题的尾迹涡模拟精度,对于深入研究旋转类问题的流动机理具有重要的意义。
参考文献:
[1]王适存, 徐国华. 直升机旋翼空气动力学的发展[J]. 南京航空航天大学学报, 2001, 33(3):203-211
Wang Shicun, Xu Guohua. Progress of Helicopter Rotor Aerodymaics[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2001, 33(3): 203-211 (in Chinese)
[2]Srinivasan G R, McCroskey W J. Navier-Stokes Calculations of Hovering Rotor Flowfields[J]. Journal of Aircraft, 1988, 25(10): 865-874
[3]肖中云. 旋翼流场数值模拟方法研究[D]. 中国空气动力研究与发展中心, 2007
Xiao Zhongyun. Investigation of Computational Modeling Techniques for Rotor Flowfields[D]. China Aerodynamics Research and Development Center, 2007 (in Chinese)
[4]Stuermer A. Unsteady CFD Simulations of Propeller Installation Effects[R]. AIAA-2006-4969
[5]徐丽. 直升机旋翼非定常流动的低耗散高精度数值方法研究[D]. 上海: 上海大学, 2010
Xu Li. Numerical Research on High-Order Schemes with Low Dissipation for Unsteady Helicopter Rotor Flows[D]. Shanghai, Shanghai University, 2010 (in Chinese)
[6]周志宏.复杂流场NS方程及飞机结冰数值模拟[D]. 西安:西北工业大学,2011
Zhou Zhihong. Navier-Stokes Analysis in Complex Configurations and Icing Simulation on Airplanes[D]. Xi′an, Northwestern Polytechnical University, 2011 (in Chinese)
[7]Borges R, Carmona M, Costa B, et al. An Improved Weighted Essentially Non-Oscillatory Scheme for Hyperbolic Conservation Laws[J]. Journal of Computational Physics, 2008, 337: 3191-3211
[8]Lerat A, Wu Z N. Stable Conservative Multi-Domain Treatments for Implicit Euler Solvers[J]. Journal of Computational Physics, 1996, 123: 45-64
[9]Thomas James L. A Patched-Grid Algorithm for Complex Configurations Directed towards the F-18 Aircraft[R]. AIAA-1989-
0121
[10] Rai M M. A Relaxation Approach to Patched-Grid Calculations with Euler Equations[R]. AIAA-1985-0295
[11] Caradonna F X, Tung C. Experimental and Analytical Studies of a Model Helicopter Rotor in Hover[J]. Vertica, 1981, 5(2):149-161
收稿日期:2015-10-22基金项目:国家自然科学基金(11172240)、国家重点基础研究发展计划(2015CB755800)及航空科学基金(2014ZA53002)资助
作者简介:付炜嘉(1985—),西北工业大学博士研究生,主要从事飞行器设计空气动力学与计算流体力学的研究。
中图分类号:V211.3
文献标志码:A
文章编号:1000-2758(2016)03-0431-06
Unsteady Numerical Simulation of Rotor′s Flowfields Based on High-Order Scheme
Fu Weijia, Li Jie, Lou Qilin
(College of Aeronautics, Northwestern Polytechnical University, Xi′an 710072, China)
Abstract:A computational analysis procedure, which based on structure dynamic patched grid, the fifth-order Roe-WENO scheme and unsteady RANS method, was developed for the numerical simulation of the unsteady flowfiled of the rotor. Typical rotor examples were analyzed to verify the reliability of the procedure. Calculation results of the Caradonna-Tung rotor show that the calculated pressure distribution of the rotor is in good agreement with the experimental values. The developed procedure can be used for the numerical analysis of the aerodynamic performance of the rotor in hover or forward flight. In the case of the same computational grid distribution, the fifth-order Roe-WENO scheme has a higher resolution for the simulation of the rotor′s wake than that of the third-order Roe-MUSCL scheme and the wake of the tip vortex can be captured more clearly. The results of the propeller wing interference show that the developed procedure has good applicability for the unsteady simulation of the rigid rotation type of problem. The procedure developed by this paper has high accuracy of wake vortex simulation, it can meet the requirements of engineering applications.
Keywords:Structure dynamic patched grid, fifth order Roe-WENO scheme, rotors, propellers, unsteady flow

