基于BiSAR制导的战斗机最优引导律及导弹最优制导律设计

黄伟, 徐建城, 李俊兵, 吴华兴

(1.西北工业大学 电子信息学院, 陕西 西安　710072; 2.空军工程大学 航空航天工程学院, 陕西 西安　710038)



基于BiSAR制导的战斗机最优引导律及导弹最优制导律设计

黄伟1, 徐建城1, 李俊兵2, 吴华兴2

(1.西北工业大学 电子信息学院, 陕西 西安710072; 2.空军工程大学 航空航天工程学院, 陕西 西安710038)

摘要：针对半主动自寻的合成孔径雷达制导导弹发射后，战斗机、导弹的运动状态如何同时满足成像分辨率和脱靶量要求的问题，提出一种基于逆最优控制方法的战斗机引导律和导弹制导律。将成像分辨率对战斗机及导弹运动状态的双边约束，转化为对战斗机目标线角速度的单边约束；将脱靶量转化为对导弹目标线角速度的约束，从而实现导弹运动的自主性；建立含有待定权值系数的性能指标函数，根据所建立的战斗机引导系统和导弹制导系统的动态调节时间确定该系数，逆向得出最优引导律和最优制导律，仿真结果验证了该算法的有效性。

关键词：空对面导弹；双平台合成孔径雷达；传感器；目标；制导律；方位向分辨率；脱靶量；运动方程；约束优化；角速度；闭环控制系统；状态方程；反馈控制；控制器；动态响应

双平台合成孔径雷达(bistatic synthetic aperture radar,BiSAR)制导技术是先进成像制导技术极为重要的发展方向，相比单平台SAR制导模式，由于战斗机可配置大功率发射机，有效提高了导引头发现目标的距离，且导引头在作战使用过程中工作于静默状态，隐蔽性好、抗干扰和生存能力强[1]。

导引头的高分辨率成像是实现对目标精确打击的前提，在双平台同侧斜视的情况下，其距离向分辨率主要由发射信号的带宽决定，通过战斗机发射大带宽的线性调频信号以获得高的距离向分辨率，在技术上已不难实现。而方位向分辨率不仅与成像时间有关，还与制导平台相对目标的运动状态有关[2]。BiSAR双平台的运动状态如何在满足导引头方位向分辨率的同时，有效减小脱靶量，是BiSAR制导技术亟待解决的问题。目前，国内外对于SAR制导平台制导律的研究尚处于起步阶段，Fraooq、Jeremy等[3-4]对含有成像约束条件的空地SAR导弹的制导律问题进行了研究；谢华英、张刚、王杰等[5-7]应用遗传算法、SQP、Radau伪谱法对SAR制导平台的飞行轨迹进行了优化设计，以上研究成果所提出的制导律算法重点解决单基SAR的成像分辨率问题，性能指标函数中主要包含成像约束，未涉及脱靶量约束。文献[8]对BiSAR成像分辨率问题进行了研究，但双平台的运动仅限于特定轨迹。

BiSAR双平台的引导律及制导律设计可描述为多约束条件下的最优控制问题，其技术难点主要体现在：如何将成像分辨率对战斗机、导弹运动状态的双边约束，转化为对战斗机运动状态的单边约束，有效减小导弹脱靶量；如何使所建立的引导及制导系统具备给定的动态特性。基于此，本文通过分析BiSAR制导双平台运动状态与方位向分辨率之间的关系，将方位向分辨率和脱靶量约束分别转化为对战斗机和导弹运动状态的约束。基于逆最优控制，建立含有待定时变权值系数的性能指标函数，根据系统动态调节时间计算该系数，得出最优线性反馈控制器，使BiSAR双平台的运动状态同时满足成像分辨率和脱靶量要求。

1聚束式BiSAR方位向分辨率分析

典型的空地半主动SAR制导导弹发射后，战斗机连续照射目标成像区域，SAR导引头根据目标回波信号高分辨率成像。战斗机发射的线性调频信号归一化形式为

(1)

式中,Tp为脉冲时间宽度,τ=t-nTr为脉内时间,Tr为脉冲重复周期,n为脉冲数,fc为载波频率,γ为信号线性调频率,rect()为矩形函数。导引头接收的回波信号为[9]

(2)

式中,σn为目标散射系数,Ts为合成孔径时间,td=R(t)/c表示回波信号时延,设雷达波长为λ,回波信号经检波去除高频项可得[9]

(3)

式中,rect(t/Ts)e-j2πR(t)/λ项反映了战斗机、导弹相对目标运动的距离和史,决定了导引头的方位向分辨率。为便于分析,以战斗机发射导弹所在空间位置在地面上的投影点为原点建立地理坐标系OXYZ,战斗机和导弹构成非平行轨迹、收发平台不同速的一般双站构形[8],如图1所示。

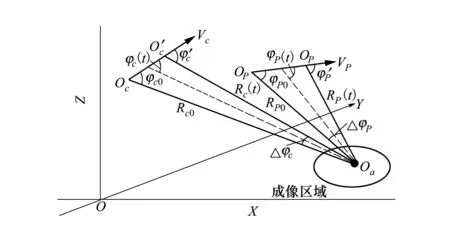
图1　战斗机、导弹与目标几何关系

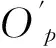
(4)

假设合成孔径时间内Vc和VP均为常值,由(4)式可得多普勒调频率为

(5)

(6)

方位向分辨率为[9]

(7)

(8)

(8)式建立了战斗机及导弹运动参数与导引头方位向分辨率之间的关系,假设导引头所需方位向分辨率为ρaT,将(8)式中的ρa设定为常值ρac(ρac≤ρaT),并假设已知ωp、Vp和Vc,方位向分辨率要求可转化为对战斗机运动状态的约束

(9)

式中,ωcT是战斗机为满足导引头方位向分辨率要求所对应的理想目标线角速度。

2最优引导律及制导律设计

考虑到双平台运动状态的复杂性,为简化问题,假设制导过程中战斗机、导弹和目标均位于空间不变的方位向平面内,根据三者之间相对运动关系的数学模型以及制导过程的各项指标要求,将BiSAR制导问题转化为最优控制问题,以战斗机及导弹的目标线法向加速度为控制量,建立含有待定系数的性能指标函数,根据系统的动态调节时间计算该系数,逆向得出最优控制量(战斗机最优引导律和导弹最优制导律),从而保证成像分辨率和有效减小脱靶量。

2.1战斗机、导弹与目标的相对运动关系建模

空地半主动SAR制导导弹主要用于攻击地面固定或慢速移动的目标,由此可忽略目标运动的影响,并假设战斗机和导弹均为质点,在方位向平面内,战斗机、导弹与目标的相对运动关系如图2所示。

图2　战斗机、导弹相对目标运动关系

图2中,以战斗机发射导弹所在的空间位置为原点建立方位向平面坐标系OXY。当前时刻,战斗机位于Oc点,导弹位于Op点,Oa为地面目标点,θc与εc分别为战斗机偏航角及目标线角,θp与εp分别为导弹偏航角及目标线角。将战斗机速度矢量Vc投影到目标线OcOa及其法线上,可得

(10)

(11)

(12)

上式即为战斗机与导弹相对目标的运动学方程,jc和jp分别为战斗机及导弹在方位向平面的目标线法向加速度。

2.2引导律和制导律算法的建立

假设方位向平面内所有量测都准确、理想,控制量仅为战斗机和导弹在方位向平面的目标线法向加速度。根据(12)式可得状态方程标准形式

(13)

式中

建立性能指标函数基于如下考虑:①为满足导引头方位向分辨率要求,制导过程中战斗机实际目标线角速度ωc应趋近于(9)式表示的理想目标线角速度ωcT;②为有效减小导弹脱靶量,导弹实际目标线角速度ωp应趋于零[10];③控制过程的经济性。由此,建立二次型性能指标函数

(14)

式中

Q(t)和R(t)均为待定权值系数矩阵。不难证明,(13)式所表示的系统状态方程是能控的,根据最优控制理论,可得最优控制量为

(15)

P(t)满足黎卡提方程及边值条件

(16)

考虑到结束控制时刻tk难以准确估计以及黎卡提方程求解的复杂性,有关学者在进行大量的装备验证之后,在文献[11]中指出:由于导弹与目标运动状态的剧烈变化,制导过程的每一时刻t都可能对应结束时刻tk,即t→tk,在引导律或制导律设计过程中,可直接应用P(t)的稳态解[11]

(17)

由(9)式、(13)～ (17)式可得含有待定系数的最优控制量分别为

(18)

(19)

2.3待定系数的计算

2.3.1系数q22/k22的计算

设Rp0和Rpk分别为弹目初始距离和结束控制时刻距离,令λ1=q22/k22。假设导弹自动驾驶仪无迟滞的响应jp,将(19)式代入(13)式,可得导弹闭环制导系统状态方程为

(20)

(21)

由上式进一步推导可得

(22)

(23)

(24)

由于制导初始距离Rp0远大于结束距离Rpk,实际应用过程中(24)式可简化为经典的比例导引算法式jp=NpVpmωp,根据作战使用的具体要求可调整比例系数Np,并满足jp≤jpmax的限制条件,jpmax为导弹最大目标线法向加速度。

2.3.2系数q11/k11的计算

(25)

(25)式所表示的一阶微分方程的解为

(26)

对(26)式进一步推导可得

(27)

(28)

(29)

(30)

比例系数Nc的取值应着重考虑作战使用的具体要求并满足jc≤jcmax的限制条件,jcmax为战斗机最大目标线法向加速度。

通过上述分析知,本文所建立的控制算法是成像分辨率、制导准确性、控制经济性及动态性能综合最优的。应该注意到,比例系数Np和Nc的取值不仅影响控制量系数,而且影响性能指标函数的权值系数,其原因在于所建立的性能指标函数本身含有待定系数,根据条件确定待定系数后,控制量和性能指标函数随之确定。也就是说,根据作战使用的具体要求调整比例系数不会影响所得到控制量的最优性,从而体现出该控制算法的适用性。

3仿真实例

仿真过程中,假设战斗机、导弹和目标均为质点,战斗机和导弹飞行控制系统无迟滞的响应(24)式和(30)式给出的指令加速度,由于战斗机比例系数Nc的取值决定战斗机趋近于理想运动状态的快慢程度,与导弹运动状态无关,所以为说明Nc对方位向分辨率的影响,选取Nc=4和Nc=15进行对比仿真验证。

在图2所示的方位向平面坐标系中,战斗机与导弹的初始位置坐标均为(0,0),初始速度分量均为Vx=0.2 km/s、Vy=0.6 km/s,地面目标点位置坐标为(40km,40km),其他参数如表1所示。

表1　仿真参数

仿真实例1:战斗机比例系数Nc=4(简称N4)。仿真结果如图3所示。

图3　N4控制算法仿真结果

图3a)给出了当Nc=4时,战斗机与导弹在方位向平面的运动轨迹,仿真初始时刻战斗机位于坐标原点并发射导弹,制导过程中战斗机为满足导引头成像分辨率要求,运动轨迹较导弹弯曲。图3b)对应制导过程中战斗机与导弹的目标线法向过载,由图可知,战斗机和导弹的过载均在容许范围内,导弹过载随制导时间不断减小,这将有利于制导过程中成像平台的稳定。

图3c)给出了战斗机与导弹的目标线角速度变化情况。由图可知,导弹目标线角速度不断减小,而战斗机目标线角速度不断增大,制导结束时刻ωp=0.001rad/s,经计算可得理想脱靶量为h=0.21m,满足导弹脱靶量要求。图3d)给出了实际方位向分辨率ρa的变化情况,ρa随制导时间不断增大,在制导末段ρa>ρaT,说明当Nc=4时战斗机的引导律不满足导引头的分辨率要求。

仿真实例2:战斗机比例引导系数Nc=15(简称N15)。仿真结果如图4所示。

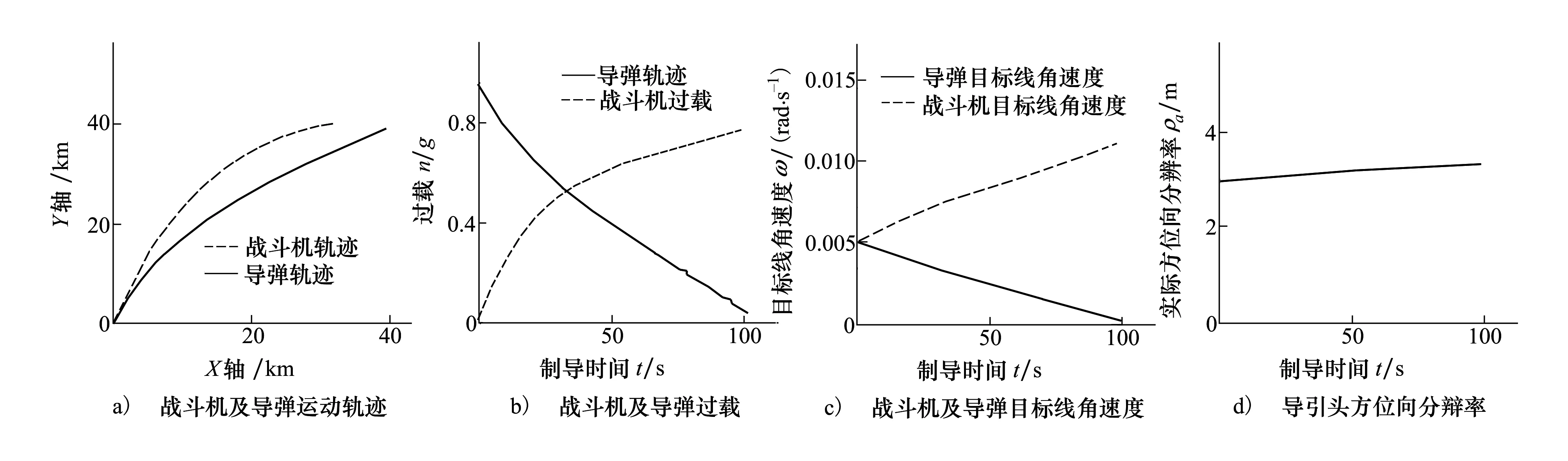
图4　N15控制算法仿真结果

图4a)和图4b)分别给出了当Nc=15时,战斗机与导弹的运动轨迹及过载变化情况,对比N4的仿真结果,战斗机N15轨迹相比N4弯曲,过载量也较大,N15结束制导时刻战斗机与目标的距离相对较小。图4c)和图4d)分别给出了战斗机与导弹的目标线角速度和实际方位向分辨率ρa的变化情况。由图4d)可知,整个制导过程中ρa<ρaT,满足导引头方位向分辨率要求。

分析N4和N15情况下的仿真结果可知,由于加大了战斗机的引导比例系数,使实际方位向分辨率ρa趋近于设定值ρac,由于ρac的取值比导引头所需分辨率ρaT小,从而保证了制导过程中ρa<ρaT。但应注意到,增大系数Nc将导致末制导阶段战斗机与目标距离相对较小,战斗机极易遭受敌防空火力的打击,作战过程中应根据导引头所需分辨率和实际作战环境确定Nc的取值。

4结论

本文提出的算法有效解决了对于空地BiSAR制导平台而言，较为特殊的轨迹控制问题，研究总结如下：①算法综合考虑了制导过程中成像分辨率和脱靶量要求，经仿真验证，满足各项指标要求；②导弹制导律算法的建立仅基于脱靶量要求，与成像分辨率及战斗机运动状态无关，体现了导弹运动状态的自主性，提高了攻击目标的准确性；③战斗机引导律比例系数可根据导引头成像分辨率要求及实际战场环境调整，体现了该算法的适用性。

为实现该算法，战斗机和导弹在硬件上应具备数据链功能，导弹实时将运动参数回传至战斗机。如果攻击大型目标，对目标方位向分辨率要求较低时，可预先估计导弹的运动参数，此时战斗机可以按照预先规划的航线飞行。

参考文献：

[1]邓宝. 对SAR的干扰压制区计算模型[J]. 系统工程理论与实践, 2008,28(1):151-155

DengBao.TheSuppressingAreaComputingModelofJammingSAR[J].SystemsEngineering-Theory&Practice, 2008, 28(1): 151-155 (inChinese)

[2]史洪印,周荫清,陈杰. 平飞模式机载双基地SAR动目标检测方法[J]. 北京航空航天大学学报,2009,35(8):996-1000

ShiHongyin,ZhouYinqing,ChenJie.GroundMovingTargetDetectionMethodofParallelModeAirborneBistaticSAR[J].JournalofBeijingUniversityofAeronauticsandAstronautics, 2009, 35(8): 996-1000 (inChinese)

[3]FarooqA,LimebeerDJN.OptimalTrajectoryRegulationforRadarImagingGuidance[J].JournalofGuidance,ControlandDynamics, 2008, 31(4): 1076-1092

[4]HodgsonJA,LeeDW.TerminalGuidanceUsingaDopplerBeamSharpeningRadar[C]∥AIAAGuidance,NavigationandControlConferenceandExhibit,Austin,Texas,America, 2003: 1-11

[5]谢华英,范红旗,赵宏钟,等.SAR成像导引头的弹道设计与优化[J]. 系统工程与电子技术,2010,32(2):332-337

XieHuaying,FanHongqi,ZhaoHongzhong,etal.TrajectoryDesignandOptimizationforaSARSeeker[J].SystemsEngineeringandElectronics, 2010, 32(2): 332-337 (inChinese)

[6]张刚,祝明波,陈瑜,等. 基于SQP算法的SAR成像导引头三维弹道优化[J]. 计算机工程与科学,2012,34(4):146-150

ZhangGang,ZhuMingbo,ChenYu,etal. 3DTrajectoryOptimizationoftheSARImagingSeekerBasedanSQP[J].ComputerEngineering&Science, 2012, 34(4): 146-150 (inChinese)

[7]王杰,张刚,杨立波,等. 基于Radau伪谱法的SAR末制导成像段弹道优化[J]. 现代防御技术,2013,41(5):41-45

WangJie,ZhangGang,YangLibo,etal.TrajectoryOptimizationofSARImagingGuidanceBasedanRadauPseudospectralMethod[J].ModernDefenseTechnology, 2013, 41(5): 41-45 (inChinese)

[8]易予生,张林让,刘昕,等. 机载双站合成孔径雷达模糊函数分析[J]. 系统工程与电子技术,2009,31(11): 2598-2601

YiYusheng,ZhangLinrang,LiuXin,etal.AnalysisoftheAmbiguityFunctionforAirborneBistaticSARSystem[J].SystemsEngineeringandElectronics, 2009, 31(11): 2598-2601 (inChinese)

[9]杨汝良. 高分辨率微波成像[M]. 北京:国防工业出版社,2013: 18-81

YangRuliang.HighResolutionMicrowareImaging[M].Beijing,NationalDefenseIndustryPress, 2013: 18-81 (inChinese)

[10] 郭建国,周军. 基于Nussbaum-Type增益技术的末制导律设计[J].西北工业大学学报,2010,28(5):753-757

GuoJiangguo,ZhouJun.DesigningaNewandBetterTerminalGuidanceLawBasedonNussbaum-TypeGainTechnique[J].JournalofNorthwesternPolytechnicalUniversity, 2010,28(5): 753-757 (inChinese)

[11]KhannaSK,MailerK.AeronauticalRadioControlSystem[M].Moscow:RadioTechnologyPress, 2003: 65-81

收稿日期：2015-10-27

基金项目：国家自然科学基金 (61472441)资助

作者简介：黄伟(1980—)，西北工业大学博士研究生，主要从事SAR成像制导技术的研究。

中图分类号：V249；TJ765.3

文献标志码：A

文章编号:1000-2758(2016)03-0367-07

Design of Optimal Guidance Laws of Fighter and Missile Based on BiSAR Guidance

Huang Wei1, Xu Jiancheng1, Li Junbing2, Wu Huaxing2

1．School of Electronics Information，Northwestern Polytechnic University，Xi'an 710072，China2．Aeronautics and Astronautics Engineering College，Air Force Engineering University，Xi'an 710038，China

Abstract:To meet the requirements of resolution at the azimuth and miss distance for motion states of Bi-SAR platforms which indicates the fighter aircraft and the semi-active homing SAR-guided missile after launch, guidance laws for the aircraft and missile based on inverse control algorithm are proposed. Two-sided constraints due to resolution for their motion states is converted to one-sided constraint for the aircraft's angular velocity of line of sight, and miss distance is considered as only constraint for the missile's angular velocity of line of sight to implement its autonomy of motion. Performance index function containing undetermined coefficients is build and the coefficients are calculated according to dynamic tuning time for both guiding systems, and their optimal guidance laws are derived inversely. Simulation results demonstrate the validity of the algorithm.

Keywords:air to surface missiles; bistatic synthetic aperture radar; sensors; targets; guidance law; resolution at the azimuth; miss distance; equations of motion; constrained optimization; angular velocity; closed loop control systems; equations of state; feedback control; controllers; dynamic response