一种有效的组合导航容错滤波技术研究
耿 峰, 祝小平,周 洲
1. 西安导航技术研究所,陕西西安710068; 2. 西北工业大学第365 研究所,陕西西安7100723. 西北工业大学航空学院,陕西西安710072
一种有效的组合导航容错滤波技术研究
耿 峰1,2, 祝小平2,周 洲3
1. 西安导航技术研究所,陕西西安710068; 2. 西北工业大学第365 研究所,陕西西安7100723. 西北工业大学航空学院,陕西西安710072
摘要:为解决INS/多天线GNSS/MHS/DNS组合导航系统,一个或多个传感器的导航信息出现错误,导致整个组合导航系统定位精度严重下降甚至无法定位的问题,提出一种多模式联邦高斯和粒子容错滤波技术,提高组合导航系统的鲁棒性。该滤波技术基于无重置联邦滤波结构,考虑到组合系统的非线性非高斯特性,局部滤波采用高斯和粒子滤波算法,以提高滤波精度,同时利用粒子似然函数方法,进行局部滤波器故障检测并隔离,进而,根据检测与隔离结果,进行全局滤波模式切换与全局最优估计,最终得到精确可靠的导航信息。仿真分析结果表明,多模式联邦高斯和粒子容错滤波技术是有效的,在多个子系统出现故障情况下,组合导航系统仍能提供精确的导航信息。
关键词:导航;组合;容错;故障诊断;传感器
当前,越来越多的导航传感器应用到了航空、航天、船舶等领域中,这也使得基于多传感器的组合导航系统愈加完善。不过伴随而来的是,组合导航系统的复杂性也随之大为增加,这对系统的可靠性带来了巨大考验,特别是面对航空、航天、领域传感器所处的恶劣工作环境。实际应用中,个别传感器或子系统难免发生故障,而传感器或子系统的故障往往会将错误的信号或测量信息带入整个组合导航系统,从而导致系统的信息可靠性和精度大幅下降,严重情况下甚至会导致整个系统提供的信息失效、不可用。因此,非常有必要开展组合导航容错系统相关技术研究,以保证系统测量精度的同时提高其可靠性。
组合导航系统多采用冗余的传感器配置方案(诸如陀螺、加速度计)以及采用多种辅助导航系统(如GNSS、CNS、DNS、GNS、BPNS等),为容错设计提供了硬件基础。在组合导航系统信息融合研究方面,目前主要有集中式滤波、分散滤波、级联式滤波以及联邦滤波等4种比较成熟的融合技术,其中,联邦滤波技术[1-2]克服了集中滤波技术计算量大、容错性能差的不足,具有算法复杂程度低,容错性和可靠性好,设计简单灵活,便于工程实现等突出特点。
组合导航系统的故障检测与隔离(FDI)技术是一项专门技术。目前,针对基于联邦卡尔曼滤波的组合导航系统,常用的故障检测方法有状态χ2检测法和残差χ2检测法[3]。状态χ2检测法利用2个状态估计的差异对组合系统的故障进行检验。该检测法对于软故障和硬故障都有较好的检测效果,但计算量比较大。残差χ2检测法利用信息序列作为估计量对组合系统进行故障检测。该检测法具有计算量较小的优点。但对于软故障,检测效果不是很理想。
近年来,非线性非高斯系统的故障诊断问题也成为热点问题。对非线性非高斯系统的故障检测相对比较困难,目前,还没有最优的解决方法。梁军等研究了基于SIR粒子滤波状态估计和残差平滑的故障检测算法对于非线性非高斯系统的故障检测取得了较好的效果[4]。葛哲学等提出了序贯式故障诊断策略,采用负对数似然比方法监控系统的运行状态,故障发生后利用状态联合估计器进行故障隔离。该方法能实时检测诊断出非线性系统的故障,同时能抑制非高斯噪声的影响[5]。
为了提高INS/多天线GNSS/MHS/DNS组合导航系统的容错能力,本文提出了一种多模式联邦高斯和粒子容错滤波技术。该技术基于联邦滤波架构,在局部滤波器设计中,针对组合导航系统测量动态模型具有非线性和非高斯的特点,采用高斯和粒子滤波算法。与其他传统的滤波算法比较,高斯和粒子滤波能够很好地解决非线性滤波问题,并且不需要要求测量噪声必须服从高斯分布这样的制约条件。针对非线性非高斯系统的故障检测问题,采用基于粒子似然函数的故障检测方法。另外,针对故障传感器的不同,专门设计不同的传感器组合滤波模式,根据故障检测和隔离结果,选择适合的滤波模式,将重构的局部滤波结果,进行全局滤波,最终得到全局最优估计。
1多模式联邦容错滤波结构
多模式联邦容错滤波器由一个公共参考传感器和若干个子传感器构成,每个子传感器的输出与公共参考传感器的输出一起作为子滤波器(局部滤波器)的量测量,而每个子滤波器的滤波运算是平行的和不相关的,通过子滤波器,可获得系统状态的局部最优估计,如果各子滤波器没有发生故障,那么,这些局部最优估计随后在主滤波器中进行融合得到最优全局估计,如果个别子滤波器发生故障,则采用相应的故障检测方法,进行故障检测与隔离,并触发对应的滤波模式切换逻辑,进行模式切换,重构局部滤波结果,然后,送入主滤波器进行全局滤波,最终到容错后的全局最优估计。多模式联邦容错滤波器结构如图1所示:

图1 多模式联邦容错滤波器结构
采用惯性传感器网络单元(ISNU)作为公共参考传感器。ISNU是一种基于集束传感器技术的冗余IMU系统,其能够最有效地利用由多传感器提供的冗余测量信息,具有很高的可靠性。例如,一种由3个单自由度加速度计和3个单自由度陀螺仪组成,其几何结构为正十二面体结构的惯性传感器网络单元平均无故障时间为0.95λ-1(假设每个加速度计和陀螺仪的故障率均相同且大小恒定不变),与通常的含3个正交配置陀螺仪的IMU平均无故障时间的比值为2.86,可以看出该惯性传感器网络的可靠性大幅提高。
由于组合导航系统中存在一定的非线性环节,比如在 GNSS/惯性组合模式中,伪距观测方程为非线性的,此外,测量噪声还服从非高斯分布,是一典型的非线性非高斯系统,因此,传统的联邦卡尔曼滤波技术无法取得令人满意的滤波精度。针对这一非线性非高斯系统,本文在联邦滤波器局部滤波中,采用基于高斯和的粒子滤波技术,并且采用粒子似然函数方法进行传感器子系统故障检测。
2多模式联邦高斯和粒子容错滤波算法
2.1正规化滤波器测量方程[6]
2.1.1正规化位置和速度偏差方程
如果可得到多天线GNSS(MA-GNSS)接收机提供的导航状态量,数据融合滤波器的正规化测量方程如下:
1) 位置偏差方程
(1)
2) 速度偏差方程
(2)
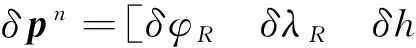
多普勒导航系统(DNS)是一种机载自治航位推算系统。多普勒雷达(DR)安装在载体的正下方,通过测量从地面返回的雷达波束信号的多普勒频移,能够获得载体相对于地面的速度矢量。多普勒导航方程如下
(3)
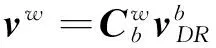
INS和多普勒雷达得到的速度之间的偏差方程正规化形式如下
(4)
2.1.2正规化姿态偏差方程
当MA-GNSS接收机和其它传感器系统能够提供载体的姿态信息时,姿态偏差方程的正规化形式如下
(5)
式中,θAided为由MA-GNSS或其它姿态测量系统提供的欧拉角,θINS为由INS提供的欧拉角,νAtt为姿态测量噪声。Ttilt-θ为倾斜角到欧拉角的转换矩阵,表示如下
(6)
对于磁航向传感器(magneticheadingsensor,MHS)来说,其相应的测量方程如下
(7)
式中,bM为磁航向偏差量,νM为测量噪声。bM可由一个随机常量外加一阶马尔科夫过程表征。
2.2时间统一
确定分段时间间隔Ts。为避免分段时间间隔内无测量数据的情况出现,Ts不小于相应传感器的最大采样周期,故取Ts=Tmax。
划分重叠区间TΔ,如下
(8)

(9)
二次型误差函数为
(10)
求导得
(11)
(12)

2.3子滤波器滤波算法
组合导航系统的动态状态空间模型(DSS)为非线性非高斯系统,其中,非线性主要体现观测方程的非线性上,非高斯则主要是模型测量噪声服从非高斯分布。为了取得满意的滤波精度,在局部滤波中,采用高斯和粒子滤波算法。
高斯和粒子滤波算法[7-9]是一种非线性滤波算法,利用有限高斯密度的加权求和来近似非高斯概率密度,并利用粒子滤波中的粒子及其权值,最终求得各高斯密度的均值和方差的估计值。
动态状态空间模型描述如下
(13)
式中,un和νn为非高斯噪声。到时刻n的信号和观测量分别被记作x0:n和y0:n,x0:n={0,…,xn},y0:n={0,…,yn}。
2.3.1时间更新
假设n-1时刻,有先验概率密度函数为
(14)


(15)
而条件转移密度的高斯和分布形式如下
(16)
则,预测分布(预测密度函数)可描述为
(17)
由
(18)
可得到时间更新的预测密度函数为
(19)
定义i=j+(k-1)K,那么,j=1,…,G,k=1,…,K,i=1,…,GK。时间更新算法如下:

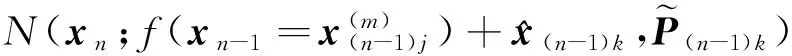

(20)
(21)
④对于j=1,…,G,k=1,…,K以及i=1,…,GK,其中,i=j+(k-1)K,根据下式更新权重。
(22)
2.3.2测量更新
假设n时刻,有预测分布
(23)
则,滤波分布可表示为
(24)
测量更新算法如下:

②对于j=1,…,M,i=1,…,GK,计算权重
(25)
③对于i=1,…,GK,估计每个高斯分布的均值和协方差
(26)
(27)
④对于i=1,…,GK,更新每个高斯分布的权重,并归一化
(28)

2.4主滤波器滤波算法
主滤波器将各个子滤波器的局部估计值信息进行融合,得到全局的最优估计值和最优估计方差阵。
(29)
2.5故障检测与隔离
针对子滤波器非线性动态特性,故障检测采用基于粒子似然函数的故障检测方法。即就是,当传感器工作正常时,各粒子的似然函数均值较高,而当发生故障时,各粒子的似然函数均值较小,将粒子的似然函数平均值的对数和当作表征故障的残差值,当该残差值大于预设阈值时,则认为传感器发生故障,反之,认为传感器无故障。具体过程如下:

②求全部粒子的似然函数平均值Lni;
(30)
③求最近K个时刻内Lni的对数和dni;
(31)
④如果dni小于阈值,则判断未发生故障,否则判断发生故障。
若判断出所有子系统无故障,则把滤波值送至主滤波器;若某个子系统故障,则对其隔离。
2.6多模式切换与系统重构
通过故障检测与隔离,若某个子系统出现故障,则立即对其进行隔离,同时启动模式切换逻辑,选择对应的组合滤波模式,对系统进行重构,将重构后的局部滤波估计结果送入主滤波器进而得到最终的全局最优估计结果。切换模式如表1所示。

表1 可供切换的模式
3仿真验证与分析
仿真时间取2 400s,子滤波器粒子滤波采样样本数为6 000,载体运行轨迹如图2所示,由平飞、爬升和转弯等状态组成。载体初始位置为东经118°、北纬 32°、高度1 000m,初始速度为280m/s。
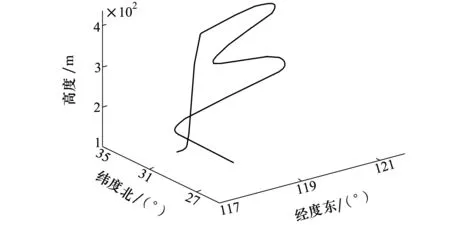
图2 载体运行轨迹
INS/MA-GNSS/MHS/DNS组合导航系统仿真参数设置如表2所示。ISNU输出频率为50Hz,MA-GNSS接收机输出频率为5Hz、MHS和DR输出频率均为1Hz。

表2 组合导航系统仿真参数设置
上述所有误差参数的动力学模型为由随机常数过程、随机游动过程以及一阶非高斯马尔可夫随机过程组成的联合随机过程。
在仿真中,设置2种类型的故障分别为突变故障(硬故障)和慢变故障(软故障)。突变故障设置为阶跃型常值偏置,慢变故障设置为斜坡信号或抛物线信号,各子系统的故障设置如表3所示。

表3 各子系统的故障设置
主滤波器滤波结果如图3~图5所示。各子系统无故障、各子系统发生故障(见表3)但不进行故障检测隔离以及各子系统发生故障并进行故障检测隔离与重构等3种情况下,全局滤波误差统计结果见表4。

表4 全局滤波误差统计结果
从仿真结果可以看出,各子系统无故障时,全局滤波具有较高的精度,证明对于非线性非高斯系统,高斯和粒子滤波算法拥有很好的滤波性能;当各子系统发生如表3所示故障时,不进行故障的检测与隔离,全局滤波精度大幅下降,而引入粒子滤波似然函数故障检测方法进行故障检测、隔离以及重构后,主滤波器滤波精度与子系统无故障时的滤波精度相当,证明粒子滤波似然函数故障检测方法是有效的。
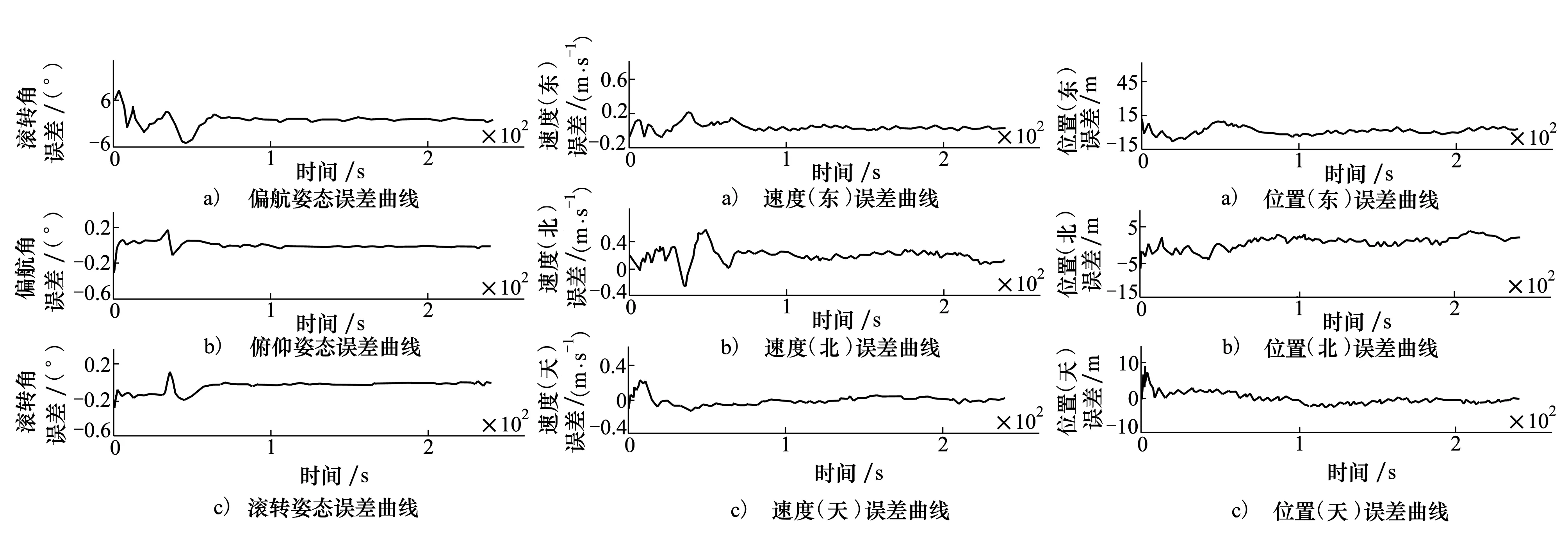
图3 主滤波器全局最优估计(姿态误差) 图4 主滤波器全局最优估计(速度误差) 图5 主滤波器全局最优估计(位置误差)
4结论
针对INS/多天线GNSS/MHS/DNS组合导航系统中,一个或多个传感器导航信息出现错误,导致整个组合导航系统定位精度严重下降甚至无法定位的问题,本文提出了一种多模式联邦高斯和粒子容错滤波技术。针对组合导航系统测量动态模型具有非线性和非高斯的特点,局部滤波采用了高斯和粒子滤波算法。与其他传统的滤波算法比较,高斯和粒子滤波能够很好地解决非线性滤波问题,并且不需要要求测量噪声必须服从高斯分布这样的制约条件。考虑到组合系统的非线性非高斯特性,现有的基于卡尔曼滤波器的故障检测方法已不再适用,针对这一问题,采用了基于粒子似然函数的故障检测方法。此外,针对不同的故障传感器,专门设计了不同的组合滤波模式,根据故障检测和隔离结果,选择适合的滤波模式,重构局部滤波结果,并在主滤波器中,进行全局滤波,最终获得全局最优估计。通过仿真分析,结果表明本文提出的多模式联邦高斯和粒子容错滤波技术是有效可行的。采用该技术,在各传感器子系统相继出现故障的情况下,INS/多天线GNSS/MHS/DNS组合导航系统仍然能够给出较高精度的导航信息。
参考文献:
[1]MaierA,KieselS,TrommerGF.PerformanceAnalysisofFederatedFilterforSAR/TRN/GPS/INSIntegration[J].GyroscopyandNavigation, 2011, 2(4): 293-300
[2]KazeronniM,KhayatianA.AMWPCA-BasedFaultDetectioninFederatednoResetModeFilter[C]∥Proceedingsof2012 20thIranianConferenceonElectricalEngineering,Piscataway,NY:IEEE, 2012:851-856
[3]赵琳, 班镜超. 组合导航联邦滤波故障检测技术研究[J]. 遥测遥控, 2014, 35(2): 9-13
ZhaoLin,BanJingchao.FederatedFilterFaultDetectionTechnologyResearchforIntegratedNavigation[J].JournalofTelemetry,TrackingandCommand, 2014, 35(2): 9-13 (inChinese)
[4]梁军,乔立岩,彭喜元. 基于SIR粒子滤波状态估计和残差平滑的故障检测算法[J]. 电子学报,2007, 35(12A): 32-38
LiangJun,QiaoLiyan,PengXiyuan.FaultDetectionBasedonSIRStateEstimationandSmoothedResidual[J].ActaElectronicaSinica, 2007, 35(12A): 32-38 (inChinese)
[5]葛哲学,杨拥民,胡政,等. 非高斯噪声下基于Unscented粒子滤波器的非线性系统故障诊断方法[J]. 兵工学报,2007, 28(3): 332-335
GeZhexue,YangYongmin,HuZheng,etal.UnscentedParticleFilter-BasedFaultDiagnosisofNon-LinearSystemwithNon-GaussianNoises[J].ActaArmamentarii, 2007, 28(3): 332-335 (inChinese)
[6]HuaminJia.DataFusionMethodologiesforMultisensorAircraftNavigationSystems[D].CranfieldUniversity, 2004
[7]KotechaJH,DjuricPM.GaussianSumParticleFiltering[J].IEEETransonSignalProcessing, 2003, 51(10): 2602-2612
[8]LyudmilaMihaylova,AndreasHegyi,AmadouGning,etal.ParallelizedParticleandGaussianSumParticleFiltersforLarge-ScaleFreewayTrafficSystems[J].IEEETransonIntelligentTransportationSystems, 2012, 13(1): 36-48
[9]PedrosaP,DinisR,NunesF,etal.PhaseNoiseEstimationforM-QAMConstellationsUsingGaussianSumParticleFiltering[C]∥IEEE79thVehicularTechnologyConference(VTCSpring), 2014:1-5
收稿日期:2015-10-27
作者简介:耿峰(1977—),西安导航技术研究所高级工程师,主要从事导航、制导与控制的研究。
中图分类号:V249
文献标志码:A
文章编号:1000-2758(2016)03-0449-07
Research on an Effective Integrated Navigation Failure-Tolerance Filtering Technology
Geng Feng1,2, Zhu Xiaoping2, Zhou Zhou3
1.Xi′an Research Institute of Navigation Technology, Xi′an 710068, China 2.365thResearch Institute, Northwestern Polytechnical University, Xi′an 710072, China 3.College of Aeronautics, Northwestern Polytechnical University, Xi′an 710072, China
Abstract:For an INS/multi-antenna GNSS/MHS/DNS integrated navigation system, the navigation information errors of one or more sensors may cause the positioning accuracy of the entire integrated navigation system in serious decline, and even could not make the system work as usual. In order to solve this problem, a multi-mode federated Gaussian sum particle fault-tolerant filtering technology is proposed. It adopts a no reset federated filter framework, and in the locally filtering, a Gaussian sum particle filter algorithm is utilized to improve the precision of filtering for nonlinear and non Gaussian system, meanwhile, a particle likelihood function failure detection algorithm is used to detect and isolate failure sensors. The simulation studies presented here show that the proposed multi-mode federated Gaussian sum particle fault-tolerant filtering technology is feasible, and the designed multi-mode integrated navigation filter can achieve sufficient reliability and accuracy.
Keywords:navigation, integration, fault tolerance, fault detection, sensors

