基于重叠场源法的非定常气动力计算研究

张辉, 李杰, 韩杰

(西北工业大学 航空学院, 陕西 西安　710072)



基于重叠场源法的非定常气动力计算研究

张辉, 李杰, 韩杰

(西北工业大学 航空学院, 陕西 西安710072)

摘要：面向气动弹性工程应用，将基于雷诺平均N-S方程的定常流动数值解引入跨声速小扰动方程，在小扰动条件下非定常激波效应由定常激波效应确定，从而发展了一种可用于跨声速流动的非定常气动力计算方法。数值算法利用块三对角近似技术大大提高了算法的计算效率、节省了计算所需内存空间，并采用了重叠场源策略为复杂构型的非定常气动力计算提供了有利保障。文中以F5机翼为计算算例，研究了场源模型参数对非定常气动力计算结果的影响，并验证了块三对角近似算法的可靠性；以CRM WBH翼身尾构型为算例，检验了针对复杂构型重叠场源策略的可行性。

关键词：非定常流动；跨声速流动；马赫数；气动力；压力分布；计算效率

非定常气动力的计算对气动弹性分析、动导数计算及机动、突风载荷计算等都具有特别重要的意义[1-3]。长期以来，广泛应用于气动弹性分析的气动力计算方法是偶极子格网法[4-5](doublet lattice method,DLM)，多个商用软件均采用了DLM进行气动弹性分析，如MSC.NASTRAN的气动弹性模块。DLM方法能够提供亚声速及超声速范围内较为精确的非定常气动力，其最大的优点还在于能够生成气动力影响系数(AIC)矩阵。AIC矩阵不依赖于飞机结构参数，因此，在结构设计循环中只需计算1次而重复使用。但是DLM是基于线化势流理论的方法，无法解决非线性较强的流场，不适用于跨声速非定常气动力计算。计算流体力学(CFD)方法通过求解Euler或Navier-Stokes方程能够给出精确的跨声速流场解，不过基于CFD的流场求解不能生成AIC矩阵，因而不能利用目前已经发展较完备的基于AIC矩阵的气动弹性分析方法。而目前用于气动弹性分析的CFD/CSD耦合计算方法[6-7]针对复杂飞机构型的适用性还有待发展，另外耦合算法需要巨大的计算资源和时间耗费，这样均不利于工程应用。因此，发展一种能够生成AIC矩阵的高效非定常跨声速气动力计算方法对跨声速范围内飞行器的气动弹性特性研究意义重大。

非定常场源方法即是一种能够生成AIC矩阵的方法，并且通过引入CFD定常解考虑了跨声速激波效应，从而适用于非定常跨声速气动力的计算。早在20世纪80年代，国外一些研究者就已经开始了对非定常场源法的研究，Larry L.Erickson和Shawn M.Strande[8]给出了利用场源法将面元方法推广以求解跨声速流动的理论基础；M.H.L Hounjet[9]研究了基于场源法和有限差分的混合方法求解非定常跨声速流动问题，该方法综合了有限差分和场源积分方法的优点，从而大幅地减少了计算时间，使得其可用于常规的颤振分析；Lutz Gebhardt和Dmitri Fokin等[10]研究了用于跨声速飞行器气动设计的场源方法，改进了自适应场源网格生成方法使得场源法的实际应用更加现实；Chen和Gao等[11]基于重叠场源策略通过求解关于时间线化的跨声速小扰动方程的积分方程生成非定常跨声速气动力影响系数矩阵，从而实现复杂构型的跨声速气弹分析，并利用块三对角近似技术求解大型的体单元影响系数矩阵，大大地提高了计算效率。然而，国内对基于场源法的跨声速非定常气动力计算的研究目前尚无公开发表的文献。

本文深入研究了非定常场源法的算法实现，将基于雷诺平均N-S方程的定常流动数值解引入跨声速小扰动方程，在小扰动条件下非定常激波效应由定常激波效应确定，从而发展了一种可用于跨声速流动的非定常气动力计算方法。

1非定常场源法的求解方程

关于结构振荡幅值线化非线性跨声速小扰动方程得到时间线化的跨声速小扰动速势方程如下：

(1)

(2)

φs表示表面面元强度对速度势的影响，可写为

(3)

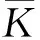
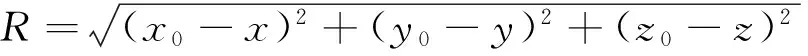
(4)

(5)

式中，Δσv表示穿过激波面体源强度的跳跃。当不存在跨声速激波时，Δσv=0,φshock自动消失。另外，当激波出现时，也可通过对φv完成如下分部积分运算以消掉φshock。

(6)

得到

(7)

式中，xs表示激波位置，ε表示激波面无限小厚度。由(5)式和(7)式可得

(8)

2定常流动数值解的引入

本文用于求解定常流动数值解的控制方程如下

(9)

式中，Q=(ρ,ρu,ρv,ρw,ρe)T为守恒向量；ρ、e、(u,v,w)分别为密度、单位质量气体的总能量和直角坐标系下的速度分量；v为控制体体积；s为控制体表面积；F为通过表面s的黏性通量和无黏通量的和；n为边界外法向单位矢量。黏性项采用中心差分格式离散，无黏项采用Roe三阶迎风偏置通量差分裂方法离散，采用隐式近似因子分解(AF)方法进行时间推进，选用SA湍流模型，通过多重网格技术来加速收敛。

采用场源法求解非定常气动力时，需要建立场源模型，场源模型包括面单元和体单元。首先建立面元气动模型，通常将飞机部件分为翼面类和机身类部件处理，翼面类部件由位于翼面类部件均平面的非定常涡面来模拟，机身类部件表面离散为体表面单元，每个体表面单元上布置非定常源，以模拟由于体的体积效应产生的气动力分布；其次围绕翼面类部件(升力面)或机身类部件的面元气动模型定义体块，然后将体块分割为若干体单元。场源模型建立后，即可将上述定常流场数值结果(包括当地马赫数及扰动速度分量)插值到每个体单元上。建立合适的场源模型直接决定着插值精度，进而影响最终非定常气动力计算的精度。在建立场源模型时，确保场源模型中的物面边界尽可能与CFD计算模型的物面边界重合是建立合适的场源模型的必要条件。此外，体块高度和体块分割层数是场源模型的2个重要参数，这2个参数的选取对计算结果有重要影响，选择的依据是确保场源模型包含非线性流动区域。算例验证部分详细研究了体块高度和体块分割层数对计算结果的影响，并归纳总结了体块高度和体块分割层数选取的一些原则。

3AIC矩阵的生成及算法策略

3.1AIC矩阵的生成

位于面单元控制点处的法向扰动速度为

(10)

体单元控制点处的速度势为

(11)

式中，矩阵[A]和[C]分别为面奇点对面单元和体单元的影响系数矩阵，矩阵[B]和[D]分别为体源对面单元和体单元的影响系数矩阵。引入如下有限差分算子[T]

(12)

将方程(12)代入(10)式和(11)式，得到

(13)

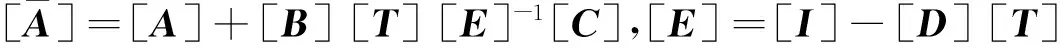
3.2块三对角近似技术

上节中矩阵[E]为满系数复数矩阵，其阶数与体单元数相同。对于简单的三维问题需要较多体单元数，并且体单元数随构型复杂程度的增加而急剧增加。这种大型矩阵求逆对常规的气弹及载荷分析是不实用的。因此，有必要采用块三对角近似技术解决大型满系数矩阵[E]求逆的问题。块三对角近似技术的思路[11]是：首先体单元被分为许多子块，同一个子块内的体单元组合在一起。这样矩阵[E]可写为

(14)

式中，[EB]为块三角矩阵，其三角块包含自身块和相邻子块的影响系数；[Eε]包含三角块处的零元素和非相邻块的影响系数。下一步比较矩阵[Eε]和矩阵[EB]内系数的量级，可以看出[Eε]内所有系数均是小量，原因是方程(4)的积分方程的积分函数包含1/R函数，当点(x0,y0,z0)远离非相邻子块时，1/R快速衰减。因此，矩阵[E]的逆可由下式近似

(15)

因为[EB]为块三角矩阵，所以[EB]-1可利用块三角矩阵求解技术有效计算。

3.3针对复杂构型的重叠场源策略

针对复杂飞机构型，本文采用重叠场源策略以减小网格生成的难度，减少计算所需内存并节省计算时间。首先针对复杂构型的每一个部件独立生成体单元网格，然后基于以下原则[11]构建这种重叠体单元模型的影响系数矩阵：①不同体块内的体单元互不影响；②同一个体块内的体单元仅影响与其相关联的面元；③所有面元影响所有体单元。

4算例验证

4.1F5机翼

本节以F5机翼[12]为算例，建立不同参数下的场源模型，取计算马赫数为0.90，减缩频率为0.275，进行计算分析并与实验值对比以研究场源模型不同参数对非定常气动力计算精度的影响。主要研究了场源模型的体块高度H、体块分割层数Nl、体块前(后)缘向前(后)延伸量EXT及分割数Ne对非定常气动力计算精度的影响。以机翼根弦长C为参考，分别取体块高度0.25C、0.50C、1.00C和1.50C，保持其他参数不变，其中体块层数为7。计算所得展向51.5%位置处非定常压力系数结果与实验值对比如图1所示，当体块高度较小，如H=0.25C和0.50C时，计算结果明显小于实验值，计算对激波强度的预测明显偏小；随着体块高度的增加，在H=1.00C时，计算结果与实验值比较接近，计算精度较好；随着体块高度的继续增加，在H=1.50C时，计算结果则高于实验值，显然这不是一个理想的结果，因为这与之前的理论分析相悖，按照理论分析当H=1.50C时其场源模型比其他场源模型大，所以合理的结果应该是此时的计算结果应更加接近实验值，但图2结果并非如此。进一步，保持体块高度为H=1.50C，选取体块层数分别为5、7、9、11完成计算，同样给出展向51.5%位置处非定常压力系数的计算结果与实验值对比如图2所示，对比结果表明，随着体块层数的增加，计算结果不断逼近实验值，并且Nl=11对应的计算结果略好于图1中体块高度H=1.00C的计算结果。因此，可以得到如下结论：①增大场源模型以确保场源模型包含非线性流动区域可以提高非定常气动力的计算精度；②若保持其他参数不变，只是增大体块高度会使非定常气动力的计算精度变差，原因是随着体块高度的不断增加，使得体单元分布越来越稀疏，过于稀疏的体单元分布降低了其计算精度；③保持其他参数不变，增加体块层数，计算结果趋于收敛；另外，图3给出了一个状态所需的CPU计算时间随体单元个数的变化曲线，可见CPU计算时间随着体单元数的增加呈指数式增加。因此，为了兼顾精度与效率，对于该算例，选取体块高度为1.0C，体块层数为7较合适。

图1　体块高度的影响　　　　　　　图2　体块分割层数的影响图3　计算时间随体单元数的变化

取体块高度为1.0C，体块层数为7，分别选取体块前(后)缘向前(后)延伸量EXT为0.00C、0.10C、0.25C、0.50C的场源模型进行计算，计算结果与实验值对比如图4所示，可见随着延伸量EXT的增加，计算结果向实验值靠近，但变化量很小。图5给出了延伸段不同分割数的场源模型计算结果对比，可以看到分割数分别为2、4、6时，计算结果基本重合，表明该处分割数对计算结果几乎没有影响。

针对F5机翼，分别建立单块场源模型和多块场源模型，对于多块场源模型，利用块三对角近似技术进行求解，对比2种场源模型计算结果，验证块三对角近似的可靠性。图6给出了机翼展向51.5%位置处压力分布对比结果，可见三对角近似求解结果与单独体块求解结果基本重合，这表明了三对角近似求解是可靠的。此外，与单独体块求解相比，块三对角近似求解节省了大约40%的CPU计算时间。

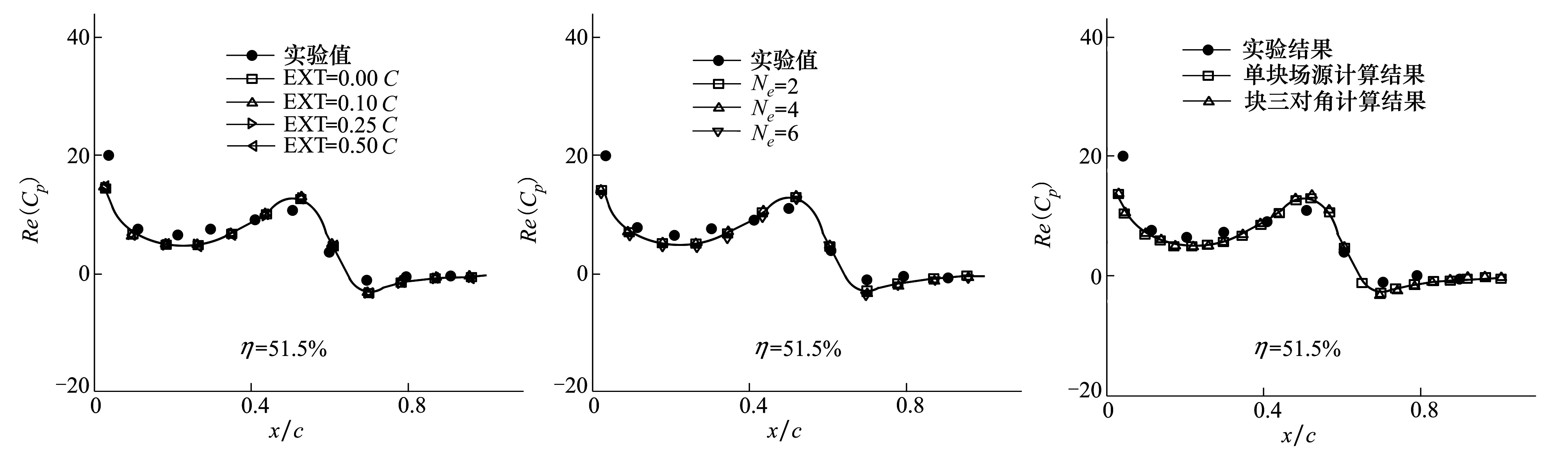
图4　场源模型前后延伸量的影响　　　图5　延伸段分割数的影响　　　图6　块三对角近似技术的验证，k=0.275

4.2CRM WBH翼身尾构型

采用重叠场源策略建立CRM WBH飞机构型[13]场源模型，分别针对机翼、平尾、机身独立生成体块，每个体块被分割为若干子块生成体单元网格以应用块三对角近似技术求解。根据上节研究结论，机翼和平尾对应体块高度取各自的根弦长，体块层数为7，机身对应体块高度取为机身中段半径长，体块层数为8，建立场源模型如图7所示。

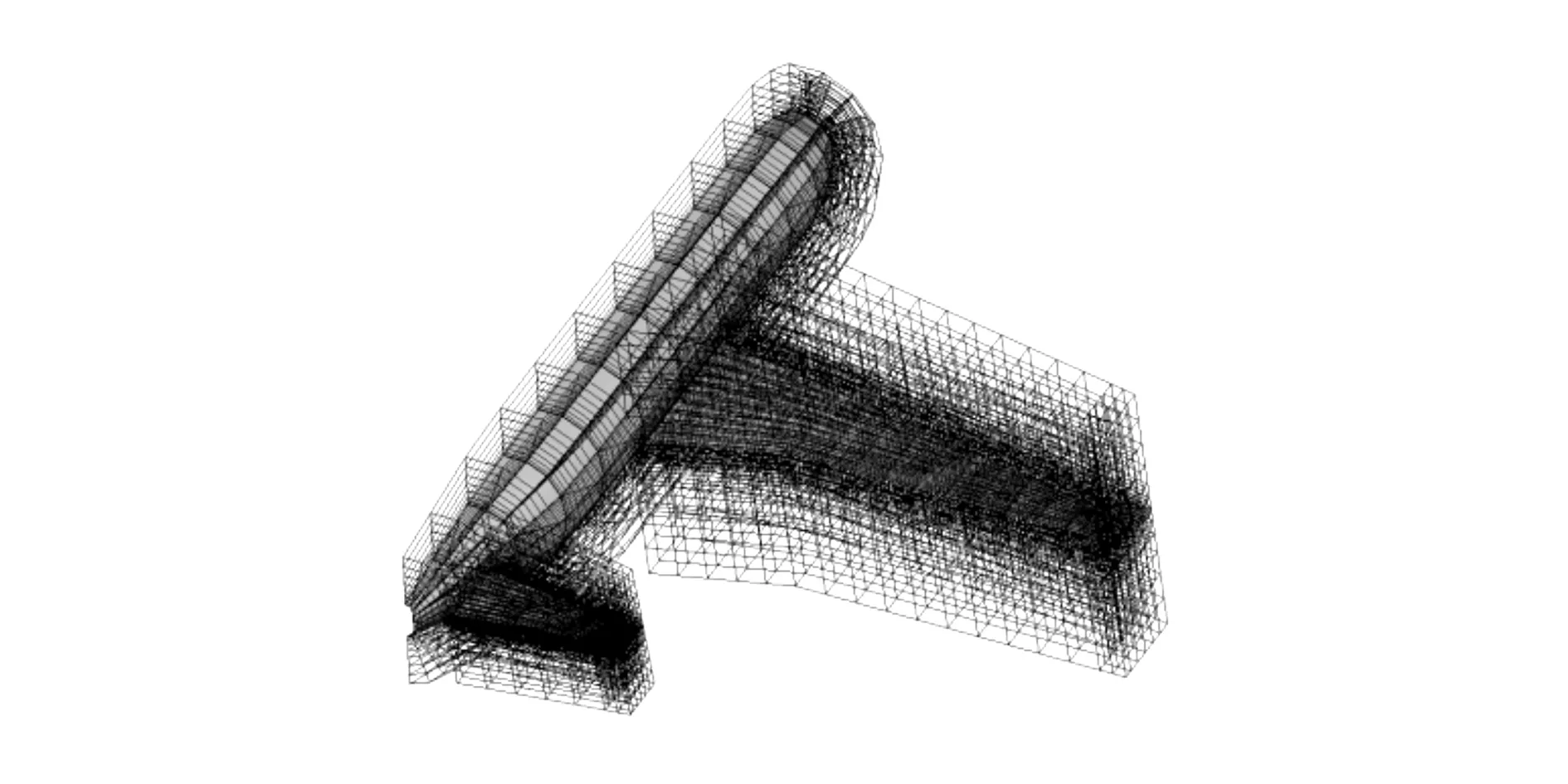
图7　CRM WBH构型场源模型

取计算马赫数0.85，减缩频率0.15进行计算。图8给出了CRM WBH 构型俯仰振荡模态时机翼展向50.2%处翼面非定常压力分布对比结果。由于没有实验结果，本文以ZAERO软件[14]的跨声速方法计算结果作为参考验证本文计算方法的可靠性，对比可见本文计算结果与ZAERO计算结果基本一致，仅在对激波强度的预测方面稍有差异，这说明了针对复杂飞机构型本文采用的重叠场源策略是可靠的。同时图中给出了偶极子格网法的计算结果，显然，由于偶极子格网法不能考虑跨声速激波效应的影响，而对于当前计算状态下机翼翼面展向50.2%位置处存在较强激波的状况，偶极子格网法计算结果必然与考虑了跨声速激波效应的计算方法所得结果存在较大差异。换言之，如果翼面不存在激波，也不存在流动分离，那么偶极子格网法计算结果就应该与本文气动力方法计算结果接近。平尾翼面压力分布对比结果有利地证实了这一点。图9给出了俯仰振荡模态时平尾展向50%处翼面非定常压力分布对比结果。图9中本文气动力方法、偶极子格网法及ZAERO跨声速方法计算结果可以看到，3种计算方法所得结果基本一致。

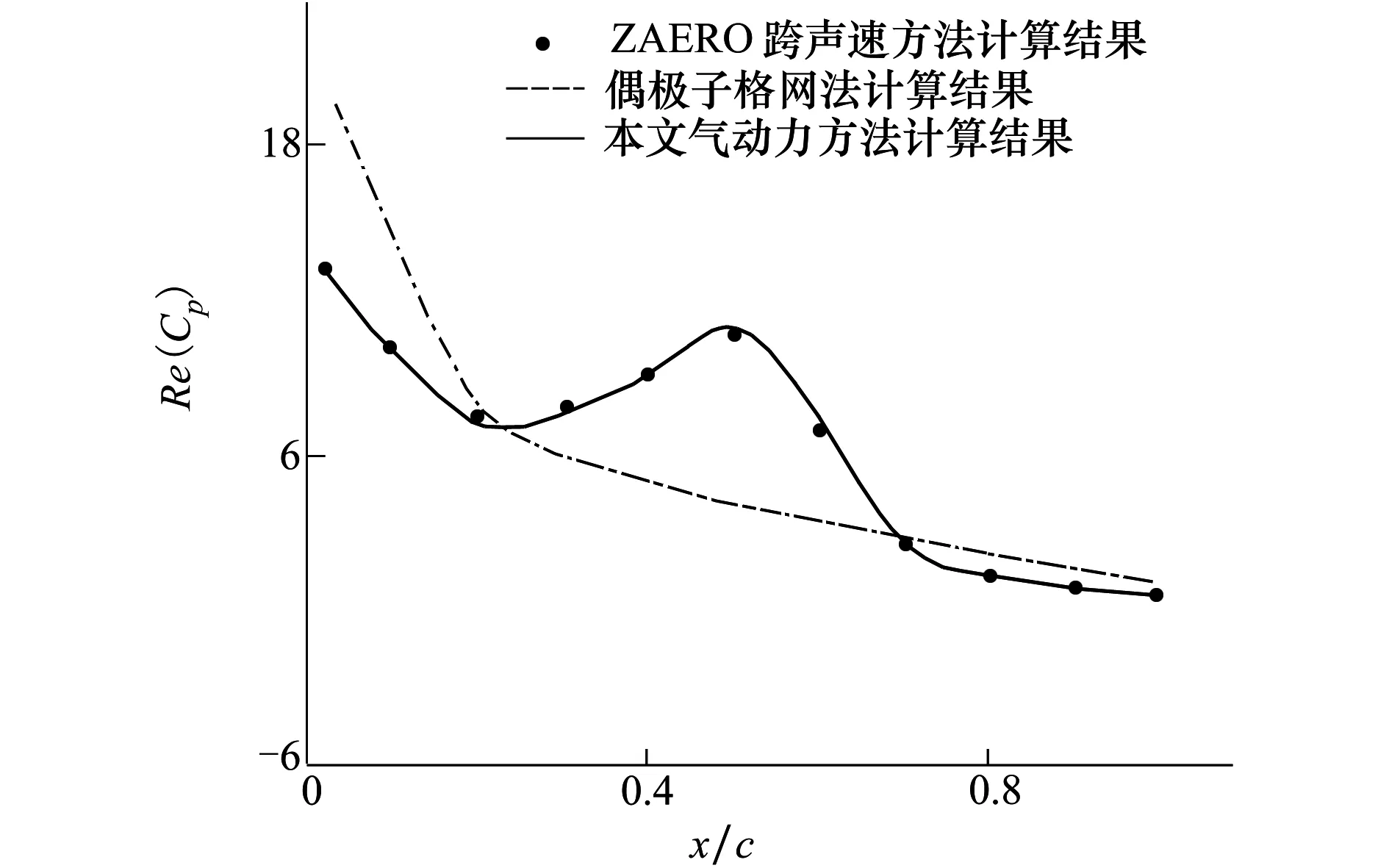
图8　机翼展向50.2%处非定常压力系数

图9　平尾展向50%处非定常压力系数

5结论

本文通过引入CFD定常解考虑跨声速激波效应，面向气动弹性分析发展了一种跨声速非定常气动力计算方法。文中以F5机翼为算例研究了场源模型参数对非定常气动力计算结果的影响，得到了选择合适场源模型的一般规律，并验证了块三对角近似算法的可靠性；以CRM WBH翼身尾构型为计算算例，单块和多块场源模型计算结果的对比表明针对复杂构型重叠场源策略是可行性的。算例计算结果与实验及参考文献结果的对比分析表明本文发展的方法适用于跨声速非定常气动力的计算。

参考文献：

[1]Rafael N, Joao L. Comparison of Viscous and Inviscid Unsteady Aerodynamic Loads for Aeroelastic Analysis[R]. AIAA-2015-0767

[2]Hyungro Lee, Beom-Soo Kim, et al, Computational Study of the Stability Derivatives for the Standard Dynamic Model[R]. AIAA-2013-2658

[3]Leonard M, Ilhan T. Time Simulations of the Response of Maneuvering Flexible Aircraft[J]. Journal of Guidance, and Dynamics, 2004, 27(5): 814-828

[4]Albano E, Rodden W P. A Doublet-Lattice Method for Calculating Lift Distributions on Oscillating Surfaces in Subsonic Flows[J]. AIAA Journal, 1969, 7(2): 279-285

[5]管德. 非定常空气动力学计算[J]. 北京：北京航空航天大学出版社，1991

Guan De. Calculation on Unsteady Aerodynamics[M]. Beijing, Beijing University of Aeronautics and Astronautics Press, 1991 (in Chinese)

[6]徐敏，安效民，陈士橹．一种CFD/CSD耦合计算方法[J]．航空学报，2006, 27(1)：33-37

Xu Min, An Xiaomin, Chen Shilu. CFD/CSD Couping Numerical Computational Methodology[J]. Acta Aeronautica et Astronautica Sinica, 2006, 27(1): 33-37 (in Chinese)

[7]Giulio Romanelli, Michele Castellani, Paolo Mantegazza, et al, Coupled CSD/CFD Non-Linear Aeroelastic Trim of Free-Flying Flexible Aircraft[R]. AIAA-2012-1562

[8]Erickson Larry L, Strande Shawn M. A Theoretical Basis for Extending Surface Paneling Methods to Transonic Flow[J]. AIAA Journal, 1985, 23(12): 1860-1867

[9]Hounjet M H L. A Field Panel/Finite Difference Method for Potential Unsteady Transonic Flow[J]. AIAA Journal, 1985, 23(4): 537-545

[10] Gebhardt Lutz, Fokin Dmitri, Lutz Thorsten, et al. An Implicit-Explicit Dirichlet-Based Field Panel Method for Transonic Aircraft Design[R]. AIAA-2002-3145

[11] Chen P C, Gao X W, Tang L. Overset Field-Panel Method for Unsteady Transonic Aerodynamic Influence Coefficient Matrix Generation[J]. AIAA Journal, 2004, 42(9): 1775-1787

[12] Malone J B, Sankar N L, et al. Unsteady Aerodynamic Modeling of a Fighter Wing in Transonic Flow[R]. AIAA-1984-1566

[13] John C, Edward N. Summary of the Fourth AIAA CFD Drag Prediction Workshop[R]. AIAA-2010-4547

[14] ZAERO Theoretical Manual[M]. ZONA Technology Inc Scottsdale, 2008

收稿日期：2015-10-22

基金项目：国家自然科学基金(11172240)、国家重点基础研究发展计划(2015CB755800)与航空科学基金(2014ZA53002)资助

作者简介：张辉(1986—)，西北工业大学博士研究生，主要从事理论与计算流体力学研究。

中图分类号：V215

文献标志码：A

文章编号:1000-2758(2016)03-0443-06

Calculation of Unsteady Aerodynamics Using Overset Field-Panel Method

Zhang Hui, Li Jie, Han Jie

(College of Aeronautics, Northwestern Polytechnical University, Xi′an 710072, China)

Abstract:The paper present a method of calculating unsteady aerodynamics in transonic flow, in which steady flow solution based on RANS solver code are imported into transonic small disturbance equations, thus, the unsteady shock location is dominated by the steady shock location in the small amplitude sense. Block-tridiagonal approximation is used to improve the computational efficiency and save the memory, and the overset field panel scheme is developed for complex configuration to calculate unsteady aerodynamics. Taking F5 wing as an example, the effect of parameters of field-panel model on the calculated results of unsteady aerodynamics is investigated, and the reliability of block-tridiagonal approximation is validated. In addition, the validation of overset field-panel scheme is performed by comparing the results between the one block modeling and the overset modeling.

Keywords:unsteady flow; transonic flow; Mach number; aerodynamics; pressure distribution; computational efficiency