基于分层模型的非定常气动力建模研究

周 萌 高国柱

(中国电子科技集团公司第三十八研究所浮空平台部，安徽 合肥 230088)

0 引言

在气动弹性问题[1]，如极限环特性问题研究中，既存在小幅值振荡，又存在大幅值振荡。 对于小幅值振荡，气动力与模态位移呈现动态性关系；而随着振幅不断增加，流场和非定常气动力逐渐呈现出明显的非线性特征。此时需要构建既兼顾线性又兼顾非线性特征的非定常气动力模型。

在线性气动力降阶模型中，Attar 等[2]通过研究，构建了能够描述一定非线性的ARMA 线性降阶模型。

随着线性气动力降阶模型技术的发展，多种代理模型技术也开始用于构建非定常流场降阶模型，典型的有各种响应面技术（如Kriging 代理模型和RSM 多项式响应面技术等） 和神经网络（如BP 神经网络和RBF 神经网络和小波神经网络等）。如刘艳[3]等建立一种基于改进Kriging 插值建立KSBRF 降阶模型，用于预测非线性下的非定常气动力及力矩等。

Kriging 模型[4]由于其对非线性函数的良好近似能力和独特的误差估计功能，正受到越来越多研究者的关注。

因此， 本文采用线性的ARAM 模型和非线性的Kriging 模型建立非定常气动力降阶模型。

1 分层降阶模型

分层降阶模型的核心是在建立非线性模型时，需要获取的第k+1 步的线性部分气动力是由第k 步的大幅位移和第k 步的线性气动力作为输入， 也就是说， 其输入的气动力时由线性模型ARMA 迭代得到的。 然后采用大幅位移和气动力差量（大幅值气动力响应减去获取线性部分气动力）作为输入，将气动力的差量作为目标建立非线性部分的模型如图1 所示。

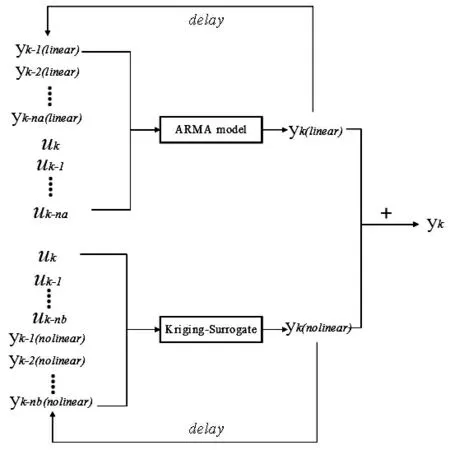
图1 分层降阶模型

u（包含俯仰模态α 和浮沉模态h/b）表示输入的激励信号，即模态位移。y（包含气动升力CL 和俯仰力矩Cm）表示通过CFD 计算得到的非定常气动力。 uk表示第k 步输入的模态位移，uk-na 表示第k-na 步输入的模态位移，yk 表示第k 步得到的气动力yk-na 表示第k-na 步得到的气动力，其他符号类似。 其中ARMA 模型在文献[2]中已得到验证。

2 非定常气动力模型建立

图2 采用两组不同幅值的训练信号对分层模型进行训练，两组信号均由随机过滤高斯白噪声信号得到。 从设计的信号形状可以看出，无论是大幅还是小幅训练信号，每个模态位移都具有较宽的频率范围和足够的幅值信息，因此，可以用于较宽频率、振幅下的非定常气动力预测。

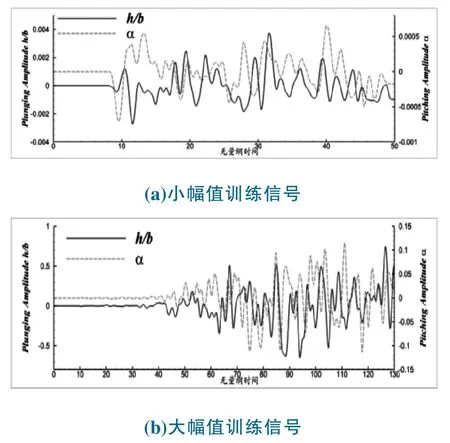
图2 训练信号

图3 非线性分层模型对训练信号的辨识结果

第一组是小幅激励信号， 用于训练动态线性的ARMA 模型。

第二组是大幅激励信号，其气动力响应与ARMA模型在相同运动下得到的输出相减，作为非线性部分的气动力输出，用于训练Kriging 代理模型。

3 结语

本文建立了一种兼顾线性和非线性特征的分层气动力模型，并采用扫频测试信号验证了气动力计算精度。