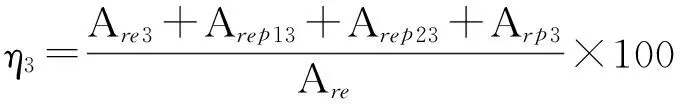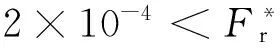尺度相关的分形粗糙表面弹塑性接触力学模型

成雨, 原园, 甘立, 徐颖强, 李万钟

(1.西安理工大学 机械与精密仪器工程学院, 陕西 西安　710048;2.西北工业大学 机电学院, 陕西 西安　710072)



尺度相关的分形粗糙表面弹塑性接触力学模型

成雨1, 原园1, 甘立1, 徐颖强2, 李万钟2

(1.西安理工大学 机械与精密仪器工程学院, 陕西 西安710048;2.西北工业大学 机电学院, 陕西 西安710072)

摘要：依据分形理论,研究了粗糙表面间的真实接触状况,建立了粗糙表面间的分形接触模型。考虑微凸体的等级,确定了弹性临界等级、第一弹塑性临界等级和第二弹塑性临界等级的表达式,研究了粗糙表面中单个微凸体的弹性、弹塑性及完全塑性变形的存在条件,推导出各个等级微凸体的临界接触面积的解析式。在此基础上应用微凸体的面积分布密度函数,获得了接触表面上接触载荷与真实接触面积之间的关系。计算结果表明:单个微凸体的临界接触面积是和微凸体的尺度相关,随着微凸体等级的增大而减小;微凸体的变形顺序为弹性变形、弹塑性变形和完全塑性变形,与传统的接触模型一致;在整个粗糙表面接触过程中,粗糙表面变形过程与单个微凸体的变形过程一致;最大微凸体所处的等级范围不同,粗糙表面所表现的力学性能也不相同。

关键词：粗糙表面;微凸体;尺度;临界接触面积;弹塑性接触

粗糙表面间接触特性的研究对分析其摩擦、磨损、导电、导热等性能具有重要影响。早期的研究主要是基于统计学分析的接触模型,采用的统计参数与采样长度和仪器分辨率相关,进而导致对确定粗糙表面的表征和分析结果不具有唯一性[1-2]。分形几何理论提出后,迅速应用到粗糙表面的接触问题,利用分形理论建立的粗糙表面接触模型可以提供多尺度的接触行为预测分析。Majumdar等[3]提出以分形几何为基础的分形接触模型(MB模型),但该模型中未考虑微凸体的弹塑性变形,认为微凸体的临界弹性接触面积与尺度无关,得到接触过程中微凸体先发生塑性变形,后发生弹性变形,这一结果与传统的接触力学结果相反;Kogut等[4]用有限元法分析了粗糙表面上单个球状微凸体与刚性平面的接触情况(KE模型);Morag等[5]基于分形模型,应用Hertz理论证明了微凸体的临界接触面积与微凸体的尺寸相关,推导出了接触变形过程中微凸体先发生弹性变形,再发生非弹性变形;然而上述2种模型都只研究了粗糙表面上单个微凸体的变形机制,并没有考虑整个粗糙表面上的接触载荷与真实接触面积之间的关系。Liou等[6]研究了柱状粗糙表面与刚性光滑平面的接触,同样得到了随着变形量的不断增加,微凸体先发生弹性变形,再发生弹塑性变形或是完全塑性变形;缪小梅和丁雪兴等[7-8]依据分形理论也推导出了单个微凸体的弹性临界接触面积与微凸体的尺度相关。基于上述研究现状,依据分形理论,考虑微凸体的等级,确定了弹性临界等级、第一弹塑性临界等级和第二弹塑性临界等级的表达式,研究单个微凸体的力学特性,确定了不同等级微凸体的弹性临界接触面积、第一弹塑性临界接触面积和第二弹塑性临界接触面积。结合海洋岛屿面积分布规律建立了粗糙表面弹塑性接触力学模型,获得了不同等级微凸体下整个粗糙表面上接触总载荷与真实接触面积之间的关系。

1粗糙表面几何模型的建立

粗糙表面具有自仿射与多尺度的分形特性,Majumdar等[3]用Weierstrass-Mandelbrot函数(W-M函数)来表征粗糙表面二维轮廓曲线,表达式如下

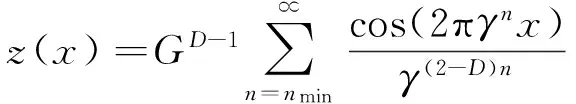
(1)

式中,z(x)表示粗糙表面轮廓曲线的高度;x为轮廓的位移坐标;D为表面轮廓分形维数;G为轮廓特征尺度系数;γ为大于1的常数,对于服从正态分布的表面,取γ=1.5[3,5];γn表示轮廓曲线的空间频率,nmin为与轮廓结构最低截止频率对应的序数。

轮廓曲线由D、G和nmin3个参数决定,由于表面轮廓为非平稳的随机过程,最低截止频率跟取样长度有关,D和G可由二维W-M函数的功率谱获得。

2两粗糙表面接触

两粗糙表面间的接触可以等效为一个粗糙表面与一个刚性光滑平面的接触,且等效粗糙表面满足各向同性的分形特性;忽略接触过程中微凸体之间的相互作用;假设变形时只有微凸体发生变形且不考虑接触过程中接触硬化和硬度随深度的变化;不考虑摩擦。

2.1单个微凸体力学模型的建立

粗糙表面是由一系列不同尺寸的余弦波状微凸体叠加而成的,对于任何一个微凸体l=1/γn,变形前的轮廓曲线可定义为

(2)

图1为单个接触微凸体变形示意图,其中l为微凸体基底的尺寸,δ为微凸体的幅值,ω为实际变形量,取值范围为0≤ω≤δ,具体大小与所受载荷有关,l′为用一刚性平面截微凸体所得的截断长度,lr为微凸体变形量为ω时的实际接触长度。

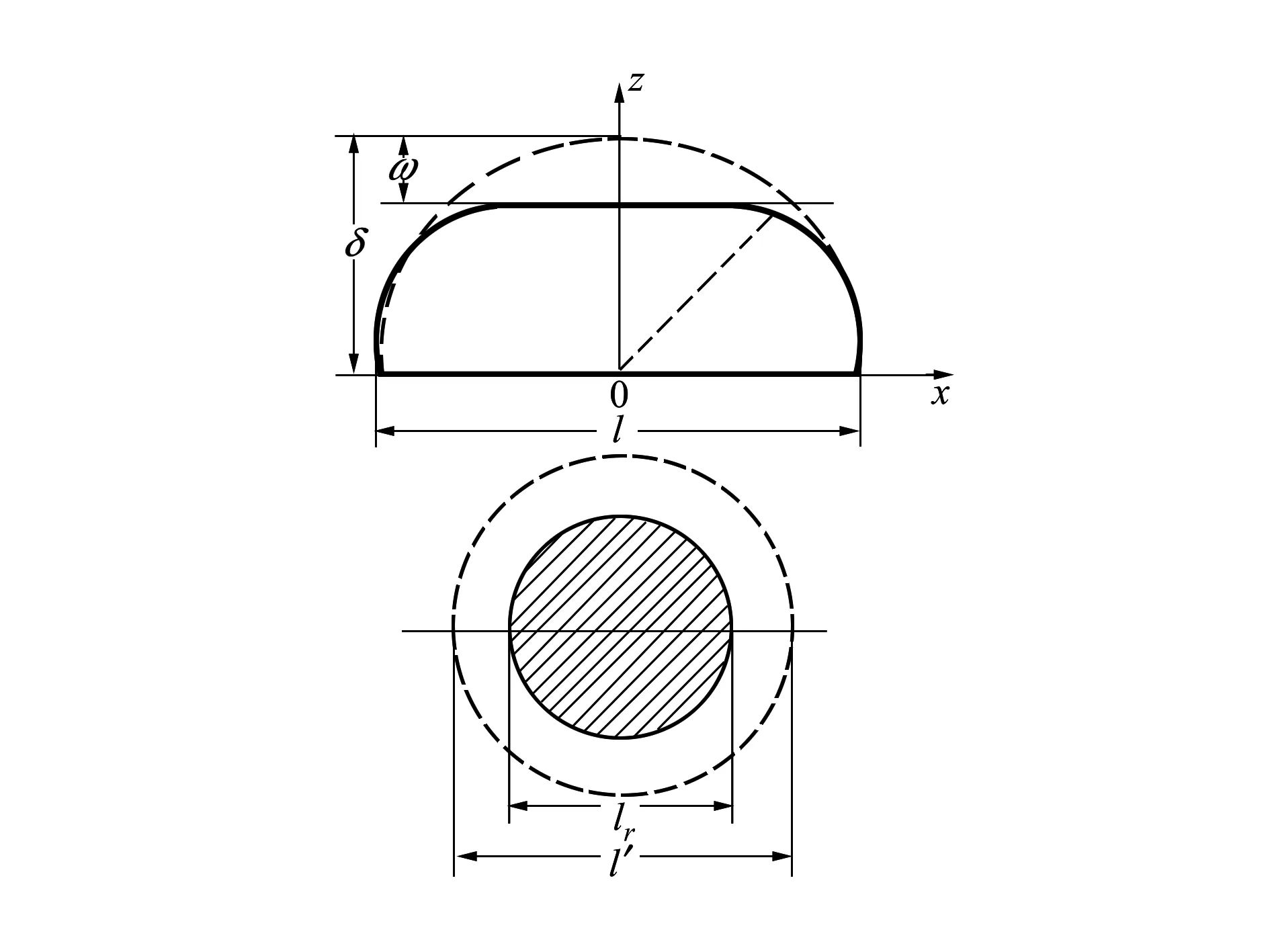
图1　接触微凸体变形示意图

由(2)式可得微凸体顶端曲率半径R为

(3)

由(2)式可得微凸体的幅值δ为

(4)

当截断长度为l′时,微凸体的实际变形量ω为

(5)

2.2微凸体的变形机制

两粗糙表面接触过程中,随着变形量的不断增加,表面上的微凸体可能存在3种变形状态,分别为弹性变形、弹塑性变形和完全塑性变形。下面分别讨论单个微凸体处于3种不同变形状态时的接触面积和接触载荷。

2.2.1弹性变形状态存在条件

根据Hertz理论[9],将开始塑性变形的临界变形量为

(6)

式中，H为较软材料的硬度,K为硬度系数,与材料的泊松比v相关,满足K=0.454+0.41v,E为等效弹性模量,φ=H/E为材料属性。

当ω≤ωec时,微凸体发生弹性变形,由Hertz理论可得,单个微凸体的接触面积a和接触载荷F分别为

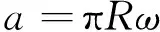
(7)

(8)

当微凸体变形量为ωec时,可认为微凸体处于弹性变形范围内,由(7)式可知,微凸体的弹性临界接触面积为

(9)

对比(7)式和(9)式可得:当ω≤ωec时,有a≤aec,即单个微凸体的接触面积小于或等于弹性临界接触面积时发生弹性变形。

联立(7)式和(8)式得单个微凸体发生弹性变形时,接触载荷F与接触面积a之间的关系为

(10)

由(10)式可知,单个微凸体发生弹性变形时,接触载荷与接触面积的3/2次方成正比。

2.2.2弹塑性变形状态存在条件

Kogut等[4]研究了粗糙表面单峰接触的力学特性,结果表明:当ωec<ω≤110ωec时,接触微凸体发生弹塑性变形,并将微凸体的弹塑性变形分为2个区域:

第一弹塑性变形区(ωec<ω≤6ωec)

(11)

第二弹塑性变形区(6ωec<ω≤110ωec)

(12)

易得第一弹塑性和第二弹塑性的临界变形量分别为

(13)

(14)

将(6)式、(8)式和(9)式代入(11)式和(12)式中,可得单个微凸体发生弹塑性变形时,接触载荷F与接触面积a之间的关系为

(15)

(16)

式中，aepc和apc分别为第一弹塑性临界接触面积和第二弹塑性临界接触面积,其大小分别为aepc=7.119 7aec、apc=205.382 7aec由(15)式和(16)式可知,单个微凸体发生弹塑性变形时,接触载荷与接触面积近似成线性关系。

2.2.3完全塑性变形存在条件

当ω>ωpc时,微凸体发生完全塑性变形,接触面积a和接触载荷F的表达式如下

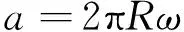
(17)

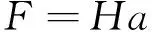
(18)

综上所述,单个微凸体的临界接触面积(弹性临界接触面积、第一弹塑性临界接触面积和第二弹塑性临界接触面积)是尺度相关的,符合经典赫兹接触理论[7],与传统的分形接触模型不同。对于确定的材料属性和分形参数,微凸体临界弹性接触面积与微凸体的等级成反比。任一微凸体受力发生变形,接触面积a满足:a≤aec时为弹性变形;aecapc时为完全塑性变形。

2.3微凸体等级n的计算

当δ≤ωec,微凸体发生弹性变形,即:

可求得弹性临界等级为

(19)

式中，fix表示取整

同理可以得到第一弹塑性临界等级nepc为

(20)

第二弹塑性临界等级npc为

(21)

综上所述,当nmin≤n≤nec时,微凸体只发生弹性变形;当necnpc时,微凸体发生弹性变形、第一弹塑性变形、第二弹塑性变形和完全塑性变形。

2.4微凸体的面积分布密度函数

Wang和Komvopoulos等[10]在修正的M-B分形接触模型中指出,分形粗糙表面与刚性光滑平面接触时,微凸体的接触面积分布密度函数为

(22)

真实接触面积Ar为

(23)

式中，al为最大微凸体的接触面积,φ为分形区域扩展系数,与轮廓分形维数D之间的函数表达式[8]为

(24)

2.5真实接触面积和接触载荷

两粗糙表面接触时的真实接触面积Ar和总的接触载荷Fr是所有接触微凸体的接触面积和接触载荷的总和,计算如下

真实接触面积为

(25)

式中，Are为弹性变形部分的接触面积,Arep1为第一弹塑性变形部分的接触面积,Arep2为第二弹塑性变形部分的接触面积,Arp为完全塑性变形部分的接触面积。下面分别计算这四部分的真实接触面积。

(26)

(27)

(28)

(29)

总的接触载荷为

(30)

同理,Fre为弹性变形部分接触载荷,Frep1为第一弹塑性变形部分接触载荷,Frep2为第二弹塑性变形部分接触载荷,Frp为完全塑性变形部分接触载荷。

(31)

(32)

(33)

(34)

将(31)～(34)式代入(30)式并进行无量纲化处理即两边同时除以EAa,可得总的接触载荷与真实接触面积之间的无量纲关系

(35)

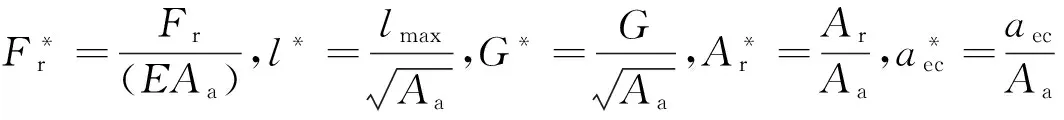
由于单个微凸体临界接触面积的尺度相关性,在求解真实接触面积和接触载荷过程中,临界接触面积选取影响结果的准确性,在本文中我们选择最大微凸体的临界接触面积(对应等级n最小)来计算整个粗糙表面的接触载荷和真实接触面积,以下对其误差进行分析。计算参数选取D=1.5,G=2.5×10-9m,φ=0.001。

1) 当所有微凸体都处于同种变形状态时,同时处于弹性变形状态、第一弹塑性变形状态、第二弹塑性变形状态或完全塑性变形状态。粗糙表面的真实接触面积和接触载荷可以用最大微凸体的临界接触接触面积来计算[7]。

(36)

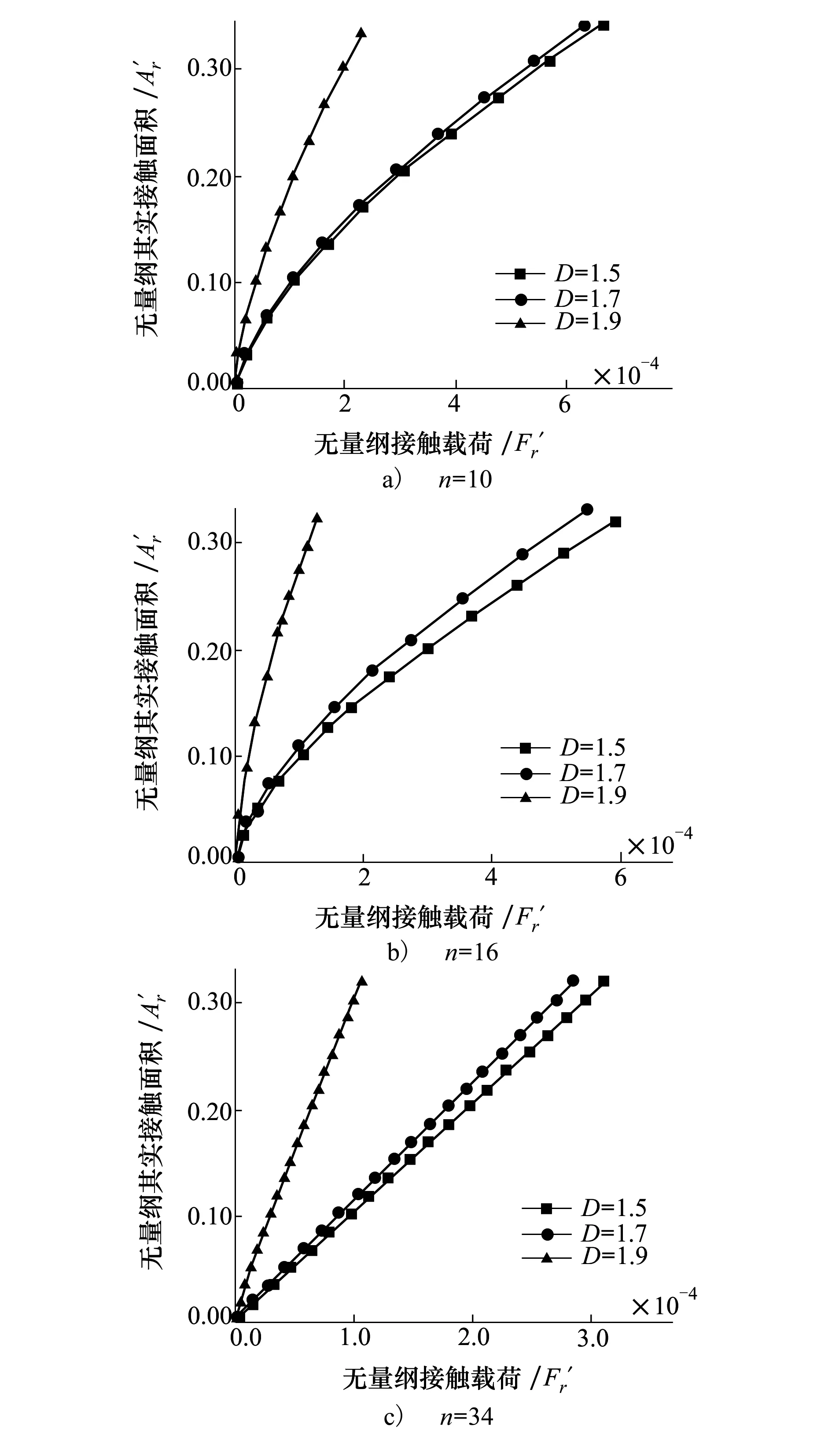
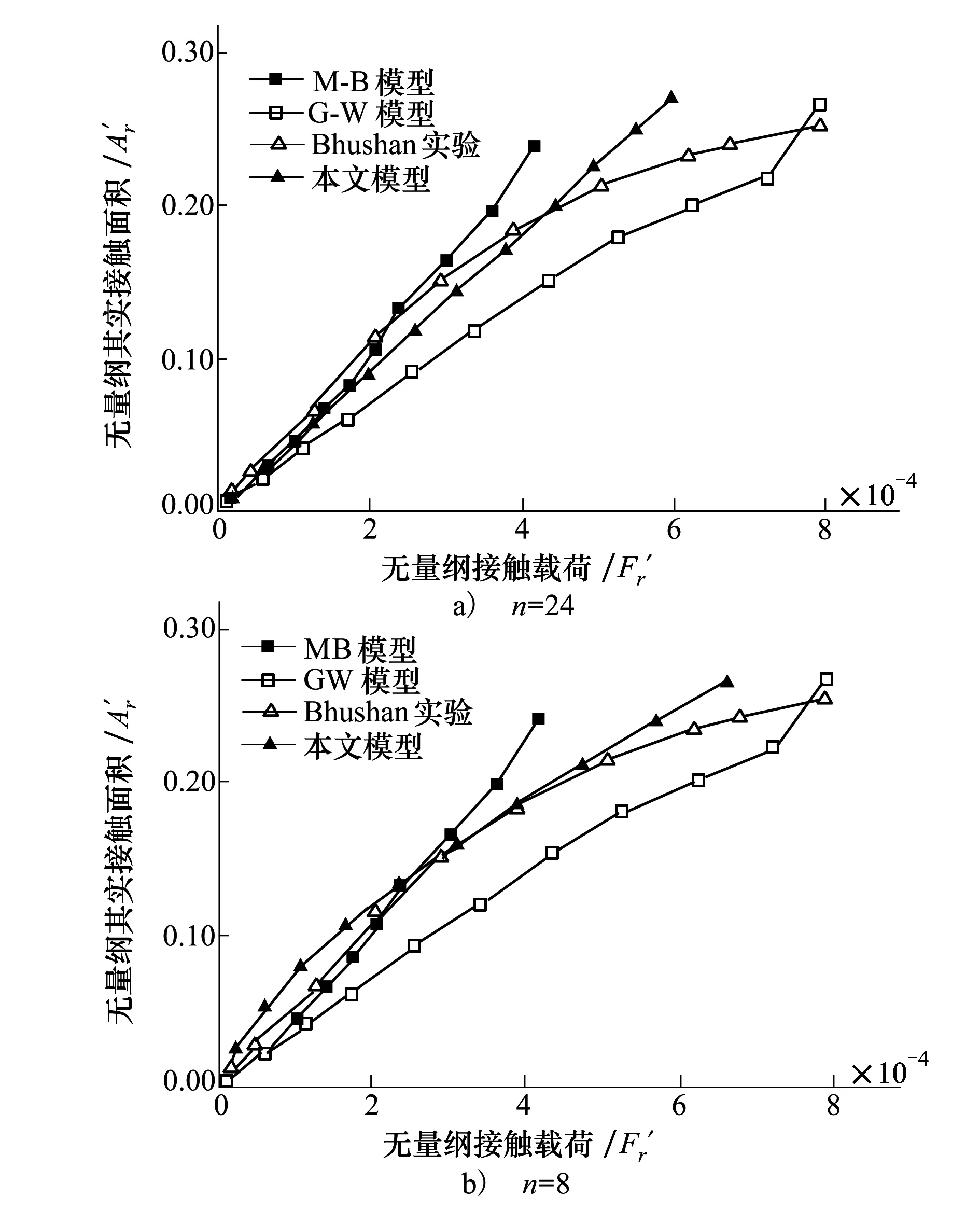
当an≤anec,所有微凸都体处于弹性变形状态;当anec

2)、当微凸体处于不同变形状态时,分为以下3种情况:

(1) 当最大微凸体处于弹性变形状态时,其余微凸体可能处于第一弹塑性变形状态。以本文计算结果,真实接触面积为

(37)

(38)

(39)

(2) 当最大微凸体处于弹性变形状态时,其余微凸体可能处于第二弹塑性变形阶段。同理可得真实接触面积的比值为:

(3) 当最大微凸体处于弹性变形状态时,其余微凸体可能处于完全塑形变形阶段。同理可得真实接触面积的比值为

式中，η表示选取不同微凸体所得到的真实接触面积的比值,下标1表示微凸体发生弹性变形和第一弹塑性变形,下标2表示微凸体发生弹性变形、第一弹塑性变形和第二弹塑性变形,下标3表示微凸体发生弹性变形、第一弹塑性变形、第二弹塑性变形和完全塑性变形。

为了说明我们选择最大微凸体来计算真实接触面积和载荷的合理性。我们又选择了小一级和小两级的微凸体,计算了其真实接触面积的与最大微凸体真实接触面积的比值。

经过计算,选择最大微凸体相邻的微凸体得到的总的真实接触面积与最大微凸体所得的真实接触面积的比值都小于50%,为了获得准确的计算结果,可以用最大微凸体的临界接触面积来计算整个粗糙表面的真实接触面积和载荷。

经过误差分析,在微凸体下压量与微凸体高度比值相同的情况下,最大微凸体的接触面积是最大的,因而粗糙表面中最大微凸体的力学性能直接决定整个粗糙表面的力学性能。当最大微凸体发生弹性变形,即使较大等级的微凸体发生弹塑性变形,对其整个粗糙表面的真实接触面积的影响很小,从工程应用和保守计算角度分析,选取最大微凸体的临界接触面积计算整个粗糙表面的真实接触面积和接触载荷是合理的。

3数值仿真结果与分析

基于前文所推导出的计算结果,分析粗糙表面接触过程中的真实接触面积与微凸体总接触载荷之间的关系。粗糙表面相关参数为:轮廓分形维数D分别取1.5、1.7、1.9,轮廓特征尺度系数取G=2.5×10-16～2.5×10-7,泊松比ν=0.3,材料的弹性模量E=2.3×1011N/m2,硬度为H=6.58×108N/m2。

图2为微凸体的临界接触面积(弹性临界接触面积、第一弹塑性临界接触面积和第二弹塑性临界接触面积)与微凸体等级之间的关系。

图2　微凸体的临界接触面积与等级之间的关系

粗糙表面的分形参数为D=1.5,G=2.5×10-9。其中:Ⅰ为弹性变形区;Ⅱ为第一弹塑性变形区;Ⅲ为第二弹塑性变形区;Ⅳ为完全塑性变形区。在Ⅰ区域中,这些等级的微凸体只能发生弹性变形;在区域Ⅱ中,这些等级的微凸体可以发生弹性变形和第一弹塑性变形;在区域Ⅲ中,这些等级的微凸体可以发生弹性变形、第一弹塑性变形和第二弹塑性变形;在区域Ⅳ中,这些等级的微凸体可以发生弹性变形、弹塑性变形和完全塑性变形。从图2中可以看出,当表面的分形参数一定时,单个微凸体的临界接触面积aec,aepc,apc是变化的,是和微凸体的尺度相关的,随着微凸体的等级n的增大而减小。对于确定等级的微凸体,随着接触面积的增大,微凸体先发生弹性变形,再发生弹塑性变形,最后发生完全塑性变形。

图3为在轮廓的分形维数D=1.5的情况下,微凸体的临界等级(弹性临界等级、第一弹塑性临界等级和第二弹塑性临界等级)与轮廓的特征尺度参数之间的关系。由图3可知,3种临界等级都随着轮廓尺度参数的增大而减小。在相同的特征尺度参数下,第二弹塑性临界等级最大,弹性临界等级最小,而第一弹塑性临界等级介于这2种临界等级之间。当轮廓尺度参数G增大到一定值时,临界等级小于零,但事实上,最大微凸体的等级大于零的,因此当分形维数为D=1.5时,轮廓的特征尺度参数不能大于2.5×10-7m。

图3　微凸体的临界等级与轮廓特征尺度参数之间的关系

图4　　　　无量纲接触载荷与无量纲　　　真实接触面积之间的关系

4与其他模型的比较

图5　不同接触模型与实验对比

5结论

1) 分形粗糙表面中单个微凸体的临界接触面积aec,aepc,apc是和微凸体的尺度相关的,临界接触面积是由材料属性和微凸体等级n共同决定。在确定的材料属性条件下,单个微凸体临界弹性接触面积与微凸体等级成反比。

2) 材料属性和分形参数一定时,粗糙表面上的接触载荷与最大微凸体接触面积和其对应的临界弹性接触面积相关,实际计算时,只要得到分形粗糙表面上最大微凸体接触面积和其对应的弹性临界接触面积就可获得整个粗糙表面上的接触载荷与真实接触面积,避免对粗糙表面进行弹塑性及完全塑性的重复计算,简化计算步骤。

3) 粗糙表面接触过程中,最大微凸体所处的等级范围不同,粗糙表面表现出来的力学性能也不相同。在整个粗糙表面接触过程中,粗糙表面变形过程与单个微凸体的变形过程一致。接触面积一定时,轮廓分形维数增大,接触载荷减小。

参考文献：

[1]Greenwood J A, Williamson J B P. Contact of Nominally Flat Surfaces[J]. Mathematical and Physical Sciences, 1966, 295(1442): 300-319

[2]Chang W R, Etsion I, Bogy D B. An Elastic-Plastic Model for the Contact of Rough Surfaces[J]. ASME Journal of Tribology, 1987, 109: 257-263

[3]Majumdar A, Bhushan B. Fractal Model of Elastic-Plastic Contact between Rough Surfaces[J]. ASME Journal of Tribology, 1991, 113: 1-11

[4]Kogut L, Etsion I. Elastic-Plastic Contact Analysis of a Sphere and a Rigid Flat[J]. ASME Journal of Applied Mechanics, 2002, 69(5): 657-662

[5]Morag Y, Etsion I. Resolving the Contradiction of Asperities Plastic to Elastic Mode Transition in Current Contact Models of Fractal Rough Surfaces[J]. Wear, 2007, 262(5/6): 624-629

[6]Jeng Luen Liou, Chi Ming Tsai, Lin Jenfin. A Microcontact Model Developed for Sphere-and Cylinder-Based Fractal Bodies in Contact with a Rigid Flat Surface[J]. Wear, 2010, 268: 431-442

[7]Miao Xiaomei, Huang Xiaodiao. A Complete Contact Model of a Fractal Rough Surface[J]. Wear, 2014, 309: 146-151

[8]丁雪兴, 严如奇, 贾永磊. 基于基底长度的粗糙表面分形接触模型的构建与分析[J]. 摩擦学学报, 2014, 34(4): 341-347

Ding Xuexing, Yan Ruqi, Jia Yonglei. Construction and Analysis of Fractal Contact Mechanics Model for Rough Surface Based on Base Length[J]. Tribology, 2014, 34(4): 341-347 (in Chinese)

[9]Johnson K L. Contact Mechanics[M]. London: Cambridge University Press, 1985: 79-128

[10] Wang S, Komvopoulos K. A Fractal Theory of the Interfacial Temperature Distribution in the Slow Sliding Regime: PartⅡ——Multiple Domains, Elastoplastic Contacts and Applications[J]. ASME Journal of Tribology, 1994, 116(4): 824-832

[11] Bhushan B. The Real Area of Contact in Polymeric Magnetic Media-PartⅡ: Experimental Data Analysis[J]. ASLE Transactions, 1985, 28: 181-197

收稿日期：2015-10-27

基金项目：国家自然科学基金(51105304、51475364)与陕西省自然科学基础研究计划(2015JM5212)资助

作者简介：成雨(1991—)，西安理工大学硕士研究生，主要从事接触、摩擦理论方法研究。

中图分类号：TH117

文献标志码：A

文章编号:1000-2758(2016)03-0485-08

The Elastic-Plastic Contact Mechanics Model Related Scale of Rough Surface

Cheng Yu1, Yuan Yuan1, Gan Li1, Xu Yingqiang2, Li Wanzhong2

1.School of Mechanical and Precision Instrument Engineering, Xi′an University of Technology, Xi′an 710048, China 2.School of Mechanical Engineering, Northwestern Polytechnical University, Xi′an 710072, China

Abstract:The real contact state between the rough surfaces is studied with fractal theory, a fractal contact mechanics model for rough surfaces is proposed also. Considering the asperity level, the expressions among elastic critical level, the first elastic-plastic critical level and the second elastic-plastic critical level are obtained. The conditions existence of elastic deformation, elastic-plastic deformation and fully plastic deformation of each level asperity are researched on the rough surface, the expressions among the critical contact area in the three regimes are derived respectively. Considering the asperity size distribution function, the analytic expression between the total contact load with the real contact area is obtained. Calculation results show that the critical contact areas of a single asperity are related to its scale, and its reduce while the level of asperity increases. As the load and contact area increase a transition from elastic, elastic-plastic to fully plastic contact model takes place in this order and agreed with classical contact mechanics. During the whole rough surfaces contact, the deformation process of the rough surfaces is consistent with a single asperity. The largest asperity is in different critical levels, mechanical properties of the rough surface are not the same.

Keywords:rough surfaces; asperity; fractal dimension; scale; critical contact area; elastic-plastic contact; density function; two dimensional; topology; models analysis; mechanical properties; deformation; friction