水平井钻柱系统动力学特性分析模型的建立*

吴泽兵 张文溪 袁若飞 沈 飞 刘家乐 贺啸林

(西安石油大学机械工程学院)

0 引 言

随着石油钻井技术的应用日益广泛，钻柱失效问题也日益突出。因此，钻井工程中急需了解钻柱在井下的运动状态，以进行钻柱的动力学特性方面的研究[1-2]。水平井是从垂直井段转变为水平井段，钻井施工难度较大。钻柱具有很大的长细比，其动力学特性的研究十分困难[3-4]。

钻具组合优化、钻井参数优选等一系列问题可通过钻柱动力学来解决[5]。美国Tulsa大学的M.W.DYKSTRA[6]借鉴其他领域中解决转子动力学问题的方法来研究钻柱并完成了“非线性钻柱动力学”。毛良杰等[7]基于钻柱动力学原理分析了底部钻具组合的疲劳寿命。吴泽兵等[8]基于ADAMS软件，建立水平井全井钻柱-井壁动态非线性接触模型，分析了水平井钻柱接触力分布情况。石明顺[9]基于钻井钻柱非线性动力学模型对定向钻井中钻柱-井壁系统进行非线性动力学仿真分析。ZHU X.H.等[10]基于考虑了轴向、横向和扭转振动的有限元模型，通过改变井身结构和底部钻具组合等，探讨了钻柱系统振动特性差异较大的原因。N.K.TENGESDAL等[11]基于拉格朗日方法，提出了一种考虑侧向弯曲、纵向运动和扭转变形的钻柱动态模型。冯群芳等[12]采用拉格朗日方程建立了斜井下钻柱横-扭耦合非线性动力学模型，总结了钻柱与井壁接触、钻柱扭矩耗散和井眼轨迹等因素对钻柱系统动力学特性的影响规律。朱杰然等[13]分析了无钻压加载条件下的水平井钻柱系统在不同井段和不同钻井工况参数下的动力学响应。亓传宇等[14]分析并总结了钻井深度对煤矿水平井钻柱水平段振动特性的影响规律。

前期钻柱系统动力学特性分析大多数是对直井或斜井内水平段或造斜段部分钻柱进行研究，分析时假定钻柱已钻进某一特定深度而并未考虑整个钻进过程。为此，笔者建立水平井钻柱仿真模型，模拟钻进全过程，揭示了钻柱的整体动力学特性，讨论了稳定器、大钩载荷以及卡钻情况对钻柱动力学特性的影响，以期更好地了解井筒内钻柱的实际运动状态，为钻柱研究设计及结构优化提供参考。

1 钻柱动力学模型

1.1 坐标系及坐标变换

水平井井眼轴线的形态是一条曲率不定的空间螺旋线[15]。在钻井过程中，假设井眼轴线与钻柱尚未变形时的轴线重合，为了便于描述钻柱的受力变形和井眼的形体，引用了整体坐标系和局部坐标系[16]。在整体坐标系中，地理北向为X轴的正向，地理东向为Y轴的正向，而Z轴的正向则是由井口指向井底，井口处设置坐标原点。局部坐标系中钻柱的轴线为x轴，其正向为钻柱轴向进给方向；y轴垂直于x轴并指向靠近地面方向，由右手坐标系的规则来确定。

以整体坐标系X轴为旋转轴，顺时针旋转α角，就可以从原来的坐标系OXYZ转变为用来描述钻柱单元的局部坐标系Ox1y1z1，如图2a所示。具体的转换公式为：

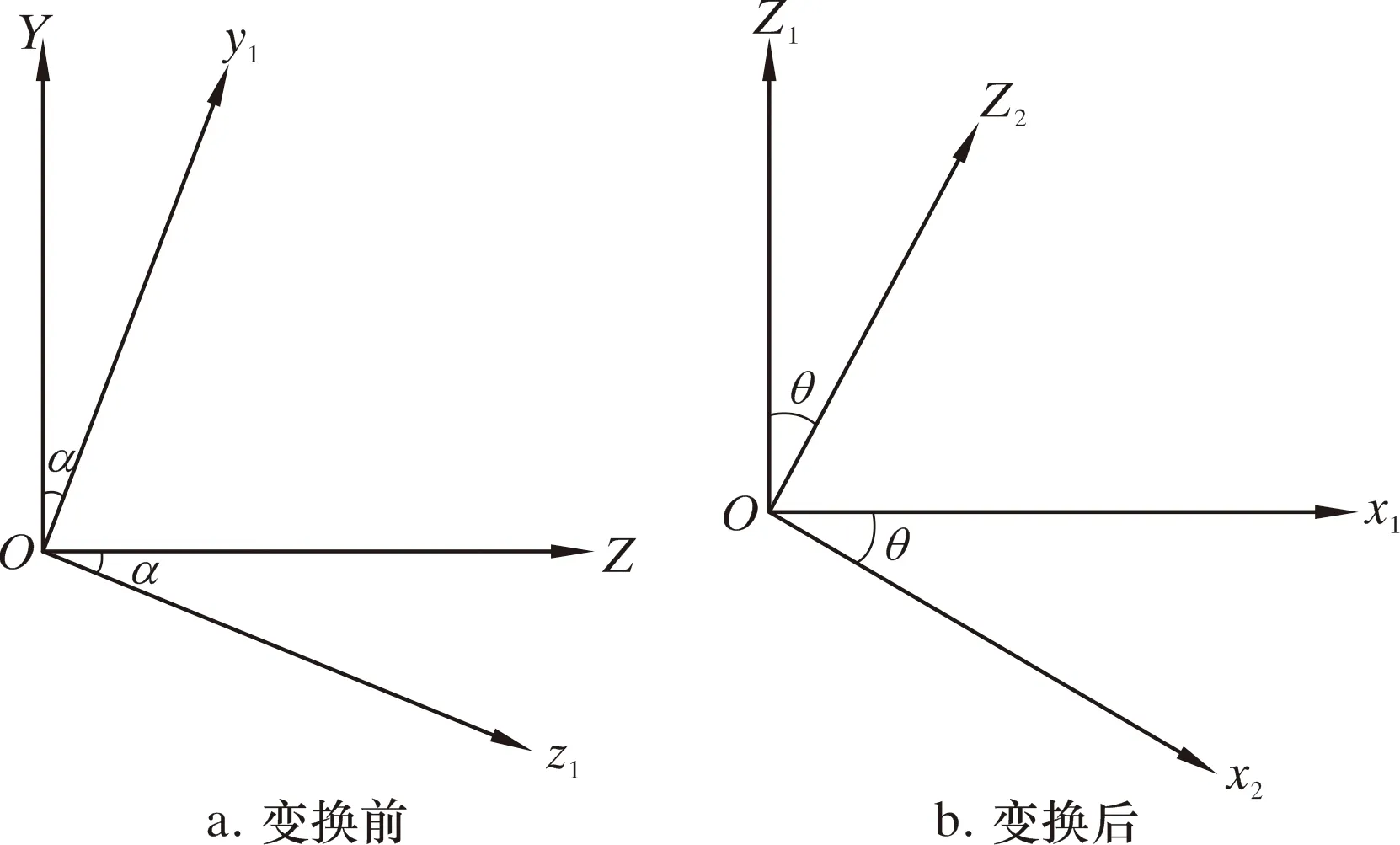
图2 坐标转换示意图Fig.2 Schematic diagram of coordinate conversion

(1)

然后再绕转换后的局部坐标系y1顺时针转θ角，从Ox1y1z1坐标系转换为用来描述钻柱单元的局部坐标系Ox2y2z2，如图2b所示。其表达式为：

(2)

结合式(1)和式(2)，整体坐标系转换2次后，转变为描述钻柱单元的局部坐标系，具体转换关系式为：

(3)

1.2 动力学模型

钻柱单元位移和节点力如图3所示。

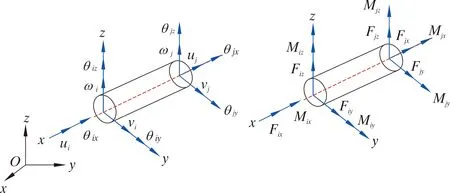
图3 钻柱单元节点位移和节点力示图Fig.3 Schematic diagram for nodal displacement and nodal force of drill string unit

在局部坐标系下，任一钻柱单元在t时刻的节点广义位移、广义速度和广义加速度向量表达式分别为：

de(t)=[ui(t)，vi(t)，wi(t)，θix(t)，θiy(t)，θiz(t)，uj(t)，vj(t)，wj(t)，θjx(t)，θjy(t)，θjz(t)]

(4)

(5)

(6)

钻柱单元广义位移、广义速度和广义加速度公式分别为：

f(t)=Nde(t)

(7)

(8)

(9)

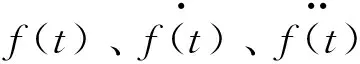
(10)

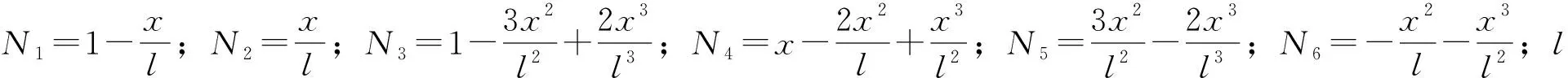
钻柱单元的几何方程和物理方程分别为：

(11)

σ(t)=Dε(t)-Dε0+σ0

(12)

式中：BNL、BL为应变矩阵；D为弹性矩阵，Pa；ε0为钻柱单元初应变；ε(t)为t时刻单元应变；σ(t)为t时刻单元应力，Pa；σ0为钻柱单元初始应力，Pa。

基于多自由度系统的Lagrange方程推导钻柱单元运动方程为：

(13)

(14)

(15)

(16)

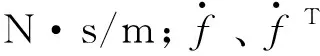
将式(14)、式(15)、式(16)代入式(13)，化简后得到钻柱单元动力学方程：

(17)

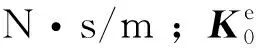
由单元动力学方程得到钻柱系统动力学方程为：

(18)

1.3 边界条件

(1)上边界条件。井口边界是地基边界则为固定位移边界。在扭转方向上，井口为已知扭转角位移、角速度和角加速度边界。

(2)下边界条件。钻头破岩时做轴向移动和旋转运动，钻压和扭矩同时作用于钻头上，将井底钻头处的横向线位移固定、角位移自由、扭转角位移为已知力边界。

(3)钻柱与井壁碰撞接触边界。钻柱与井壁的碰撞接触沿井深和井眼圆周方向呈多点、多方位的随机分布。钻柱与井壁的碰撞模型如图4所示。

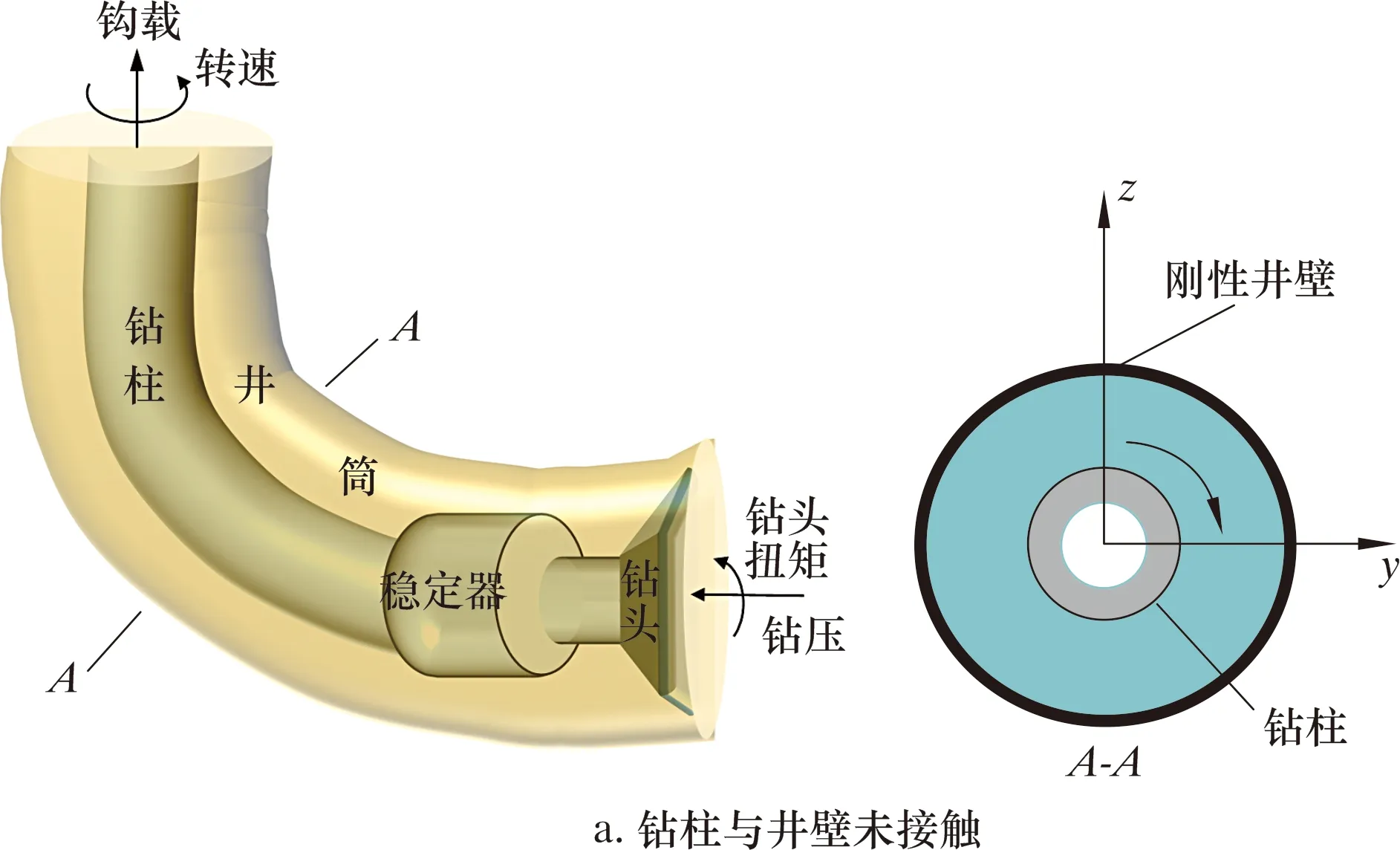
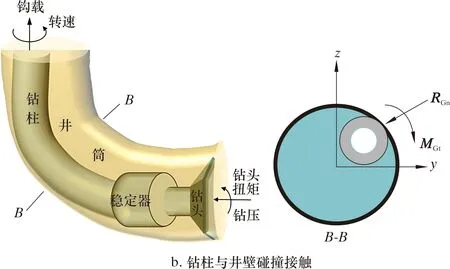
图4 钻柱与井壁碰撞模型Fig.4 Collision model of drill string and borehole wall

钻柱与井壁碰撞接触产生碰撞反力RGn的同时还会产生附加力矩，为：

(19)

式中：RGt为切向摩阻力，N；RGA为轴向摩阻力，N；μ1为静摩擦因数；μ2为动摩擦因数；MGt、MGA分别为扭矩和弯矩，N·m。

1.4 Johancsik模型

Johancsik模型是Johancsik提出的一种从钻柱底部开始计算，逐步向上进行的一种计算钻柱阻力和轴向力的模型。Johancsik提出钻柱的每一个短单元都对总运行载荷的轴向和扭转载荷有较小的增量[17]，从钻柱底部单元开始迭代计算即可推算出每个单元的轴向载荷及顶部单元大钩载荷的值。图5a和图5b分别说明了钻柱单元受力及钻柱钻进时作用在钻柱元件上的力。

图5 钻柱单元受力分析Fig.5 Force analysis of drill string unit

其中，法向力Fn是重力W和2个拉力Ft、Ft+ΔFt的法向分量的负矢量和，表达式为：

(20)

由Fn的方程式可得到ΔFt的方程式：

(21)

2 钻柱动力学仿真模型建立

2.1 基本假设

(1)忽略钻柱螺纹连接处、局部孔和槽等位置的刚度；

(2)保持井眼直径及曲率不变，其横截面始终为圆形；

(3)钻柱视为均质圆环截面弹性梁单元组成，钻柱变形处于线弹性；

(4)不考虑钻井液的影响；

(5)钻柱钻进前，其轴线与井眼轴线重合，钻头与井筒之间无间隙。

2.2 三维仿真模型建立

利用SolidWorks软件建立钻柱单元模型、扶正器、ø311 mm钻头以及井壁模型，并完成水平井钻柱模型装配。各部件的具体尺寸为：钻柱外径127.0 mm，内径76.0 mm，总长480.0 mm，密度7 801 kg/m3，弹性模量207 GPa；井筒外径400.0 mm，内径315.0 mm，竖直井段长100 m，弯曲段曲率半径180 m，水平段长100 m；钻头最大外径311.0 mm。

2.3 钻柱单元柔性化及动力学仿真模型建立

为了使仿真模拟更加贴近实际情况，将三维模型导入ADAMS软件后设置钻柱单元材料为刚体，单元与单元之间固定连接，钻柱单元逐个采用ADAMS软件柔性化模块直接柔性化。其他零部件如井筒、钻头、扶正器等的材料设置成刚体，井筒与大地为固定副，形成刚柔耦合的动力学仿真模型，如图6所示。

2.4 约束条件和接触关系

井口钻柱受大钩载荷和转盘约束影响，只能沿轴向运动和绕轴转动，剩余自由度全部约束。钻头破岩时做轴向移动和旋转运动，其横向位移受到约束，此外还受钻头与地层的相互作用产生的激振力和扭矩的作用[18]。

ADAMS提供了3种接触力的计算方法，分别是Restitution、Impact和User Defined。其中，Impact是基于碰撞函数的接触算法，由于井壁和钻柱是随机碰撞接触，所以接触力选用Impact方法求解。参数设置：刚度K为35 000，阻尼c为28，指数为1.5，透深为0.1，静摩擦因数为0.05，动摩擦因数为0.03。

2.5 模型验证

为确保仿真结果的可靠性，用Johancsik模型与笔者建立的水平井钻柱系统钻进仿真模型计算钻柱钻进时产生的轴向力，2种计算结果对比如图7所示。

图7 Johancsik模型与ADAMS模型结果对比Fig.7 Comparison of results from Johancsik and ADAMS models

从图7可以看到，2种模型得到的轴向力变化趋势基本一致，进一步验证了仿真模型的正确性。

3 动力学特性分析

3.1 稳定器对钻柱动力学特性的影响

3.1.1 稳定器对钻柱接触力的影响

在建立的钻柱刚柔耦合仿真模型上添加稳定器来分析稳定器对钻柱动力学特性的影响，仿真结果如图8所示，其中红色箭头为钻柱与井筒的接触力。

图8 水平井钻柱模型钻进仿真结果Fig.8 Drilling simulation results of drill string model of horizontal well

图9为有、无稳定器钻头处接触力随时间变化曲线对比。从图9可以看出，钻柱加稳定器后，钻头与井壁的接触力幅值变化明显小于未加稳定器的情况。这个现象说明，钻柱加稳定器后减少了钻柱与井壁的碰撞，使得钻柱与井壁的接触次数减少，随之产生的接触力也相对较小。

图9 有、无稳定器钻头处接触力随时间变化曲线对比Fig.9 Variation of contact force over time at bit with and without stabilizers

3.1.2 稳定器对钻柱横向振动特性的影响

图10展示了钻柱在钻进过程中有、无稳定器对钻头处横向位移、速度、加速度的影响。从图10可以发现，加稳定器后钻头处的横向位移、速度、加速度均减小，即钻头处的横向振动减弱，这进一步验证了前文所述的加稳定器后钻柱与井壁的接触频率降低这一结论的正确性。

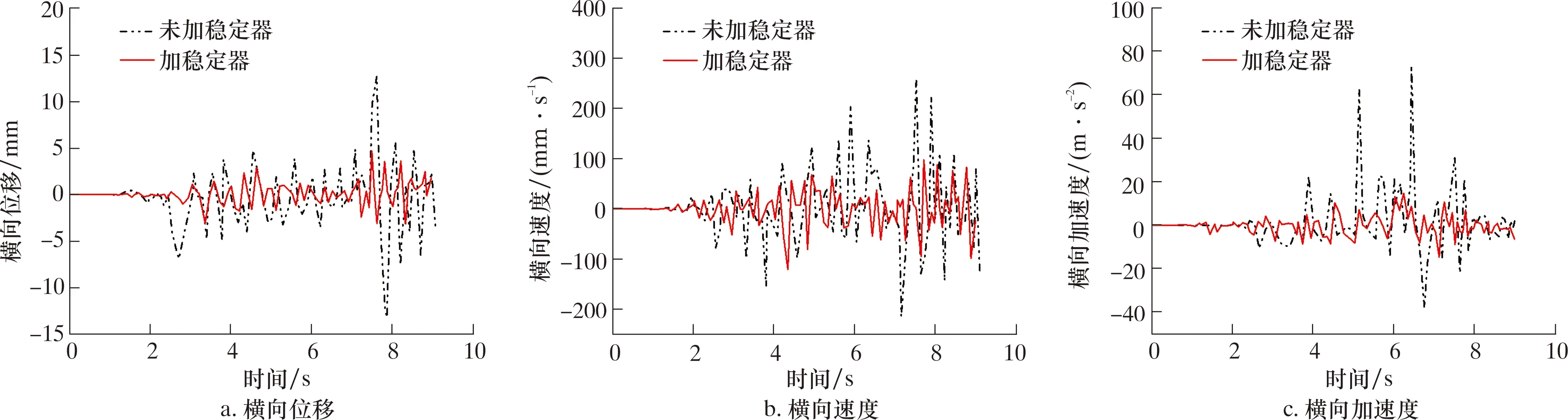
图10 有、无稳定器钻头处横向振动特性对比曲线Fig.10 Lateral vibration characteristics at bit with and without stabilizers

3.2 卡钻对钻柱屈曲特性的影响

3.2.1 卡钻对水平段钻柱屈曲特性的影响

为分析卡钻对钻柱屈曲特性的影响，模拟卡钻的情况对钻柱进行屈曲特性仿真分析。将钻柱-钻头-井壁模型简化为钻柱-井壁模型，以便于仿真计算分析。在水平井钻柱钻进的过程中，钻头发生卡钻时，钻柱水平段不同时刻的屈曲特性如图11所示。

从图11可以清楚看到，在重力的作用及钻柱底部卡钻的影响下，井眼内的钻柱水平段形态随时间的变化而发生变化。从0.6～2.4 s钻柱的截面角位移大于30°，钻柱的屈曲变形为螺旋屈曲；从2.4～3.6 s钻柱产生截面小于30°的角位移，钻柱的屈曲变形为正弦屈曲。

由此分析可得，钻柱随着时间的延续，钻柱屈曲特性逐步从螺旋屈曲转变为正弦屈曲。图11的红色线箭头展示了在不同时刻水平段钻柱与井壁的接触力。从图11可以直观地看到钻柱与井壁的接触力的数量也在随时间的延续而增加。

3.2.2 卡钻对竖直段钻柱屈曲特性的影响

图12为钻头卡钻情况发生时钻柱竖直段不同时刻的屈曲特性。

由图12可知，与钻柱水平段情况相似，在钻柱自重及底部卡钻双重影响下，井眼内的钻柱竖直段形态随时间的变化而变化，钻柱与井壁的接触碰撞也发生相应的变化。0.4～1.6 s井筒内的下半段钻柱与井筒外上半段钻柱均出现螺旋屈曲现象；1.6～2.8 s井筒内的下半段钻柱发生正弦屈曲变形，井筒外上半段钻柱依旧发生螺旋屈曲变形；2.8～3.6 s钻柱整体变形为正弦屈曲。归纳可得，竖直段钻柱变形规律为随着时间的延续钻柱由螺旋屈曲向正弦屈曲转化。

3.3 大钩载荷对钻柱动力学特性的影响

3.3.1 大钩载荷对钻柱接触力的影响

图13描述了有、无大钩载荷时钻头处接触力随时间变化的情况。从图13可直观地发现，加大钩载荷后井壁与钻柱的接触力明显减小，这种情况说明大钩载荷有利于减少钻柱与井壁的碰撞以及钻柱失效情况的发生，进一步说明研究大钩载荷对钻柱动力学特性的影响十分必要。

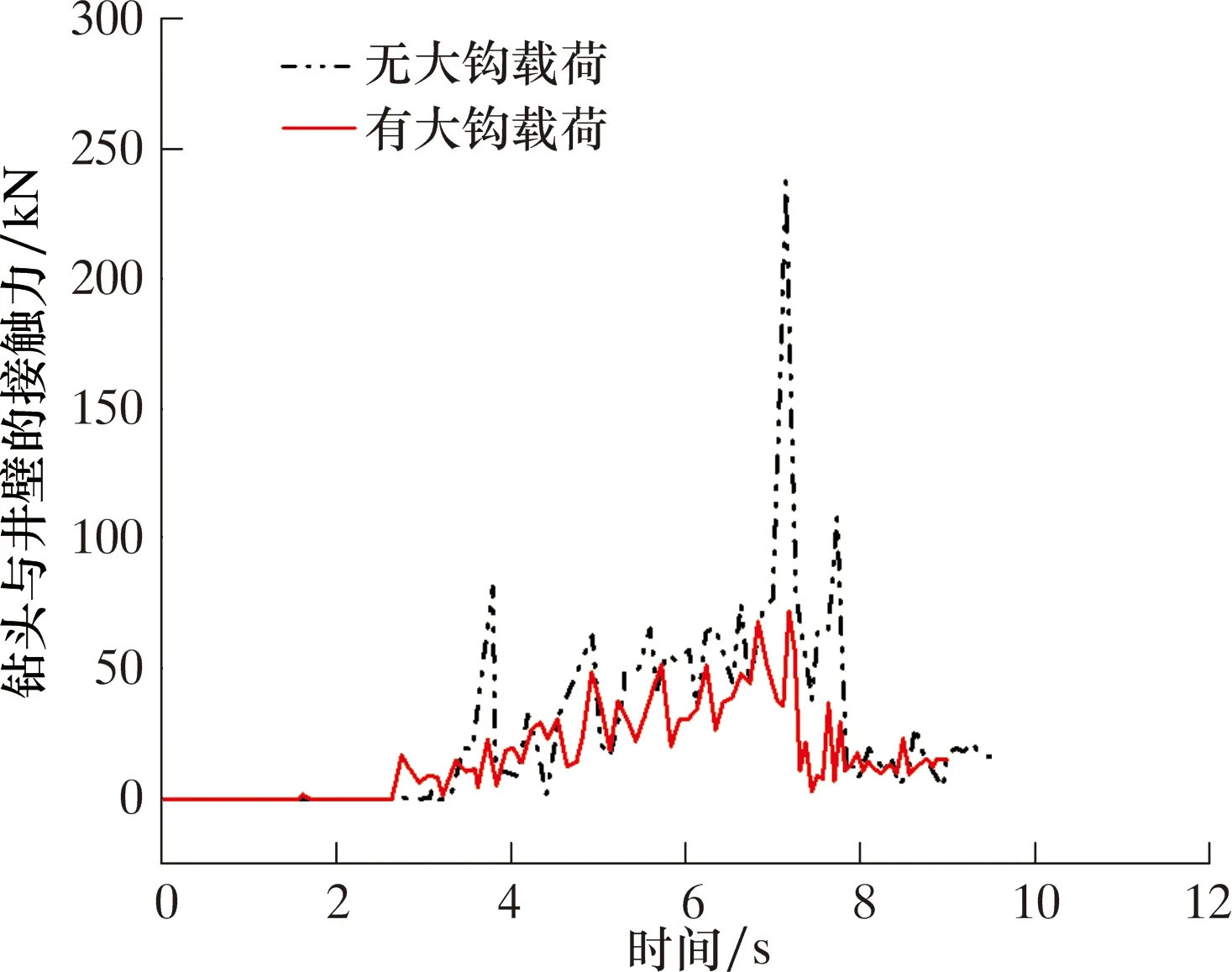
图13 有、无大钩载荷钻头处接触力随时间变化曲线对比Fig.13 Variation of contact force over time at bit with and without hook loads

为讨论大钩载荷对钻柱动力学特性的影响且考虑所建钻柱模型重力为311.726 kN，笔者对钻柱模型分别施加240、250、260及270 kN的大钩载荷。经仿真分析发现，当施加270 kN的大钩载荷时，钻柱在钻进过程中会发生停止钻进的情况。确定在钻柱顶端可施加的临界大钩载荷为260 kN左右。这说明在实际作业中，在钻头处施加大钩载荷时，应先模拟计算得到临界大钩载荷值，且应根据实时工况随时调整大钩载荷数值。

3.3.2 大钩载荷对钻柱轴向进给特性的影响

大钩载荷对钻头处进给速度及进给加速度的影响如图14所示。由图14可得，在钻柱施加大钩载荷后钻柱的进给速度增长明显减缓，钻柱的进给加速度的幅值变化也明显降低。其中当施加的大钩载荷小于等于临界值时，大钩载荷数值越大钻柱的进给速度及加速度便越小。结果表明，施加大钩载荷后会降低钻柱的钻进速度，减少底部岩石对钻头的破坏，对钻柱有一定的保护作用，亦可通过调节大钩载荷来控制钻柱的钻进速度。

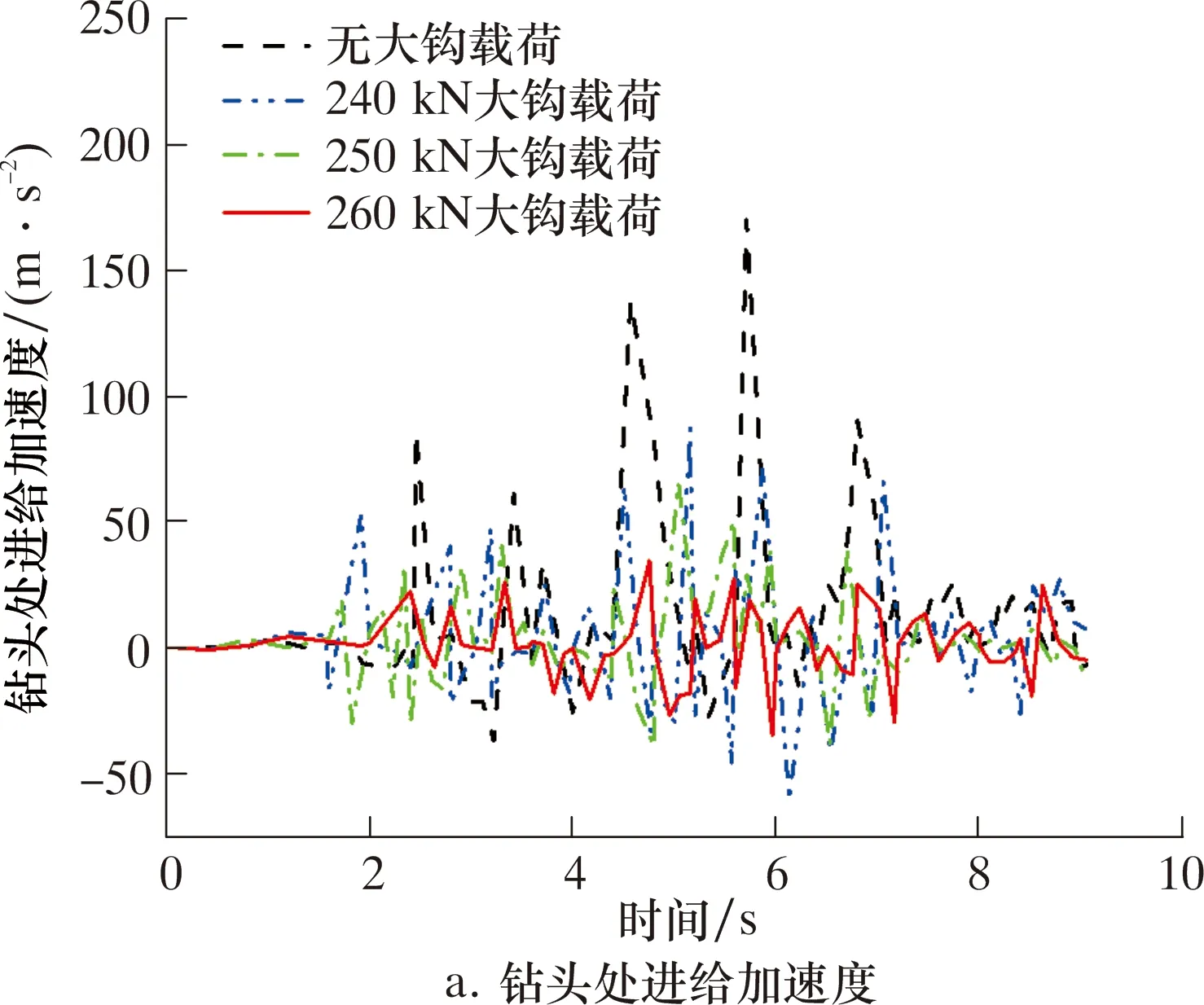
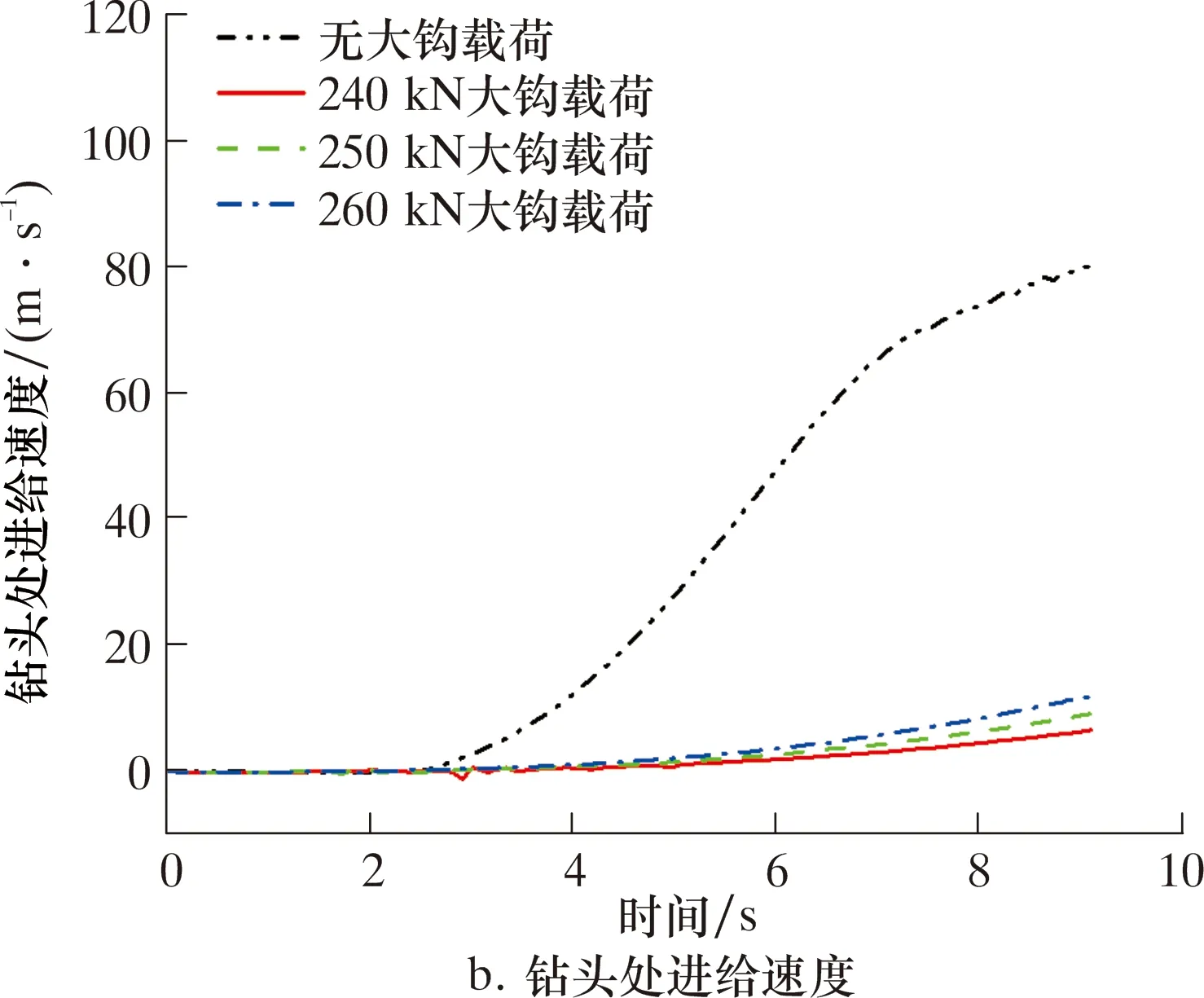
图14 不同大钩载荷时钻柱轴向进给特性Fig.14 Axial feed characteristics of drill string under different hook loads

3.3.3 大钩载荷对钻柱横向振动特性的影响

图15给出了不同大钩载荷钻头处横向振动特性对比曲线。

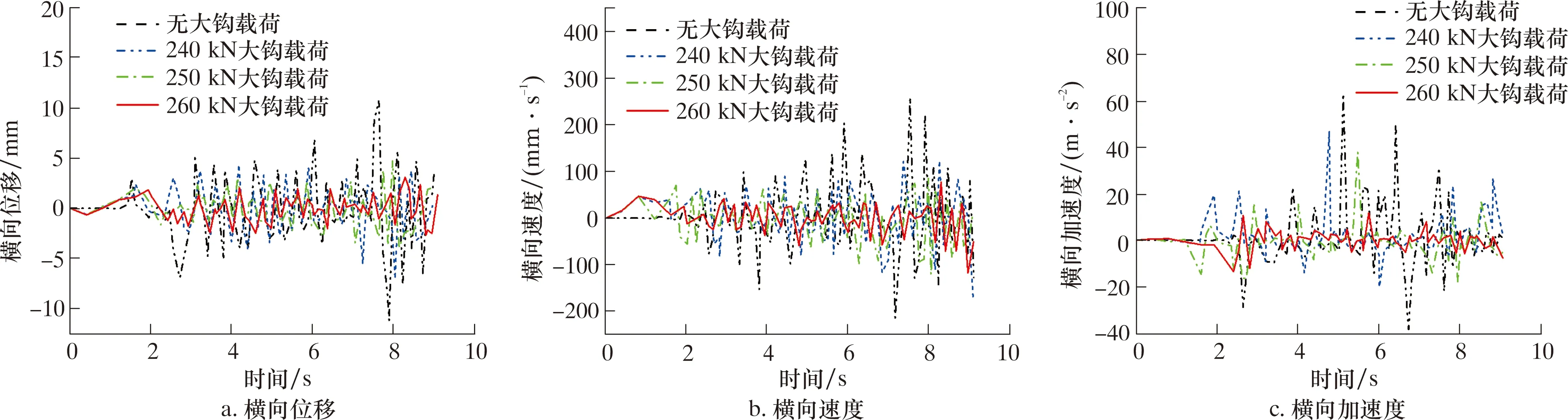
图15 不同大钩载荷时钻头处横向振动特性Fig.15 Lateral vibration characteristics at bit under different hook loads

从图15可以看到，加大钩载荷后钻头处的横向位移、速度及加速度明显小于未加大钩载荷时，且这3个变量随大钩载荷的增加而减少。这种情况说明钻柱顶部的大钩载荷减少了钻柱的横向振动，恰恰验证了前文所述的施加大钩载荷后降低了钻柱与井壁碰撞频率的正确性，以及当大钩载荷值小于临界载荷时，大钩载荷的值越大钻柱横向振动越稳定，与井壁碰撞频率越低。

4 结论及认识

(1)模拟水平井钻柱系统钻进全程，验证了钻柱加稳定器后可减小钻柱与井壁的碰撞频率，使得钻柱与井壁的接触减少，随之产生的接触力及横向振动也相对较小。

(2)模拟钻头发生卡钻的情况，水平段钻柱随着时间的延续，钻柱屈曲特性逐步从螺旋屈曲转变为正弦屈曲；竖直段钻柱变形规律类似，即随着时间的延续，钻柱由螺旋屈曲向正弦屈曲转化。

(3)经模拟分析确定临界大钩载荷值为260 kN，当在钻柱端施加的大钩载荷大于临界值时，钻柱在钻进过程中会发生卡钻的情况；当施加的大钩载荷小于临界值时，大钩载荷的值越大，钻柱横向振动越稳定，与井壁碰撞频率越低，钻柱与井壁的接触力也就越小。

(4)未考虑钻井液、槽的刚度等复杂条件对水平井钻柱系统的影响，则模拟结果具有一定的局限性，因此在对钻柱系统动力学特性分析及优化时，应考虑这些复杂条件。