基于改进贝叶斯算法的黏滑振动等级评估研究*

邓杨林 李玉梅 张 涛 郭 鹤 石广远 陈学勇

(1.北京信息科技大学高动态导航技术北京市重点实验室 2.现代测控技术教育部重点实验室 3.中国石油天然气股份有限公司华北油田公司第三采油厂)

0 引 言

钻柱振动是限制钻井性能的频繁且持久的因素。钻柱振动可分为轴向振动(垂直)、横向振动(旋转)和扭转振动(黏滑)。据统计，每年40%的钻井深度会受到钻井振动的影响[1-3]。例如轴向振动时钻头反弹、横向振动时向前或向后旋转、扭转振动时会黏滑。严重的黏滑振动可能会导致井下工具的潜在损坏，轻微的黏滑振动会显著减慢钻井进度[4]。国内外学者对井下振动的研究越来越多，这对钻井技术研究具有重要的工程价值。

振动建模和监测是一个复杂的过程，需要理想的条件，但是在实际钻井过程中，这些理想条件不能适用于不同的BHA(井底钻具组合)、油藏、地质和地层[5-6]。随着井下测量工具技术的发展，利用井下钻井数据，使用数据驱动模型来监测钻柱变得可取。C.HEGDE等[7]提出了一种利用钻井作业参数对基于振动的度量进行分类的新方法——黏滑指数(ISS)，然后使用机器学习算法对ISS的严重程度进行分类。该模型可与ROP优化模型结合使用，在提高ROP的同时控制钻井振动。T. BAUMGARTNER等[8]建立了一个简单的动力学模型，研究了旋转和黏滑振动情况下的高频加速度测量输出，并使用基于贝叶斯分类算法，从高频振动数据中提取和分析特征以进行黏滑振动识别。唐翰文等[9-12]针对近钻头黏滑数据时频域分析，提取主要特征向量，建立了基于优化XGBoost的黏滑振动等级识别分类模型。陈冲等[13]为评估钻柱黏滑振动的严重程度，提出了一种基于因子分析(FA)与支持向量机(SVM)的黏滑振动风险评估方法。受限于高精尖井下随钻测量工具以及测量参数的影响，目前关于黏滑振动分析大多数基于地面数据进行。虽然地面测量通常以1～10 Hz的频率采样，但是它们通常以0.2～1.0 Hz比较低的速率存储和传输，导致大多数井下功能障碍无法被发现和检测[14]。

本文针对黏滑振动严重等级评估问题，提出了一种DE＿AWNB(基于差分演化算法的加权朴素贝叶斯分类算法)改进模型。主要是通过采用新型井下近钻头多功能参数高频测量短节，采集井下振动数据。并将属性加权朴素贝叶斯法和差分演化算法相结合，在DE-AWNB中，每个属性都会随机分配到一个权重，利用DE算法进行权重寻优，迭代得到最优权重组合。通过将高频振动数据与该算法的结合，可有效解决上述问题。

1 黏滑振动分级原理

黏滑是一种旋转速度周期性变化的扭转振动。在黏滑严重的情况下，钻头可能完全停止，然后速度上升到原来的几倍，然后减速，再停止旋转。造成黏滑的原因是，管柱的扭转强度过低，无法克服切削齿与地层、稳定器与井壁之间的摩擦力。在黏滞循环期间，尽管地面输入恒定的转速，钻头依然会停止旋转，然后钻柱向上弯曲，直至施加到足够的扭转力来克服摩擦力，从而形成滑移循环[15]。通过在井下使用加速度计测量振动，3个加速度计沿工具中轴线以相互正交的方式安装，X轴传感器测量轴向冲击，Y和Z轴传感器测量正交方向上的横向冲击。黏滑是一种明显的低频现象，其周期从1～10 s不等。三轴加速度计测得的加速度会有周期性和间接性波动。

图1是新疆油田某井段发生严重黏滑时实测到的三轴加速度数据。

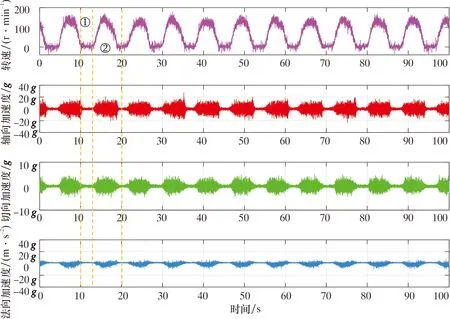
图1 严重黏滑时转速、加速度变化曲线Fig.1 ROP and acceleration variation curves at the time of severe stick slip

图1中g为重力加速度，m/s2。图1所示黏滑周期约为9 s，在转速上升时，典型的旋转模式出现。位置②这个过程为滑脱阶段，持续时间约为6 s；且达到一定速度时，波动幅度较低，并在低转速的滑移循环结束时再次增加。位置①这个过程为黏滞阶段，持续时间约为3 s，同时发现三轴加速度带有同步的周期波动，且通过对比可以发现，黏滑过程中径向加速度远高于切向加速度，这种情况在整个黏滑振动中都有发生。图2显示的是正常钻进时的转速、三轴加速度曲线。与图1相比较，图2中的转速、三轴加速度没有出现周期性波动，且转速、三轴加速度的幅值较小。

图2 正常钻进时转速、加速度变化曲线Fig.2 ROP and acceleration variation curves in normal drilling

评价扭转振动对钻柱影响的常用指标是黏滑指数(ISS)[15-16]，该指数可以使用井下测量工程参数和地面参数计算。

(1)

式中：ωmax、ωmin和ωavg分别为钻头最大、最小及平均转速，r/min。

其中，钻头最大、最小转速可根据实测数据得出，平均转速为井场提供的地面平均转盘转速。在本次试验中，钻头平均转速取75 r/min。当ISS<1时，表明钻头总是向右转动，而在ISS=1时，达到完全黏滑的条件，钻头周期性停止转动片刻。ISS值越高，钻头停止转动的卡滞时间越长。E.W.ROBNETT等[17]利用转速的变化来确定黏滑的发生率和严重程度，黏滑振动划分为4个等级，如表1所示。

表1 黏滑振动等级标准Table1 Standards of stick-slip vibration grade

根据上述黏滑振动分级原理，对实测数据进行ISS计算，结果如图3所示。通过手动标签之后，就可以通过机器学习算法进行黏滑振动等级评估。

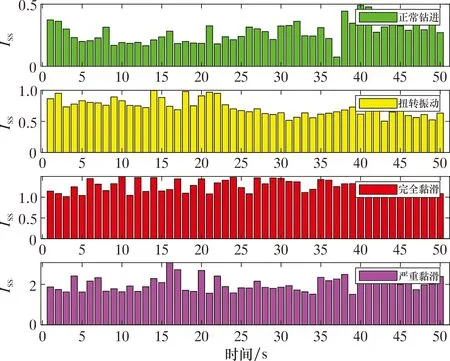
图3 ISS指标图Fig.3 ISS indicator chart

2 算法原理

2.1 朴素贝叶斯算法

朴素贝叶斯算法是一种以贝叶斯算法为基础，基于概率的分类算法。朴素贝叶斯算法假设各个特征之间相互独立，即一个特征的取值不会影响另一个特征的取值。假设一个数据集X={x1，x2，…，xn}，且每个样本中都包含n维特征，即x={a1，a2，…，an}。假定有m个种类，分别用C1，C2，…，Cm表示，根据贝叶斯定理，可得到x属于Cm类别的概率为：

(2)

式中：P(Ci)为属于类别Ci的概率；Ci为x的所属类别；P(Ci|x)为在x发生的条件下属于Ci类别的概率，被称为后验概率；P(x)为事件x的先验概率。

由于各个维度的特征属性相互独立，在此条件上，条件概率可以转化为：

(3)

式中：P(ak|Ci)为类别Ci中包含特征ak的概率。

于是，朴素贝叶斯分类器可表示为：

(4)

式中：P(C)为C类发生的概率；ak为第k个属性的值。

2.2 属性加权朴素贝叶斯算法

传统的朴素贝叶斯分类器的前提是各个特征之间相互独立，即条件独立性假设。然而现实中，事件与事件之间或多或少存在一定的关联性，对属性之间关联性强的来说，朴素贝叶斯分类的效果会受到巨大的影响。

属性加权针对每个属性对不同类别的影响程度不同，赋予每个属性不同的权重，改变每个属性的条件概率，缓解条件独立假设带来的影响，以此来提高分类准确率。对于给定的数据x={a1，a2，…，an}，可以用下面的公式来预测其类别：

(5)

式中：wi代表类属性的权重，且权重范围为[0，1]；c为所属于的类别。

2.3 差分演化算法

差分演化算法(Differential Evolution Algorithm，DE)是一种基于群体的启发式搜索优化算法。它的基本思想是通过以群体演化为基础，经过个体与个体之间的“自然选择”，经过多次迭代从而形成群体，使群体繁衍出更优的群体，从而收敛到最优解。基本操作流程包括：初始化、变异、交叉、选择。

初始化：建立一个初始种群，由NP个个体组成，每个个体都有D维向量可表示解决问题的个体参数，以及一个个体的适应度值。

i=1，2，…，NP；j=1，2，…，D}

(6)

式中：Xi(0)是第i个个体；j表示第j维。

(7)

变异：对新一代的个体进行变异操作，以提高个体的多样性，从而增强搜索能力，以期达到最优解。

Vi(g+1)=Xr1(g)+F(Xr2(g)-Xr3(g))

(8)

式中：r1、r2和r3是3个随机数，区间为[1，NP]；F称为缩放因子，是一个常数；g表示第g代。

交叉：根据每个个体的适应度值，选择出适应度较高的个体，并进行交叉操作，生成新一代个体。

(9)

式中：CR为交叉概率，通过概率的方式随机产生新的个体。

选择：从种群中选择出某些满足一定条件的个体，从而保证种群能够向最优解发展。

(10)

3 试验测试

3.1 数据预处理

本研究选取了一组在新疆富满油田某井段实钻作业中记录的现场数据，测量工具累计工作23 h，采样频率为400 Hz。数据集混合不同程度的黏滑振动数据。首先，将井下数据集划分为相同长度的时间窗口，从每个时间窗口自动提取特征。由图1可知，黏滑振动的周期约为9 s，所以设置时间窗口为9 s。然后，通过ISS评价指标计算，将其手动分类为正常钻进、扭转振动、完全黏滑及极端黏滑4种等级。最终得到的数据集包含了上述300组9 s窗口，每组含有3 600个三轴振动测量数据点。由于黏滑被高频事件覆盖，通过移动平均滤波器对数据集进行去噪。对每组时间窗口内的数据进行特征提取，主要操作有：时域分析，提取最大值、最小值、方差、标准差、均值、峰差等15类时域特征；频域分析，对每一个时间窗口进行快速傅里叶变换(FFT)，得到5个频域特征，包括均方频率、频率方差、频率标准差、均方根频率、重心频率；再通过主成分分析(PCA)对特征向量进行降维，以最少的数据维度来充分解释原数据信息。最终得到各个主成分方差解释率以及解释率的变化曲线，如图4所示。

图4 主成分方差解释率以及解释率的变化Fig.4 Principal component variance contribution rate and changes in contribution rate

表2为方差解释，主要是看主成分对于解释变量的贡献率。一般情况下，方差解释率越高，说明该主成分越重要，权重占比也越高。由表2可知，前面8个主成分累计解释率达到了90.849%(一般情况下大于90%即可)，说明使用前8个主成分就能够很好地对黏滑振动等级进行评估。

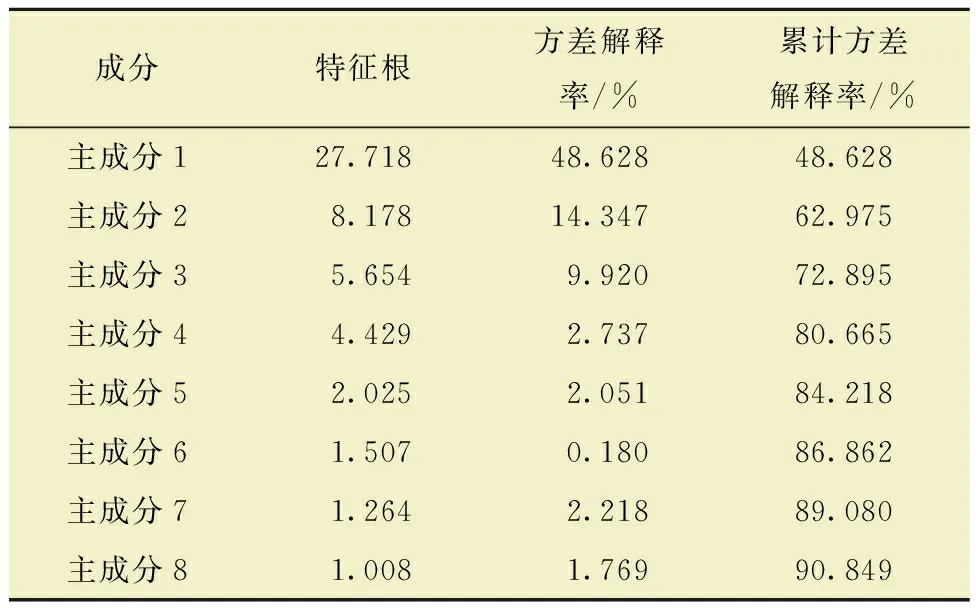
表2 方差解释率Table2 Variance interpretation rate

3.2 建立DE-AWNB算法模型

在传统的贝叶斯算法中，假设每个条件相互独立、互不影响，认为每个属性的重要性一样。在本文中，对传统的NB(朴素贝叶斯)算法模型进行了优化，根据每个特征的重要性赋予不同的权重，通过差分演化算法去寻找最优权重，如图5所示。

图5 DE-AWNB获取权重结构示意图Fig.5 Schematic structure of obtaining weight by DE-AWNB

将DE属性加权应用于NB，得到差分演化算法属性加权朴素贝叶斯(DE-AWNB)模型，整体工作流程见图6。

图6 DE-AWNB整体优化过程Fig.6 Overall optimization process of DE-AWNB

将300组数据集划分为训练集和测试集，采用3重交叉验证方法对数据集进行分类。可将数据集分为3组，每组数据中训练集与测试集的比例为6∶4。

详细的DE-AWNB算法过程描述如表3所示。

3.3 评估结果

表4给出了DE-AWNB模型的评价指标：混淆矩阵、TP(真阳性率)、FP(假阳性率)、Precision(精准率)、Recall(召回率)、F-Measure(F1评分)。这些指标基于一个混淆矩阵，当使用分类模型来预测测试数据的类别时，总共有4种可能(假设这2个类别是真和假)：分类器预测为真，它实际上是真，为真阳性(TP)；分类器预测为真，但实际为假，为假阳性(FP)；分类器预测为假，它实际上是假的，为真阴性(TN)；分类器预测为假，而它实际上是真的，为假阴性(FN)。由表4可知，模型的精准率在86%以上，召回率在79%以上，F1得分整体高于83%，整体模型的平均准确率达到了92.38%。

表4 DE-AWNB模型的评价指标Table4 Evaluation indicators of DE-AWNB model

通过分析发现，模型识别完全黏滑类别时，效果较差，容易被分类为极端黏滑，这可能是极端黏滑振动引起数据的剧烈波动，进而造成的计算误差。以上结果表明，该模型具有较高的精确度，可以有效地进行黏滑振动等级识别。

为了证明DE-AWNB模型在黏滑振动等级评估的优越性，本文使用遗传算法优化属性加权朴素贝叶斯(GA-AWNB)、朴素贝叶斯算法(NB)、随机森林(RF)进行对比分析，结果如图7所示。

图7 模型评价对比图Fig.7 Evaluation comparison of models

图7进一步证明了DE-AWNB模型在收敛时间、整体准确率上优于其他算法。因此，DE-AWNB模型在实际钻井中更适合用于井下黏滑评估。

4 结 论

(1)通过井下近钻头测量参数与地面录井参数的结合，分析得到了衡量黏滑振动的等级指标ISS，并作为机器学习多分类的标签。

(2)针对朴素贝叶斯算法独立条件的局限性，在朴素贝叶斯分类公式中加入了属性权重，并通过差分演化算法寻找最优权重属性，提出了一种更高效的差分演化属性加权朴素贝叶斯(DE-AWNB)改进模型。

(3)将DE-AWNB模型与GA-AWNB、NB、RF模型进行对比，通过模型评价指标，发现DE-AWNB优化模型平均准确率可达92.38%，运算时间可达4.95 s，整体明显优于其他算法。

(4)将该模型应用于实际钻井工程，能够有效提高识别黏滑振动水平，有利于采取及时有效的纠正措施，以提高机械钻速，延长钻头和井下工具的寿命。