随钻涡轮仿真器系统设计*
李 飞 乔 昊
(西安石油大学电子工程学院;中海油集团测井与定向钻井重点实验室定向钻井分室)
0 引 言
油气资源作为我国甚至全球范围内的主要能源,对于全球经济生活具有决定性作用[1]。而近些年来由于全球气候变暖以及当前疫情影响,特别是部分国家及地区持续性的战争导致石油价格上涨。中国石油经济技术研究院发布的《2022—2028年中国石油行业发展策略分析及投资前景研究报告》指出,2020年中国的石油消费总量已达到7.02亿t,比上年同期增加6.6%,未来几年这种情况大概率会呈现持续增长态势[2]。在这种局势下,油气资源的产出早已供不应求。诸多开采技术的各项指标要求也日益提升,其中所需的发电装置相关技术也随之不断被突破。
目前,国内外井下供电主要有电池组供电和涡轮发电机供电2种方式。由于供电技术的不断突破,电池供电方式已经不能满足井下温度上升和反复充放电的工况[3]。而井下涡轮发电机通过钻井液的流动能量来进行循环发电,且其具有高温下工作效率高、工作时限较长、供电的转换率高以及低污染等优势[4],已使其成为井下供电方式的首选。
近年来,井下随钻测量技术(MWD)从钻井工艺参数的测量发展到与随钻测井(LWD)参数相结合,并促使井眼控制手段发生根本性的变化[5]。随着MWD测量参数的增加和井下控制机构的复杂化,油气井开采深度和水平段长度的增加,井温的进一步升高及MWD井下工作时间的延长,MWD电力系统的容量和可靠性成为制约MWD系统正常工作的关键[6]。目前,国外石油公司和钻井服务公司普遍将井下涡轮发电机作为MWD的标准配置。
为保障涡轮发电机井下工作的可靠性,本文以涡轮特性为研究对象,建立随钻涡轮仿真器以永磁同步电机为主的Simulink模型;以永磁同步发电机的数学模型和控制策略为理论基础,通过井下随钻发电机的Simulink模型,建立以DSP为主控制器的同步电机,来模拟实际涡轮的输出特性,以涡轮机驱动发电机的转子旋转产生三相交流电,经整流后输出电能,实现随钻涡轮发电机直流总线电压的闭环控制。通过研究可进一步为随钻涡轮发电机的现场可靠应用提供指导意见。
1 涡轮仿真器的建模与仿真分析
井下钻井液流过涡轮叶片通道,冲击涡轮叶片产生旋转力矩,涡轮主轴与发电机转子直接相连,带动永磁发电机产生三相交流电,经过整流变成直流电,然后经过稳压、滤波供给负载使用。建立的随钻涡轮发电系统的基本结构如图1所示。
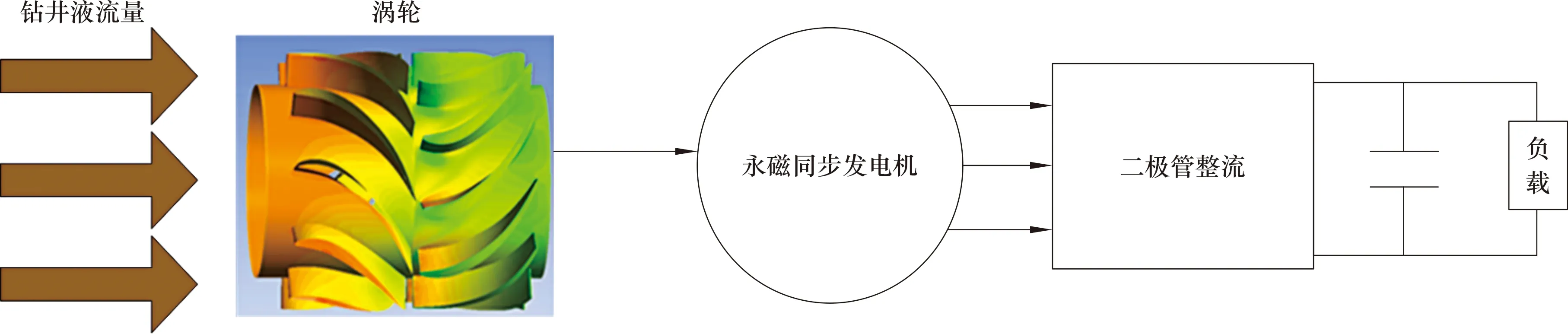
图1 随钻涡轮发电系统图Fig.1 Power generation system of turbine while drilling
永磁涡轮发电系统模型主要包括井下涡轮模型、永磁同步发电机模型、三相二极管桥式整流模型。利用Simulink软件对该涡轮发电模型进行建模和仿真分析。
1.1 涡轮的数学模型
涡轮叶片被钻井液冲击后旋转,将钻井液中的能量转换为机械能,同时产生旋转力矩[7]。根据动量矩定理,涡轮的输出扭矩为:
(1)
其中:
(2)
(3)
S=πD0bφ0
(4)
式中:Ti为涡轮扭矩,N·m;ρ为流体的密度,kg/m3;Qi为流体的流量,L/s;R为计算半径,m;S为涡轮过流面积,m2;i表示不同时刻;n为涡轮转子转速,r/min;α1k为涡轮定子出口角,(°);β2k为涡轮转子出口角,(°);D0为平均直径,m;b为叶片径向高度,m;φ0为考虑叶片厚度影响的断面收缩系数,φ0=0.9。
涡轮的输出功率Pi为:
(5)
式中:w为涡轮转子旋转频率,s-1。
拟合涡轮的Simulink模型如图2所示。设计与实际发电机数据相匹配的涡轮参数为:定子出口角α1k=16.45°,转子出口角β2k=16.45°,涡轮计算半径R=51 mm,叶片高度b=15 mm,密度ρ=1 000 kg/m3,气隙间距d=10 mm。运行涡轮仿真模型,分析在不同流量下涡轮的转速、输出功率和扭矩曲线。
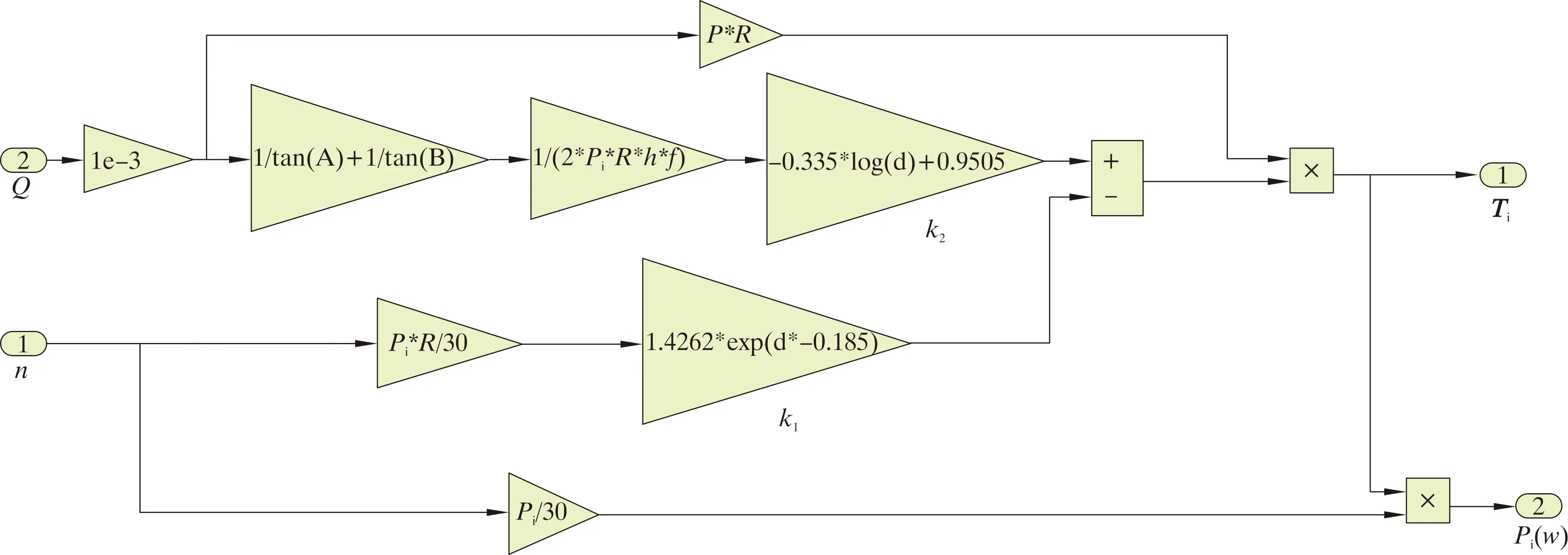
图2 拟合涡轮Simulink模型Fig.2 Simulink model for fitting turbine
1.2 永磁同步发电机的数学模型
永磁同步发电机与涡轮刚性连接,涡轮旋转并带动发电机转子旋转,将机械能转化为电能。永磁同步发电机在两相旋转坐标系下的定子电压方程为[8]:
(6)
式中:id、iq为直轴和交轴电流,A;R为电枢绕组电阻,Ω;Ld、Lq为直轴交轴电感,H;ud、uq为直轴和交轴电压,V;ψf为磁链,Wb;ωe为电机角速度,rad/min。
永磁同步发电机的电磁转矩为[9]:
(7)
式中:Te为电磁扭矩,N·m;np为极对数。
永磁同步发电机的反电势常数为:
(8)

永磁同步发电机的力矩常数为:
(9)
式中:Kt为力矩常数,N·m/A;Ipeak为线电流峰值,A。
由随钻涡轮发电机的工作原理可知,涡轮对永磁发电机直接驱动产生转速,涡轮输出的扭矩可作为永磁发电机的拖动转矩,它可克服永磁发电机的电磁转矩,使永磁发电机转子旋转发电,进而产生电能[10-11]。忽略涡轮与永磁发电机的阻尼系数、摩擦力,进一步得到永磁涡轮发电机的机械运动方程为[12]:
(10)
式中:Tj为惯性扭矩,N·m;Ti为拖动扭矩,N·m;J为涡轮与发电机连接轴间的等效转动惯量,kg·m2;ωm为转子角速度,rad/s。
永磁同步发电机输出有功功率P为[13]:
P=Teωm
(11)
将永磁同步电机作为涡轮机模型的电机驱动,把输入流量转化为扭矩,并经过电流环PI控制驱动随钻发电机进行发电,使其输出性能与涡轮性能近似[14]。永磁同步电机(PMSM)具有结构简单、效率高、功率因数高及低损耗等优势[15-16]。随着永磁同步电机控制技术的不断提高和深入应用,结合实际电机的参数,建立了PMSM的Simulink模型,与涡轮模型组合设计随钻涡轮发电机的驱动模型。该模型以给定的钻井液流量作为涡轮输入参数,经涡轮模型输出响应扭矩,进一步得到参考电流。通过PI控制器调节,输出与涡轮近似的转速,带动随钻发电机转子进行旋转。基于以上公式及原理分析,在Simulink软件中搭建涡轮设计模型,如图3所示。
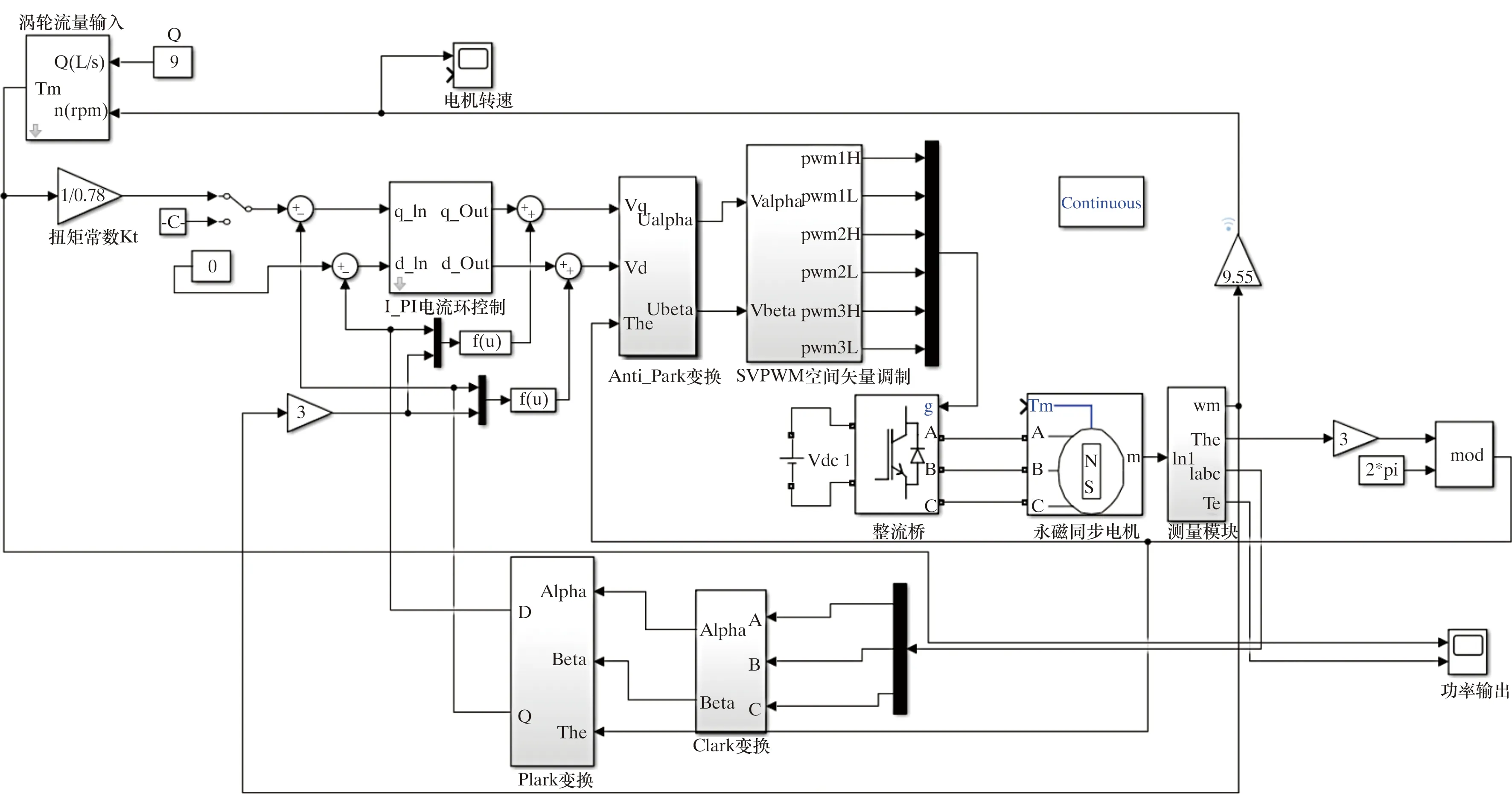
图3 涡轮驱动Simulink设计模型Fig.3 Design of turbine driven Simulink model
1.3 整流模块的数学模型
整流模块采用三相二极管全桥整流电路,由三相半波共阴极接法和三相半波共阳极接法串联组合而成,该模块可将发电机发出的三相电转换成直流电[17]。
整流器的电路图如图4所示。其中Ua、Ub、Uc为三相交流输入侧电压,L为滤波电感,R为等效电阻,VD1~VD6为二级管,Udc为直流侧电压,idc为直流侧电流,C为滤波电容。
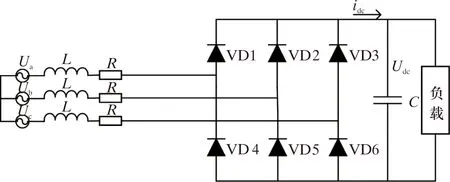
图4 整流器的电路图Fig.4 Circuit diagram of rectifier bridge
直流侧电压的平均值为:
(12)
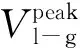
直流侧功率为:
(13)
永磁涡轮发电机的效率为[18]:
(14)
式中:Udc为直流侧电压,V;RL为负载电阻,Ω;Pdc为直流电功率,W。
基于以上理论分析,在Simulink中搭建永磁涡轮发电机的仿真模型如图5所示。系统模块包括涡轮模型、永磁同步发电机模型、整流桥模型。本文使用的永磁发电机的参数为:发电机电阻R=3.35 Ω,定子电感Ld=Lq=0.006 94 H,磁链ψf=0.174 Wb,转动惯量J=0.011 97 kg·m2,极对数np=8。
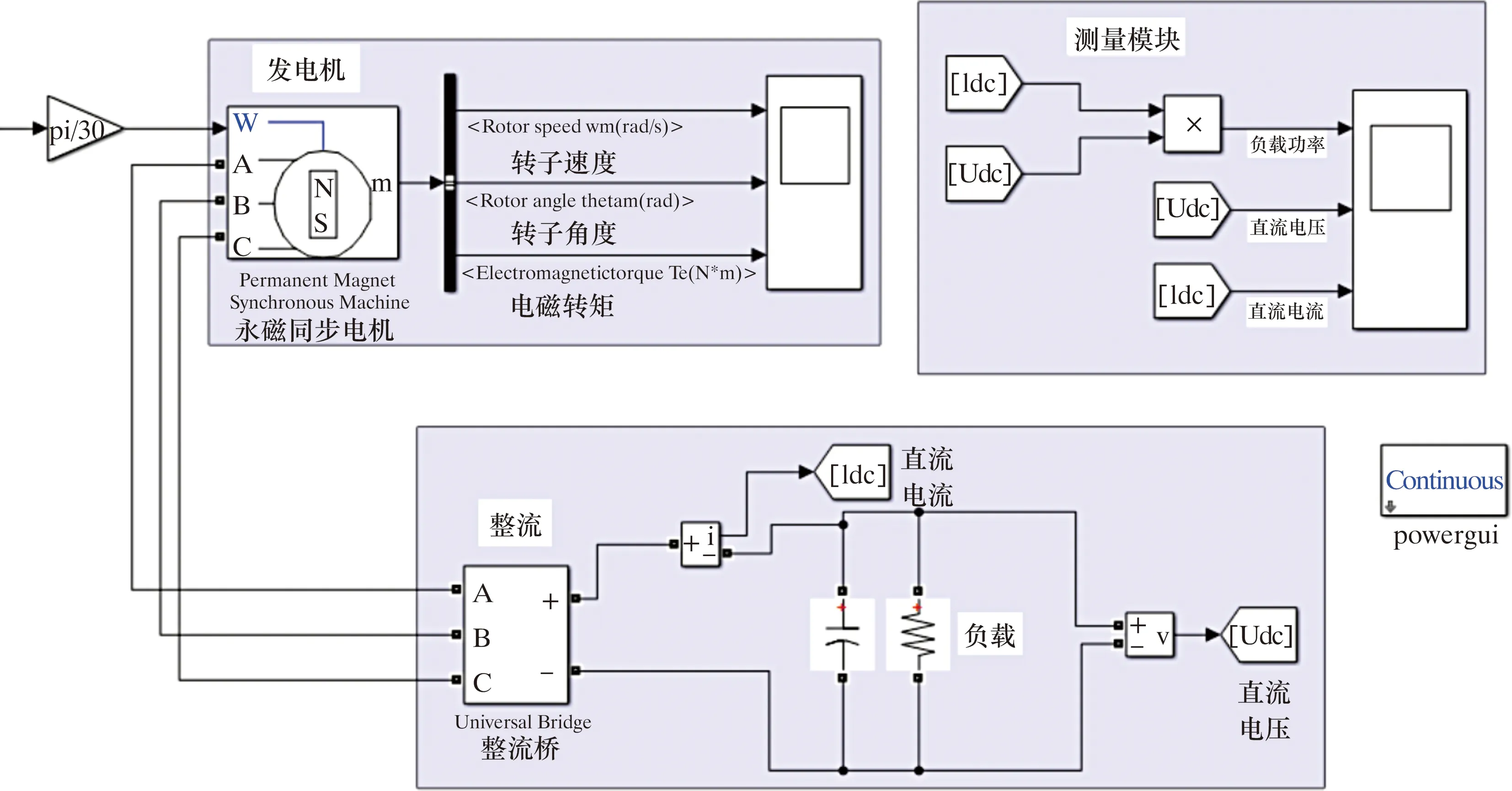
图5 随钻涡轮发电机模型图Fig.5 Model of turbogenerator while drilling
分析其在不同钻井液流量输入下的电机转速以及发电机功率输出情况,表1为在输入流量分别为9.10及11.00 L/s时,不同负载情况下的涡轮发电机输出特性。
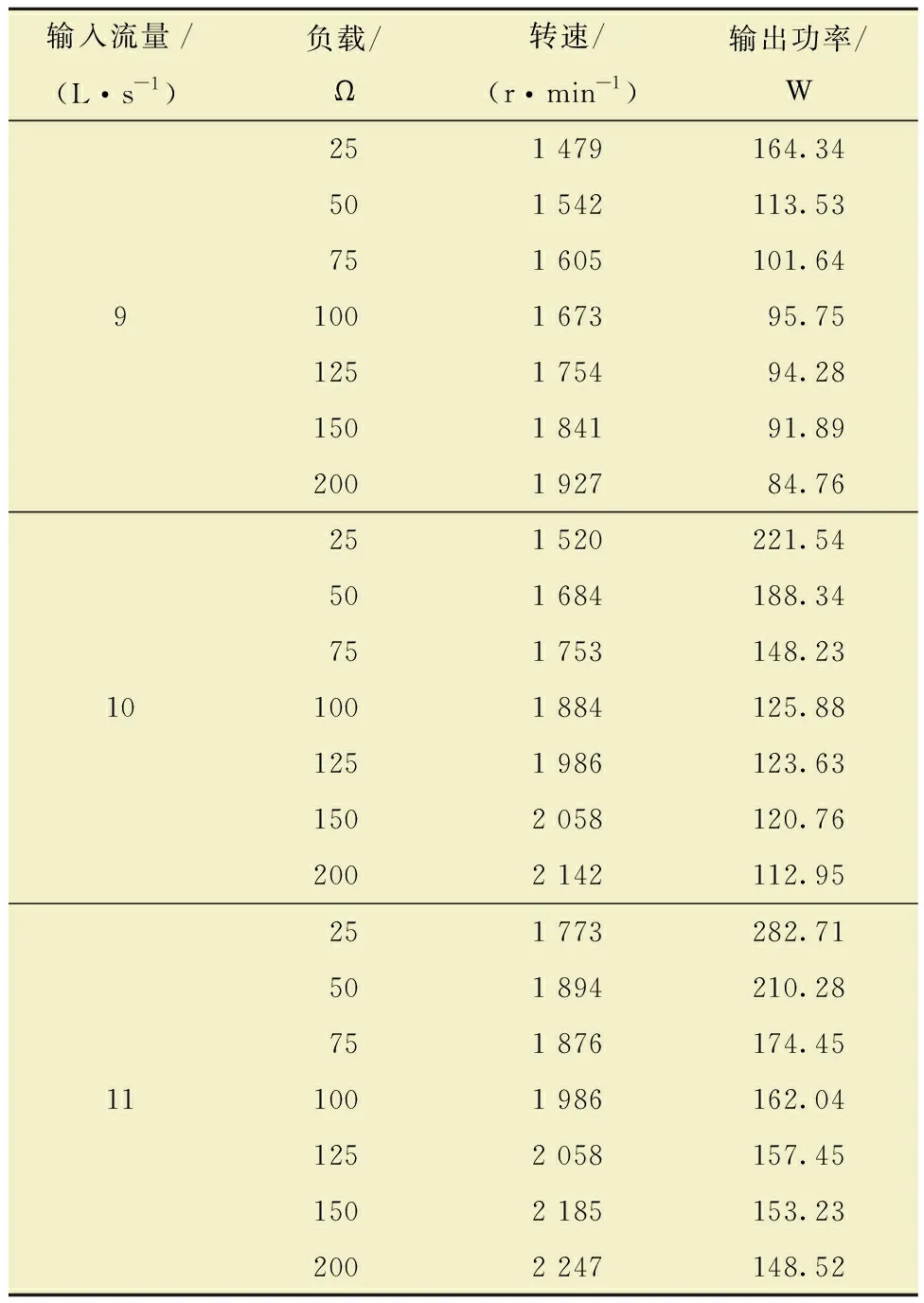
表1 发电机模型输出特性Table1 Output characteristics of generator model
2 涡轮仿真器系统搭建
所采用的仿真系统是基于DSP28335旋变永磁同步电机控制开发板来控制永磁同步电机[19]。电机是电控系统中不可或缺的一种控制装置,针对不同的场合,电机的控制方法也各不相同,而直流电机的PID控制则是最为常用的一种[20-22]。由于PID算法对直流电机的控制较为简单,同时具有良好的驱动性和制动性,所以采用PID算法进行直流电机的DSP控制[23-24]。
2.1 电机驱动电路
电路的DSP控制芯片采用TMS320F28335。本设计采用的旋转变压器永磁同步电机的实物图如图6所示。其电机相关参数如表2所示。
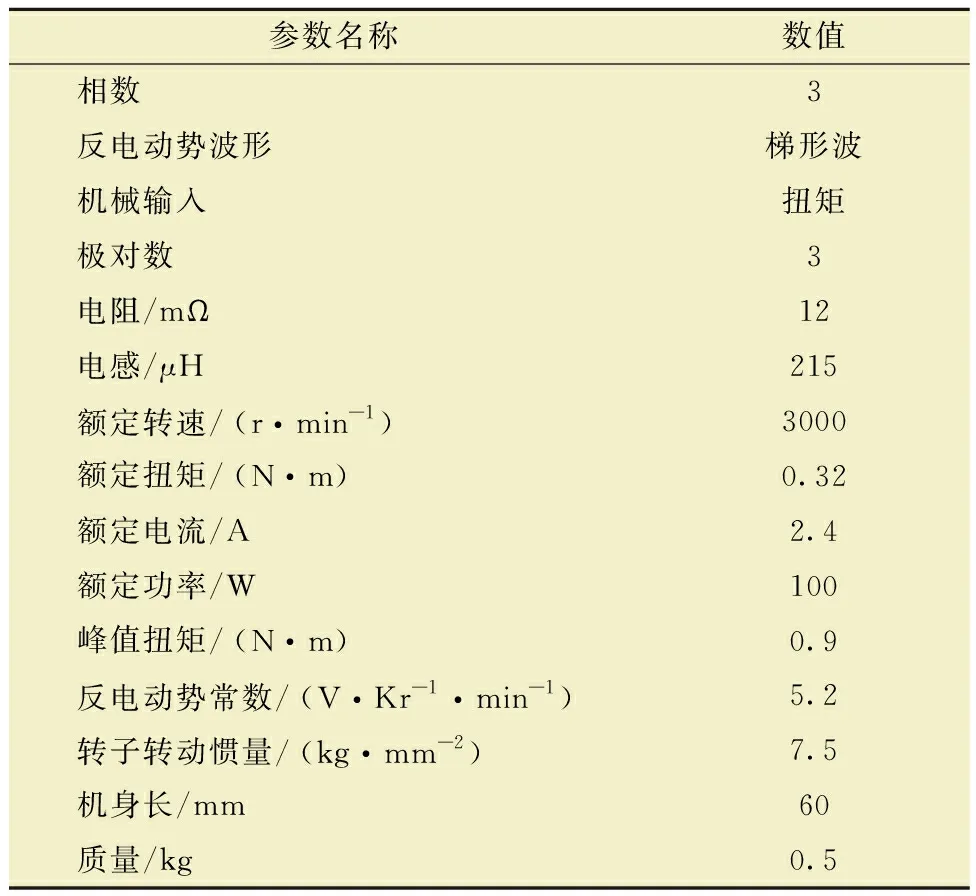
表2 电机参数Table2 Motor parameters

图6 电机实物图Fig.6 Physical picture of motor
为了增强系统的运行性能,首先给出了U相电机驱动电路的模拟电路图,由于V相、W相的电路设计原理与U相电路设计原理一致,所以本文只以U相电路为例进行说明。在U相电路中,PWMUH和PWMUL表示主控制芯片中存在的高位U相电流和低位U相电流的脉冲幅度调制信号[25]。在经过IR2101S芯片后,其Q5、Q7引脚都可以输出与12 V方向相反的方波信号。在Q5输入一个高脉冲信号且在Q7输入端输出一个低脉冲信号,则三极管Q10将被开启,Q9将被关闭。这时电容器C55会受到电压V12P的影响而被充电。Q9引脚输出一个低脉冲时,三极管Q10断开,Q9会重新开启,这时24 V的U相直流电源会通过Q9,使W端口的输出电压提高至36 V,通过驱动电路可以使电机驱动板的运行能力更加高效[26]。图7为U相电机驱动电路图。
将12 V的电压提供给旋转变压器,以达到其输入的差动信号幅值。12 V电压在通过解码芯片时会在输出端同时产生2个3.6 V双振幅信号,因而最终会产生7.2 V双振幅的差分信号。这也相当于如果将解码芯片与单位增益缓冲器相连接,那么在旋转变压器的双振幅输出电压大约为2.06 V时,由于该旋转变压器的激发电压是7 V,则增益缓冲器也将使增益提高。SGM8272的放大电路是由原理图中的电阻R23与R39参与组成的,采用同向比例放大[27]。在该电路中,给连接片设定了约3.8 V的公共模式电压,而激发的公共模式电压是2.6 V左右,最后的缓冲区是6.68 V。D1、Q1的电压应与D2、Q2保持相同。R14和R19的电压也应当是相同的。缓冲电路图如图8所示。
采用电流互感器ACS758LCB-050B对三相电流进行采集,其中U相采集电路如图9所示。该交流变压器的输入电压为40 mV,通过该交流变压器可以对电机的三相电流进行测量,其结果也较为准确。采用电流互感器来对电机的U相电流以及V相电流进行测量,W相电流通过基尔霍夫电流定律来计算[28]。由于U相电流与V相电流均采用了交流变压器来测量,则V相电流的采集电路图与图9相同。

图9 U相电流采集电路Fig.9 U-phase current acquisition circuit
2.2 系统搭建

图10 动态扭矩传感器实物图Fig.10 Physical picture of dynamic torque sensor
通过在实验室搭建测试环境,测试涡轮驱动和发电机输出的系统响应,测试系统如图11所示。
该测试系统由流量给定上位机、永磁同步电机控制电路板、永磁同步电机、永磁同步发电机组成。
所搭建的仿真系统以LabVIEW作为上位机,经过CAN分析仪来进行永磁同步电机的控制,Code Composer Studio作为下位机将与仿真相符的参数指标编译到电机控制板中,接24 V与1.5 A的直流电,经电源供电后,上位机下达指令来进行电机的驱动,待电机转速达到稳定后,上位机即会显示实时的电机转速,而扭矩信号则会经过一个动态扭矩传感器,再以频率信号的方式输出,进而带动发电机发电。搭建的涡轮仿真器系统如图11所示。
3 系统测试与分析
为得到随钻涡轮仿真器整体模型的匹配结果,对涡轮及电机模型进行了仿真分析。当输入钻井液流量Q为5~11 L/s,钻井液密度ρ为1 000 kg/m3时,随钻涡轮发电机系统可以正常运行,其在输入流量9~11 L/s时的输出功率曲线如图 12所示。
从图12可以看出,当输入流量在9~11 L/s时,随着发电机负载的增大,涡轮发电机的输出功率随之缓慢下降,且逐渐稳定下来。由此可以得出,驱动涡轮旋转的输入流量以及负载变化时,发电机输出功率会产生变化,因此可以通过调节流量和负载大小来调整发电机速度稳定后的输出功率。
再对所搭建的系统进行发电机转速测试,同理得出,当输入流量范围为9~11 L/s时,永磁同步电机输出转速曲线如图 13所示。此时,永磁同步电机在不同流量下的输出转速与仿真系统的转速近似。
由上述输入在9~11 L/s的流量条件下涡轮的Simulink模型与仿真系统2个部分的转速特性一致的结论可以得出,在实际的电机驱动过程中,当流量在该范围内时,电机的实际转动效果能被准确有效地测量到。从图12和图13可以看出:当流量保持恒定,增大发电机的负载阻值时,涡轮的输出转速也随之稳步提升,发电机的输出功率会随之逐渐下降;在相同转速条件下,此时的输出扭矩会相应地增大,且2个部分的转速增长趋势基本一致。由此可知,可以通过改变涡轮输入流量的大小来得出涡轮的实际转速与功率,测试试验验证了所搭建的仿真模型的正确性。

图13 输入流量9~11 L/s时发电机系统转速曲线Fig.13 Rotation speed of generator system at input flow rate of 9 to 11 L/s
4 结 论
随着井下各种钻井仪器性能的提升,越来越多的新型电子控制系统被研制,涡轮发电机的使用也日益增加。在钻井过程中,涡轮发电机的实际输出受到钻井液的流体密度和流量等参数的影响。根据实际涡轮特性,通过仿真设计涡轮模型,运用直流电机和PID相关原理,结合实际测量的电机输出数据,设计了涡轮系统仿真模型,研究了涡轮发电机在不同流量范围的输出特性,完成了基于直流电机和DSP的涡轮仿真器设计,得到结论如下:
(1)建立了涡轮驱动设计的Simulink模型,该模型由涡轮Simulink模型和永磁同步电机控制Simulink模型2部分组成,经由电流环PI调节,实现永磁同步电机的扭矩和转速特性与涡轮性能一致。搭建以TMS320F28335为核心的永磁同步电机控制仿真系统,在不同流量下对Simulink模型和系统进行测试,电机的转速在不同流量下的输出性能与涡轮的特性一致,由此实现了实验室环境下随钻涡轮仿真器的初步设计。
(2)根据设计要求,搭建了涡轮机仿真系统,通过电机控制的流程,将所设计的仿真模型结果与实际工作数据进行了比较分析,并完成了仿真模型与实际系统之间的比较。
(3)比较了直流电机与涡轮模型输出特性,在试验中经过测量得出,在输入流量为5~11 L/s时,涡轮的输出特性有很好体现,由此验证了涡轮仿真器的正确性。所得结论为涡轮机的后续研究提供了参考,对现场操作具有指导意义。

