深水无隔水管钻井钻柱三维振动响应特性研究*

柳军 陈飞宇 李建 郭晓强

(西南石油大学机电工程学院)

0 引 言

随着海上油气田开采技术的日渐成熟，浅海油气资源被陆续开发，现在世界主要国家开始开采深海油气资源[1]。无隔水管钻井技术不采用常规海洋钻柱隔水管系统，可降低钻井成本，但使钻柱系统面临了更多的挑战[2-3]。在无隔水管钻井过程中，海水段钻柱系统受到外部海洋载荷、顶部转盘扭矩以及底部钻头-地层作用力影响，极易发生纵-横-扭三个方向的振动，导致钻柱发生强度降低、磨损及疲劳失效。为此，亟需开展无隔水管钻井钻柱振动问题研究。

早期钻柱研究主要集中于陆地常规钻柱振动，建立了钻柱系统纵向受迫振动模型[4-6]。高宝奎等[7]研究了钻柱的横向振动机理，发现底部钻具组合发生屈曲是钻柱横向振动的来源。祝效华等[8]基于Hamilton原理和有限元理论，构建了纵-横-扭耦合的钻柱振动力学模型。在浅海常规钻柱振动研究方面，R.J.ADAMS等[9]以墨西哥湾深水区为例，进行了海洋环境下管柱设计。 S.D.EVERAGE等[10]研究了海洋环境下，钻柱下入过程中海浪激励时钻柱动态轴向载荷，并建立了计算模型。在无隔水管钻井钻柱振动特性研究方面，韩涛等[11]分析了无隔水管钻井钻柱的作业环境对钻柱振动的影响，建立了海流速度分布模型。江文龙等[12]建立了无隔水管钻井稳态温度计算模型和ECD计算模型。夏开朗等[13]建立了深海钻探船-钻井液返回管线系统模型，分析了返回管线的动态特性。王杰[14]研究了平台偏移量对无隔水管钻井钻柱振动的影响，在忽略钻柱转动的情况下建立了横向振动模型和瞬态涡动力学模型。黄剑等[15]分析了不同因素下钻柱运动规律和应力分布情况，建立了无隔水管钻井钻柱在非线性支承下的力学模型。

以上研究主要分析了海水段的钻柱振动，忽略了地层段的振动，实际上钻柱只是在井口受到横向约束，有必要分析地层段的钻柱振动情况。多数研究在分析海流时，都将钻柱考虑成静止的圆柱绕流问题，而静止的圆柱绕流现象与旋转中的钻柱有明显不同，圆柱旋转会改变均流升力系数[16]，改变钻柱的转速，进而影响钻柱的振动[17]，所以在研究钻柱的振动响应时，应该考虑钻柱转速对钻柱振动的影响。为此，本文基于能量法、Hamilton变分、微元法和达朗贝尔原理，在考虑海流、钻井液流速和钻柱-井壁接触碰撞等因素的基础上，建立了无隔水管钻井钻柱的三维振动方程，并验证其有效性，同时分析了无隔水管钻井钻柱的振动响应。所得结论可为无隔水管钻井钻柱的减振措施制定提供参考。

1 无隔水管钻井钻柱振动模型

1.1 钻柱横向振动方程

无隔水管钻井钻柱在海流和波浪的影响下会产生横向振动，顺流向表现为拖曵力，横流向表现为升力。为了分析钻柱的横向振动，建立如图1所示的坐标系。

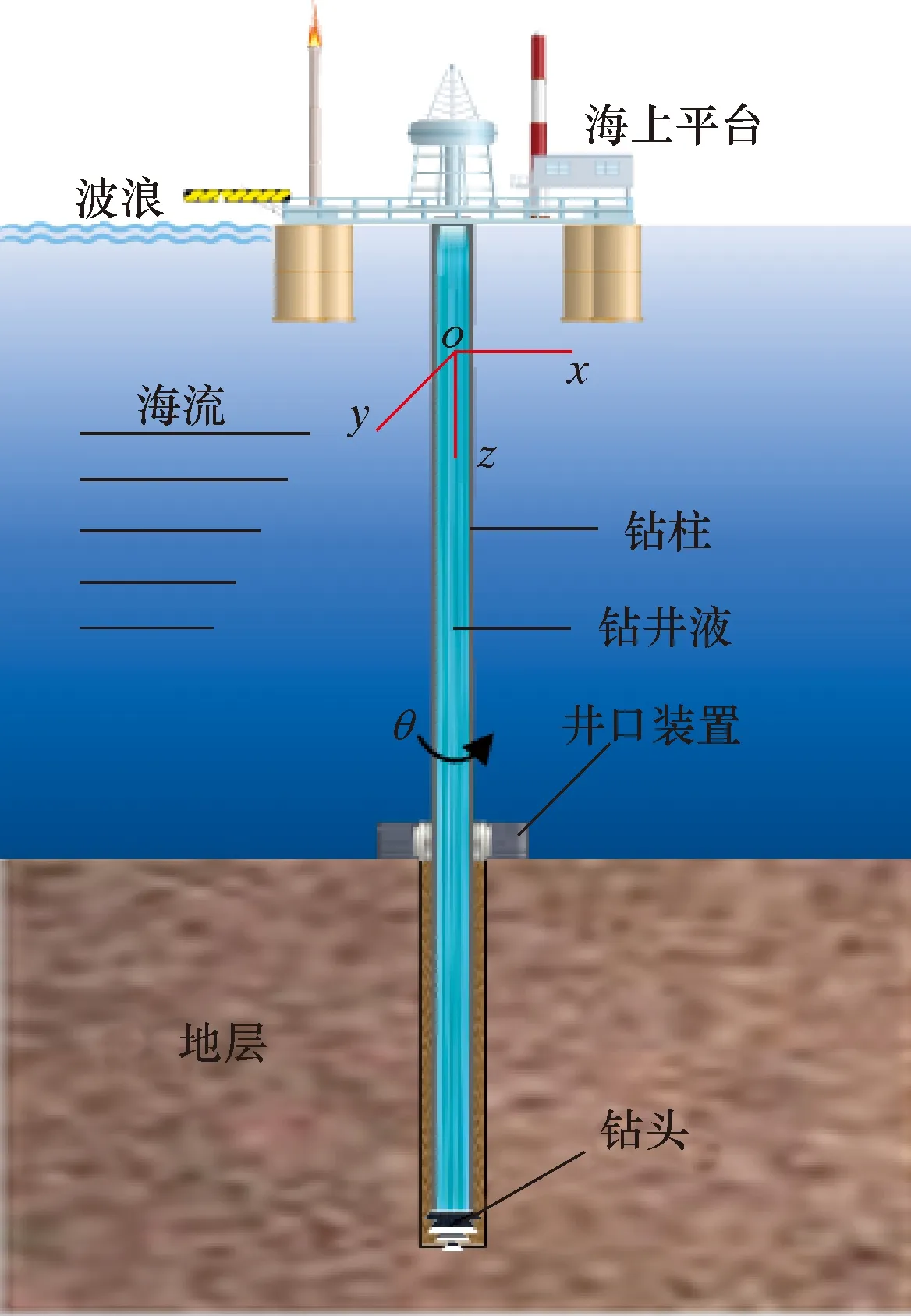
图1 无隔水管钻柱坐标系示意图Fig.1 Schematic diagram of coordinate system for riserless drill string

图1中，令钻柱上端处为坐标原点，顺流向为x轴，横流向为y轴，钻柱竖直方向为z轴；设钻柱沿x轴的变形为u，沿y轴的变形为v，取钻柱初始位置处长度为dz的钻柱单元，经过振动变形，钻柱单元的长度变为ds，则钻柱单元的纵向应变ε可表示为：

(1)

式中：ε0为钻柱单元的线性应变。

将式(1)变分可得:

δε=u′δu′+v′δv′

(2)

钻柱的轴向应变能可以表示为：

(3)

将钻柱的轴向应变能变分后可表示为：

(4)

式中：E表示弹性模量，A表示钻柱横截面积，T表示钻柱的有效轴向力，L表示钻柱总长。

圆柱单元曲率可表示为к=u″+v″，其变分为：

δк=δu″+δv″

(5)

将钻柱弯曲应变能进行变分，于是有：

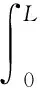
(6)

钻柱惯性力所做的虚功可表示为：

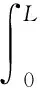
(7)

FD为波浪和海流共同作用下钻柱顺流向的拖曳力，FL为海流作用下钻柱横流向所受的升力。钻柱阻尼力所做的功与外力对钻柱所做的功可分别表示为：

(8)

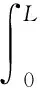
(9)

式中：c为钻柱振动阻尼。

根据Morison方程，任意深度z处作用的水平波浪力可以表示为：

(10)

根据Airy波理论，波形方程为：

(11)

速度和加速度分别为：

(12)

(13)

式中：k为波数，t为波峰通过原点后的时间，T1为周期，ω为波频，H为波高，x为水质点的水平位移。

联合波浪力，可以得到钻柱顺流向所受拖曳力和横流向所受升力的表达式：

(14)

式中：CL为海流的升力系数，CD为海流的阻力系数；Uc为海流质点速度(海流速度)。

根据功能平衡关系：

δU1+δU2+δW1+δW2+δW3=0

(15)

将式(4)～式(14)代入式(15),可得无隔水管钻井钻柱横向振动方程：

(16)

边界条件如下：

(17)

(18)

(19)

式中：L1表示海水段钻柱长度。

1.2 无隔水管钻井钻柱纵向振动方程

为了分析钻柱的纵向振动，对实际情况进行了简化分析，钻柱纵向振动物理模型如图2所示，用m1、k1分别模拟无隔水管钻井钻柱上端悬挂的总成质量和刚度，用m2、k2分别模拟钻柱下端减振器的质量和刚度。

图2 钻柱纵向振动物理模型Fig.2 Physical model of longitudinal vibration of drill string

根据物理模型，采用微元法，可以得到无隔水管钻井钻柱纵向振动控制方程：

(20)

移项可得：

(21)

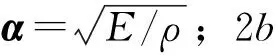
当b=0时，钻柱纵向无阻尼自由振动方程为：

(22)

采用分离变量法可得方程的通解：

w(z，t)=[A′sin(ω1t)+Bcos(ω1t)]×

(23)

式中：ω1为钻柱系统的固有频率，A′、B、C和D均为未定参数，由初始条件和边界条件确定。

图2中的钻柱上、下端和变截面处的边界条件可以如下表示。

在悬挂端(z1=0)：

(24)

在钻柱与钻铤变截面处(z1=l1、z2=0)：

(25)

(26)

在钻柱下端(z2=l2)：

(27)

式中:A1为钻杆的横截面积，A2为钻铤的横截面积。

1.3 无隔水管钻井钻柱扭转振动方程

为了分析钻柱的扭转振动形式，笔者将钻柱的扭转进行简化，钻柱扭转振动模型如图3所示。

图3 钻柱扭转振动模型Fig.3 Model of torsional vibration of drill string

扭转角和扭矩之间的关系可以表示为：

(28)

式中：G为切变模量，Ip为钻柱横截面的极惯性矩。

由达朗贝尔原理可得无隔水管钻井钻柱的扭转振动方程：

(29)

式中：J为钻柱的转动惯量。

J=ρIpdz

(30)

将式(28)和式(30)代入式(29)，可得：

(31)

(32)

式中:ω2为钻柱的转速，r/min。

A3和B3为未定参数，由钻柱边界条件确定。钻柱扭转振动边界条件为：

(33)

1.4 模型计算方法

本文参考柳军等[18]的有限元分析方法对上述模型进行分析，并采用Fortran软件分别编写了无隔水管钻井钻柱横向、纵向和扭转振动计算的Fortran代码；在求解时，通过判断地层段钻柱位移是否大于钻井空间间隙来确定钻柱和井壁的接触，算法原理和计算过程如下：

(1)确定i时刻的位移、速度和加速度；

(2)生成i时刻钻柱整体刚度矩阵、质量矩阵和阻尼矩阵；

(3)确定时间步长Δt，参数β和γ，并计算积分常数；

(4)计算等效刚度矩阵；

(5)计算i+1时刻的等效载荷和位移；

(6)计算i+1时刻的加速度和速度；

(7)将i+1时刻的位移、速度和加速度，作为下一时刻的初始条件，重复步骤(1)～(6)，直至时间循环结束。

图4为钻柱三维模型求解流程图。

图4 钻柱三维模型求解流程图Fig.4 Solution process of three-dimentional model of drill string

1.5 算例验证

本文采用文献[19]中的试验模型数据进行算例验证，具体参数为：钻柱长度6.3 m，水深6.3 m，钻柱外径25 mm，壁厚1.5 mm，外流密度1 000 kg/m3，钻柱密度2 178 kg/m3，外流流速0.35 m/s，内流密度1 000 kg/m3，弹性模量108 GPa，内流流速0.3 m/s。根据数据可计算出流体的雷诺数为8 750，阻力系数和升力系数则选用王亚玲等[20]进行的雷诺数为104以下圆柱绕流的流体仿真结果。图5为本文所建模型计算的钻柱中点处横向位移时程曲线。由图5可知，模型计算的位移与文献[19]的试验数据基本一致，从而验证了本文模型的有效性。

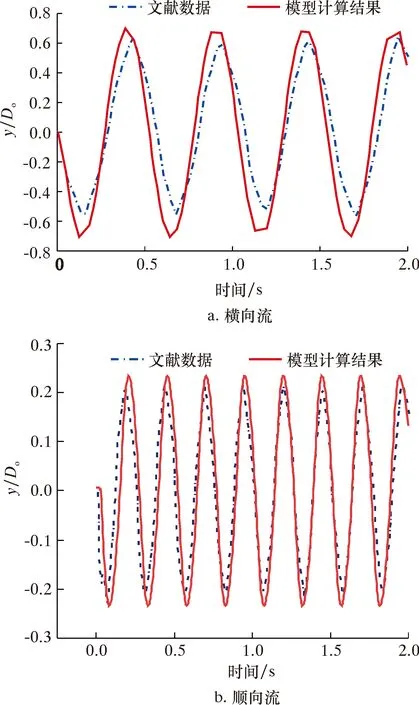
图5 钻柱中点处横向位移时程曲线Fig.5 Time-history curve of lateral displacement at the midpoint of drill string

采用张海莉[21]使用的实际钻井参数作为计算案例，具体参数为：钻柱总长1 000/2 000 m，钻杆长度760/1 760 m，钻铤长度240 m，钻杆根数426，钻铤根数26，钻杆横截面积0.003 5 m2，钻铤横截面积0.015 9 m2，钻柱密度7 850 kg/m3，重力加速度9.8 m/s2，弹性模量210 GPa，减振器刚度4.910 6 N/m，计算钻柱纵向无阻尼自由振动固有频率。通过计算，得到钻柱纵向振动前10阶固有频率，并与文献[21]中的解析解进行对比，结果如图6所示。由图6可知，本文模型得到的固有频率值可以很好地匹配文献中给出的解析结果。

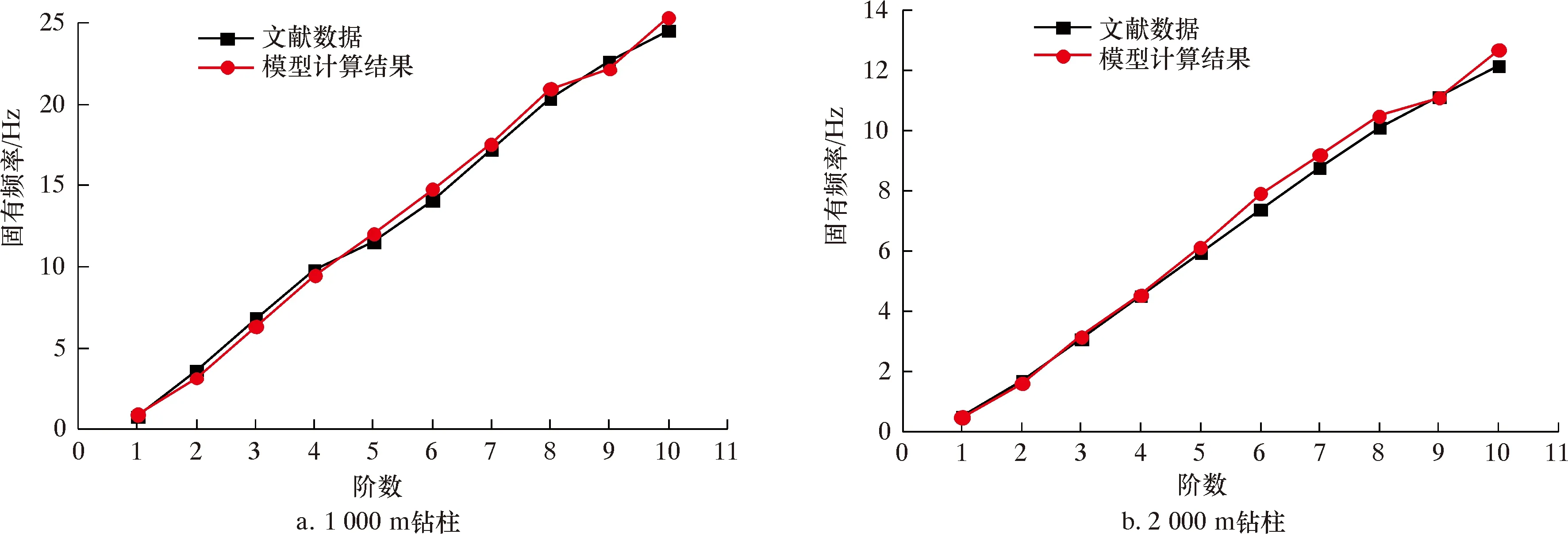
图6 不同长度钻柱纵向振动固有频率Fig.6 Natural frequencies of longitudinal vibration of drilling strings with different lengths

采用杨尧焜[22]的钻柱参数作为案例，具体参数为：ø66.04 cm钻头，ø159(70)mm钻铤，ø127(108) mm钻杆，弹性模量206 GPa。通过计算长度为1 000和1 500 m的钻柱系统，得到钻柱纵向振动前8阶固有频率，并与文献[22]中的解析解进行对比，结果如图7所示。由图7可知，分析得到的固有频率值可以很好地匹配文献中给出的解析结果。

图7 不同长度钻柱扭转振动固有频率Fig.7 Natural frequencies of torsional vibration of drilling strings with different lengths

2 无隔水管钻井钻柱振动响应分析

根据文献[21-23]所设置的钻柱参数，确定本文的基本计算参数：钻柱长度1 000 m，水深600 m，钻柱材料密度8 700 kg/m3，钻井液密度1 198 kg/m3，海水密度1 030 kg/m3，钻井液流速3.0 m/s，钻柱内径131.0 mm，钻柱外径149.2 mm，井眼直径444.5 mm，重力加速度9.8 m/s2，弹性模量210 GPa，附加质量系数1.0，钩载200 kN，雷诺数100～300，摩擦因数0.3，海水动力黏性系数0.001 Pa·s，结构阻尼系数0.1和0.001，速度比1.0～4.0，钻压90 kN，平均钻压100 kN，波动钻压10 kN，牙轮个数3，转速60 r/mim，悬挂刚度9×106N/m，减振器刚度5×106N/m。由于高雷诺数时圆柱周围流体具有明显的三维特性，不同断面的升力和阻力系数并不相同[20]，所以笔者选择低雷诺数流体参数计算并分析无隔水管钻井钻柱横向振动响应。

2.1 无隔水管钻井钻柱横向振动响应

2.1.1 雷诺数对横向振动的影响

无隔水管钻井钻柱不同于常规钻井钻柱，洋流会对钻柱进行激励，使钻柱发生横向振动，横向的激励分别与阻力系数和升力系数相关，而阻力和升力系数又与雷诺数相关，参考文献[24]，选取雷诺数为100、200和300时的阻力系数与升力系数。

图8为不同雷诺数下无隔水管钻井钻柱的横向流和顺向流振动位移响应包络图。图9表示无隔水管钻井钻柱在不同雷诺数下不同位置处的最大弯曲应力。由图8和图9可知，钻柱横向流的振动响应远小于顺向流，这表明洋流产生的拖曳力对钻柱产生的影响要大于其升力对钻柱产生的影响。由图8b可知，在海水段，钻柱的顺向流振幅随海水深度的增加而减小，而不同雷诺数的钻柱振动曲线趋于一致。由图9a可知，随着雷诺数的增加，钻柱的横向流最大弯曲应力相应增大，横向流的最大弯曲应力在海底井口出现最大值。由图9b可知，随着海水深度的增加，钻柱的顺向流最大弯曲应力相应减小，在到达海底时，陡降到最小。这是因为井口装置会限制钻柱的横向位移，离井口装置越远的钻柱位移越大，而钻柱的顺向流位移主要受洋流的拖曳力影响，故顺向流的位移不受雷诺数影响。对于现场钻柱来说，更应该关注海水段受到拖曳力的影响。

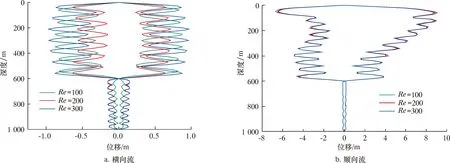
图8 不同雷诺数下钻柱横向振动位移包络图Fig.8 Envelope diagram of lateral vibration displacement of drill string under different Reynolds numbers

图9 不同雷诺数下钻柱横向振动最大弯曲应力Fig.9 Maximum bending stress of lateral vibration of drill string under different Reynolds numbers

2.1.2 速度比对横向振动的影响

由于流体存在旋转绕柱现象，升力系数会随着钻柱转速的改变而改变，所以采用速度比λ(λ=ω2Do/(2Uc))的变化来研究转速与升力系数的关系[25]。为研究钻柱转度和海流速度对钻柱横向振动的影响，本文选取不同速度比下的升力系数代入振动模型。因为转速主要影响升力系数，所以本文只研究转速对横向流振动的影响。参考文献[25]，本文的速度比λ取1.0～4.0。

图10 不同速度比下钻柱横向流振动位移包络图Fig.10 Envelope diagram of lateral vibration displacementof drill string under different speed ratios

图10为不同速度比下的无隔水管钻井钻柱横向流振动位移包络图。图11为不同速度比下无隔水管钻井钻柱横向流最大弯曲应力图。由图10可知：当λ=2.0时，海水段钻柱同一位置的振动幅值最小；另外，除了速度比为2.0，振动幅值随着速度比的减小而增大，这说明速度比为2.0是一个转折点，而在地层段，由于井壁的约束，各个速度比下的振幅基本一致，且振幅都较小。从图11可以看出，随着速度比的增大，钻柱的最大弯曲应力先减小后增大，而在速度比为1.0时，最大弯曲应力最大，在速度比为2.0时，最大弯曲应力最小。这表明适当增大速度比会减小海流对钻柱的激励作用，现场最好在速度比为2.0的情况下运行钻柱。

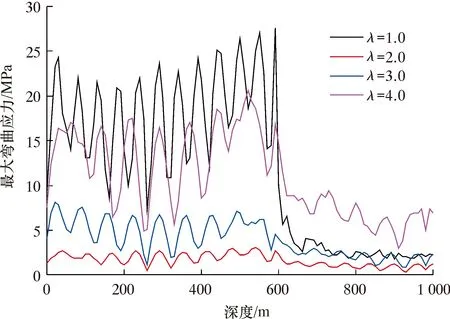
图11 不同速度比下钻柱横向流最大弯曲应力图Fig.11 Maximum bending stress of lateral vibration of drill string under different speed ratios

2.1.3 钻井液流速对横向振动的影响

为研究钻井液流速对钻柱横向振动的影响，取雷诺数为100时的升力系数和阻力系数，取钻井液流速v1=3、6和9 m/s，分别代入无隔水管钻井钻柱横向振动模型，计算得到无隔水管钻井钻柱最大弯曲应力，如图12所示。由图12a可知:钻柱的横向流最大弯曲应力随着钻井液流速的增加而增大，且在海水段都呈现两端大、中间小的趋势；随着钻井液流速的增加，越靠近分界处，增加量越大，而地层段的变化幅值不大。由图12b可知，随着海水深度的增加，钻柱的顺向流最大弯矩和弯曲应力整体都逐渐减小，在海底井口位置陡降，并继续随着深度的下降而缓慢下降，且海水段钻柱顺向流最大弯矩远大于地层段。但是，在钻井液流速v1=9 m/s时，钻柱顺向流的弯矩和弯曲应力呈先减小后增大再减小的趋势，在深度300 m左右出现了较大的上升趋势，随后下降，这表明钻井液流速较大时会对钻柱振动有较大影响。

图12 不同钻井液流速下钻柱横向振动最大弯曲应力Fig.12 Maximum bending stress of lateral vibration of drill string under different drilling fluid flow rates

2.2 无隔水管钻井钻柱纵向振动响应

2.2.1 波动钻压对纵向振动的影响

为分析波动钻压对钻柱纵向振动响应的影响，将钻压幅值分别为10、15、20和25 kN代入无隔水管钻井钻柱纵向振动模型，得到钻柱中点处的纵向振动位移时程响应和幅频曲线，如图13所示。

图13 不同波动钻压下钻柱中点处纵向位移时程响应和幅频曲线Fig.13 Longitudinal displacement response and amplitude-frequency curve at the midpoint of drill string under different fluctuating WOBs

由图13a可知，随着波动钻压幅值的增大，钻柱的纵向振动位移响应增大，这是因为钻压越大，钻柱的轴向冲击就越大，故钻柱轴向应力随之增大。由图13b可知，钻柱纵向振动频率基本不受钻压幅值变化的影响，表明现场钻柱可采用较小的波动钻压。

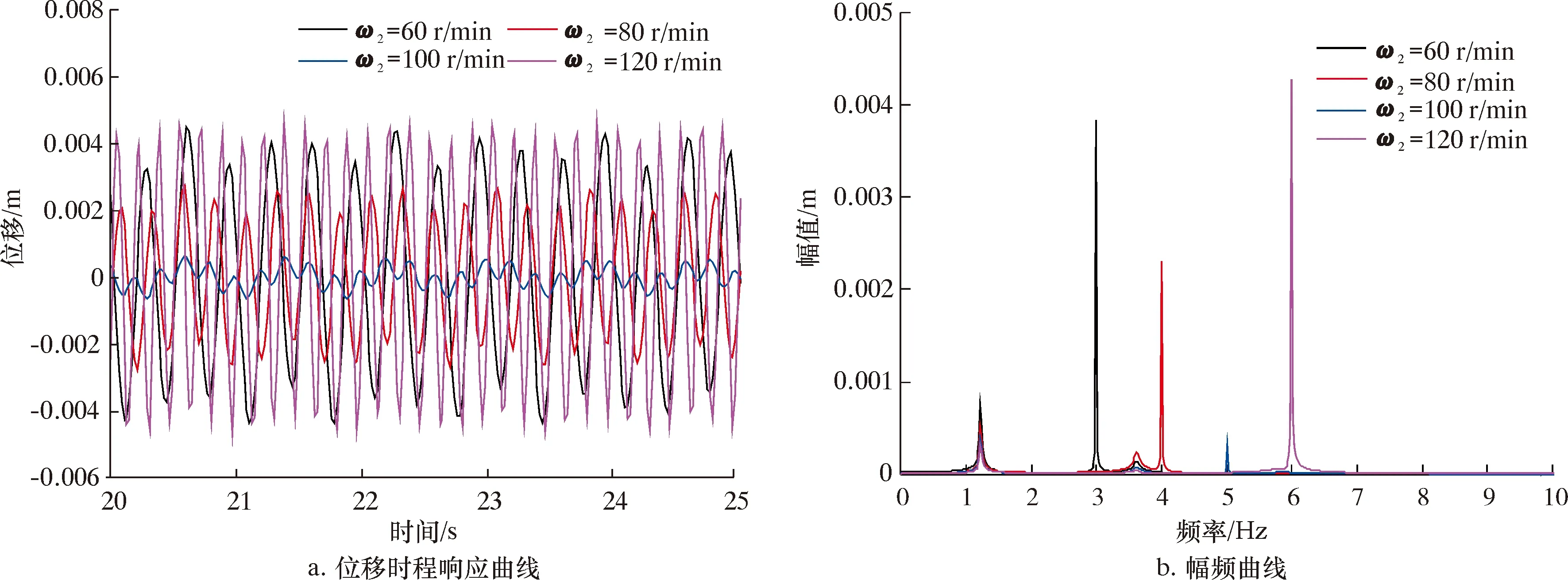
图14 不同转速下钻柱中点处纵向位移时程响应和幅频曲线Fig.14 Time-history response and amplitude-frequency curve of longitudinal displacement at the midpoint of drill string at different rotary speeds

2.2.2 转速对纵向振动的影响

为了分析转速对无隔水管钻井钻柱纵向振动响应的影响，分别设置转速为60、80、100和120 r/min，代入钻柱纵向振动模型中，得到钻柱中点处的纵向位移时程响应和幅频曲线，如图14所示。由图14a可知，转速从60 r/min增加到100 r/min时，钻柱的纵向振动位移逐渐减小，而在转速增加到120 r/min后，钻柱的纵向振动响应陡然增大，结合幅频曲线可以看出，这是不同的转速导致钻柱处于不同的振动频率，在转速为120 r/min时，钻柱的振动频率接近第3阶固有频率，此时钻柱处于纵向共振状态，故纵向振动响应突然增大。以上表明，现场钻柱可以通过适当增加转速来减轻钻柱纵向振动，但应该避开120 r/min的转速。

2.3 无隔水管钻井钻柱扭转振动响应

2.3.1 波动钻压对扭转振动的影响

钻柱的扭转振动与纵向振动具有相似性，为分析不同波动钻压下钻柱的扭转振动响应，同样选取波动钻压幅值分别为10、15、20和25 kN，代入钻柱的扭转振动模型中，得到不同波动钻压下钻柱最大扭转角，如图15所示。

图15 不同波动钻压下钻柱最大扭转角Fig.15 Maximum torsional angle of drill string under different fluctuating WOBs

由图15可知，随波动钻压幅值的增大，同一位置处的扭转角响应随之增大，在钻柱约和处的扭转角响应最小，产生的剪切应力最大。这表明现场钻柱可通过减小波动钻压来减小钻柱的扭转剪切应力，应特别注意钻柱的和处。

2.3.2 转速对扭转振动的影响

为分析不同转速下的无隔水管钻井钻柱扭转振动响应，分别计算出钻柱同一位置转速为60、80、100和120 r/min时的扭转振动响应，结果如图16所示。由图16可知，钻柱同一位置的最大扭转角幅值随转速的增加而减小，当钻柱转速超过100 r/min后，最大扭转角不再减小，而扭转角响应波峰个数都随转速的增加而增多，钻柱在转速为60 r/min时扭转角最大，此时造成的剪切应力最大，现场应避免钻柱在此转速作业。

图16 不同转速下钻柱最大扭转角Fig.16 Maximum torsional angle of drill string under different rotary speeds

3 结 论

(1)考虑浪流、钻井液流速和钻柱-井壁接触碰撞等因素，基于能量法建立了无隔水管钻井钻柱的横向振动控制方程；基于微元法和达朗贝尔原理，分别建立了钻头与地层作用下的无隔水管钻井钻柱纵向和扭转振动模型，并对钻柱振动模型进行验证，结果表明本文建立的模型有效，匹配性好。

(2)分析了雷诺数、速度比和钻井液流速对钻柱横向振动响应的影响。分析结果表明，地层段钻柱的振动响应远没有海水段的大，并且横向流振动幅值也要小于顺向流振动幅值，但其振动频率却大于顺向流的。洋流产生的拖曳力对钻柱产生的影响要大于升力对钻柱产生的影响，对于现场钻柱来说，更应该关注海水段钻柱受到的拖曳力影响，适当增大速度比会减小海流对钻柱的激励作用，钻井液流速较高时会对钻柱振动产生较大影响。

(3)分析了波动钻压和转速对钻柱的纵向和扭转振动响应的影响，波动钻压幅值影响钻柱纵向振动的位移响应，但不会影响纵向振动频率。现场钻柱可采用较小的波动钻压，以减小钻柱的纵向振动和扭转剪切应力；可通过减小波动钻压和适当增加转速来减轻钻柱纵向振动，但应该避开120和60 r/min的转速。