固液耦合工况下钻柱的扭振频率分析

肖文生，刘忠砚，王鸿雁，王现峰，付雷，殷有财

（中国石油大学（华东）机电工程学院，山东青岛 266580）①

钻柱是钻井工程中十分重要的部件，在钻井过程中，钻柱将钻头送至井眼底部并向钻头传递动力，同时伴随有各种振动和冲击，给钻井施工带来不利影响［1－3］。钻柱在恶劣的环境中产生的动力学效应，不仅导致钻具失效和钻井事故的发生，而且还严重影响井眼轨迹的控制［4－6］，提高了钻井成本。

钻柱的扭转振动是指钻柱绕其中心线的旋转运动，该振动产生的原因是钻头间歇破碎岩石时所产生的变化速度［7］。钻柱固液耦合工况下的振动固有频率及振动模态分析是研究钻柱动力学特性的基础，是顶驱钻井法钻柱动力学的基础研究［8］。国外固液耦合理论已经比较成熟。国内，李子丰等［9］针对钻柱的扭转问题分别建立了转矩激励法和转角激励法的钻柱扭振动力学模型；江进国等［10］利用ANSYS有限元软件对钻杆进行了扭振分析，得到了钻杆壁厚、钻柱长度等因素对钻杆固有频率的影响，但未考虑钻柱的实际固液耦合工作环境。笔者建立了固液耦合工况下的钻柱动力学方程［11］，并且利用ANSYS有限元软件模拟了钻柱扭转振动的实际固液耦合工作环境，分析了钻井液、钻铤长度等因素对钻柱扭转振动的影响，分析结果对提高钻井效率、降低钻井成本有着重要的实际工程意义。

1 钻柱扭转振动分析

1.1 钻柱模态分析

通过模态分析可以掌握井下多体钻柱在一定频率范围内的主要模态特性，预测各种振源作用下的实际振动响应［12］

钻柱无阻尼自由振动矩阵方程为

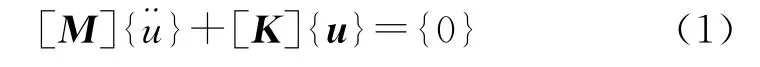
式中：［M］为质量矩阵；［K］为刚度矩阵；u为结构位移向量。

设定钻柱的固有频率为f，则钻柱广义固有频率方程为

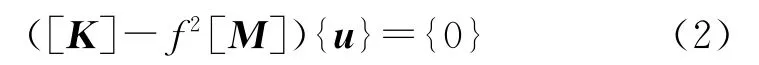
为求得式（2）的非零解，应使特征矩阵［K］－f2［M］等于零，即

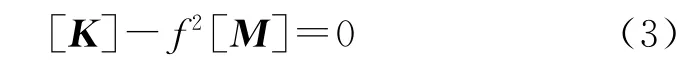
将特征矩阵展开，得到关于固有频率f2的n次代数方程。求出这个方程的n 个根，从而得到n 个自振频率fi（i＝1，2，…，n）。将fi代入式（1），进而求得n个主振型向量｛ui｝，即井下钻柱的n 个固有振型。

1.2 钻柱扭转振动临界转速

当其和钻杆的扭转振动固有角频率ω相近时发生共振，故有ω＝nπ／30，即引起钻杆共振的临界转速为

式中：ωi为系统扭转振动的第i 阶固有角频率，rad／s。

若将式（4）中固有角频率ωi换算成固有频率fi，则可以表示成：

式中：fi为系统扭转振动的第i阶固有频率，Hz。

1.3 钻柱ANSYS有限元分析

1.3.1 建立有限元模型

建立了比较符合实际工况的钻柱模型，如图1所示。将井架等地面系统简化为1个Spring单元和1个Mass单元；将钻头简化为1个集中质量单元。

图1 钻柱有限元模型

1.3.2 设定模型参数

钻柱材料弹性模量2.1×1011Pa，密度7800 kg／m3，泊松比0.3，钻井液密度1200kg／m3，重力加速度9.8m／s2，钻头承受钻压45×103N，井架和钢丝绳的综合刚度9.8×106N／m，地面系统质量6000kg。

1.3.3 设定固液耦合分析边界条件

确定柔性多体钻柱扭转振动时的边界条件为：①约束钻柱除绕轴旋转以外的所有自由度；②略去钻柱的横向振动和纵向振动，只提取钻柱扭转振动的前10阶固有模态进行分析。

2 固液耦合工况下钻柱扭振固有频率分析

2.1 钻井液对钻柱各阶扭振频率的影响

基于PIPE59、PIPE16两种单元特点，建立了2种不同的模型，即考虑井筒内钻井液影响和不考虑钻井液影响的模型。同时考虑钻柱自重及钻头静钻压等轴向载荷对柔性多体钻柱扭振频率的影响。得到钻柱扭转振动各阶固有频率，如表1所示。

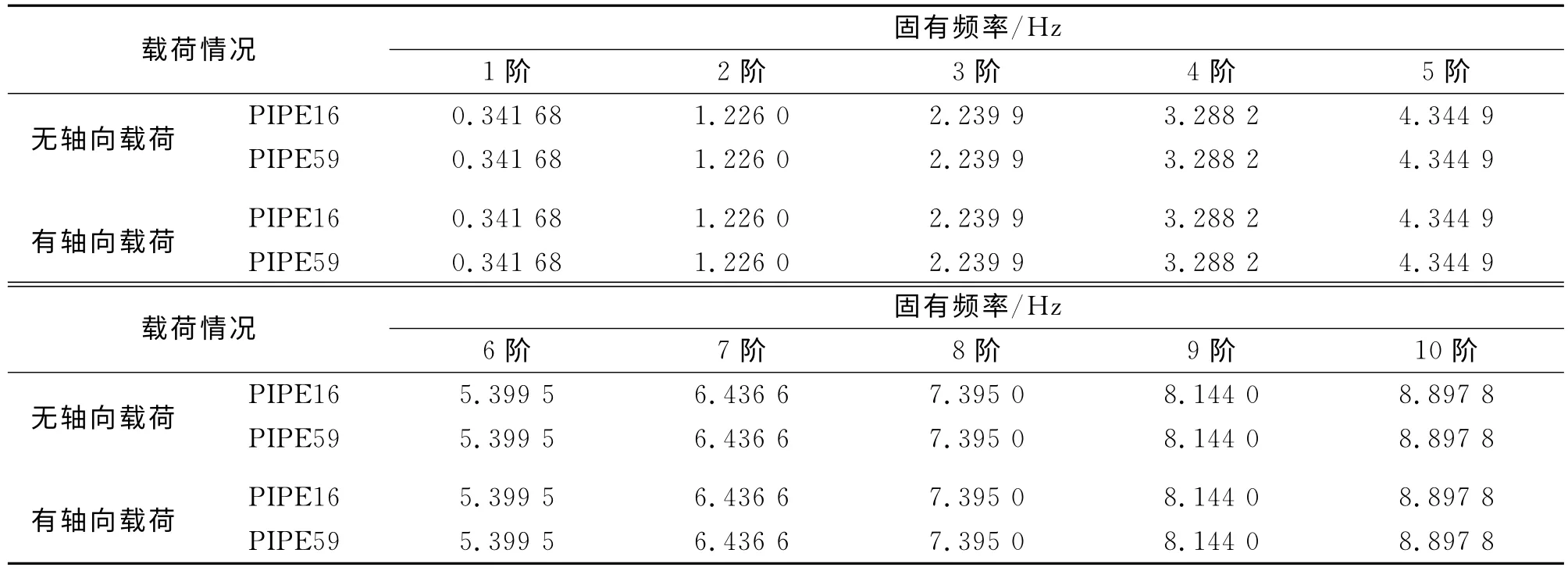
表1 1700m 钻井深度（钻铤200m＋钻柱1500m）钻柱扭振各阶固有频率

由表1可见：井筒中钻井液、轴向载荷等因素对钻柱的扭转振动没有影响，因此在分析钻柱的扭振频率时可以忽略井筒中钻井液、轴向载荷等因素的影响，使分析模型得到了简化，降低了工作量，节约了计算成本。下面的分析中不考虑钻井液等因素。

2.2 钻铤长度对钻柱各阶扭振频率的影响

以基于PIPE59单元建立的考虑井筒内钻井液影响的1700m 钻柱长度模型为例，钻铤长度以40 m为间隔，即80、120、160、200m。按此规律进行分析，得到了不同钻铤长度下钻柱的扭振频率，如表2所示。

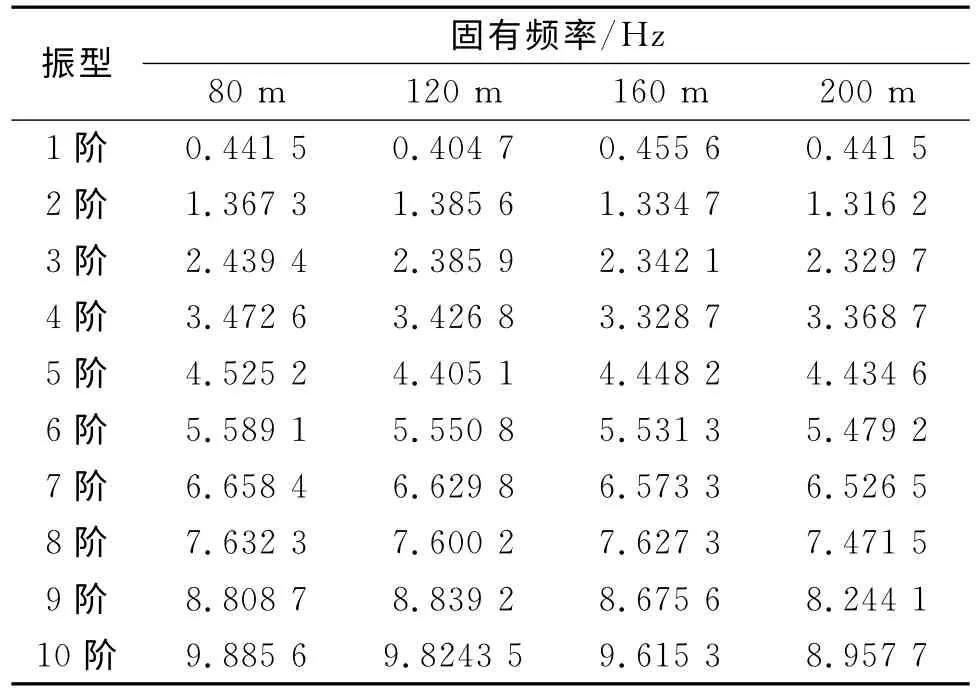
表2 不同钻铤长度下钻柱扭振各阶固有频率（1700m 钻柱）

为直观反应井下钻铤长度变化对钻柱扭振频率的影响，将表2中数据通过曲线图的方式表达出来，如图2所示。

钻柱的各阶扭振频率随钻铤长度的增加而减小，低阶固有频率减小慢，高阶固有频率减小快。当钻铤长度超过160 m 时，9阶、10阶扭振频率迅速下降。但是从总体上看来，钻柱扭转振动各阶固有频率随钻铤长度增加变化不大。

图2 钻柱扭振固有频率随钻铤长度变化曲线

2.3 钻柱长度对钻柱各阶扭振频率的影响

基于PIPE59单元建立的130m 钻铤长度模型为例，钻柱长度以200 m为间隔，即300、500、700、900、1100、1300、1500、1700m，得到了不同钻柱长度下钻柱的各阶扭振频率，如表3所示。

表3 不同钻柱长度下钻柱扭振各阶固有频率（130m 钻铤）

为了便于直观地反应井下钻柱长度变化对钻柱扭振频率的影响，特将表3中的数据通过曲线图的方式表达出来，如图3。

由图3可见：钻柱的扭转振动各阶固有频率随着钻柱长度的增加而减小，最后趋于不同的稳定值。由图2～3可见：钻铤长度变化对钻柱扭转振动各阶固有频率的影响远小于钻柱长度变化对钻柱扭转振动各阶固有频率的影响。总体而言，长度小于160m的钻铤长度变化对钻柱各阶扭转振动各阶固有频率的影响可以忽略。

图3 钻柱扭振固有频率随钻杆长度变化曲线

2.4 钻柱各阶扭转振动固有振型分析

以基于PIPE59单元特性建立的柔性多体钻柱模型为例，考察钻柱扭转振动的各阶固有振型，同样只提取前5阶固有振型进行分析。本模型钻柱长度1700m，钻铤长度200m。

为了考察钻柱扭转振动各阶固有振型的位移随钻柱距井口长度的变化规律，将钻柱扭转振动各阶固有振型的结果数据从ANSYS中提取出来，绘制成如图4所示曲线，图中的角位移单位为（°）。

由图4可见：钻柱各阶扭转振动固有振型的位移值在钻柱与钻铤接头处不是光滑连续的，有折角；钻铤上的位移随钻柱距井口长度的增加变化不大。图4直观地表示了钻柱前5阶扭转振动固有振型的位移沿钻柱距井口长度变化的分布及最大值，这对分析钻柱扭转振动时的受力，了解扭转振动的具体过程，采取合理的减振措施等方面提供了指导。

图4 1700m 钻柱各阶扭振固有振型曲线

3 结论

1）井筒中钻井液、轴向载荷等因素对钻柱的扭转振动没有影响，因此在分析钻柱的扭振频率时可以对此忽略，使分析模型得到简化，降低计算工作量。

2）随着钻铤长度的增加，钻柱的各阶扭振频率随之减小，低阶固有频率减小慢，高阶固有频率减小快。

3）随着钻柱长度的增加，钻柱的扭转振动各阶固有频率都随之减小，最后趋于稳定值。

4）钻铤长度变化对钻柱扭转振动各阶固有频率的影响远小于钻柱长度变化对钻柱扭转振动各阶固有频率的影响。总体而言，长度小于160m的钻铤其长度变化对钻柱扭转振动的各阶固有频率的影响可以忽略。

［1］韩致信，李钫，杨莉玲，等.钻柱纵向自由振动研究［J］.甘肃工业大学学报，2002，28（2）：50－53.

［2］刘清友，马德坤，汤小文.钻柱纵向振动模型的建立及求解方法［J］.西南石油学院学报，1998，20（4）：55－58.

［3］朱焕刚，张宝，张慢来.基于ANSYS软件的钻柱纵向振动分析［J］.石油矿场机械，2008，37（10）：56－58.

［4］江进国，舒晓勇，韦念龙，等.基于ANSYS软件的钻柱扭转振动分析［J］.探矿工程，2003（增刊）：176－178.

［5］Dareing D W.Drillstring vibrations create crooked holes［J］.Oil ＆Gas Journal，1984，82（1）：77－83.

［6］Mark W D.Nonlinear Drill String Dynamics.Ph D Dissertation，The University of Tulsa：1996Jansen J D.Non－linear rotor dynamics as applied to oilwell drill string vibrations［J］.Journal of Sound and Vibration，1991，（1）：115－135.

［7］刘清友，马德坤，钟青.钻柱扭转振动模型的建立及求解［J］.石油学报，2000，21（2）：78－82.

［8］于桂杰，殷有财，肖文生.顶驱钻井柔性钻柱动力学特性分析［J］.石油矿场机械，2011，40（4）：1－5.

［9］李子丰，张永贵.钻柱纵向和扭转振动分析［J］.工程力学，2004，21（6）：203－210.

［10］江进国.基于ANSYS软件的钻杆扭转振动分析［J］.探矿工程，2003（增刊）：176－178.

［11］赵国珍，龚伟安.钻井力学基础［M］.北京：石油工业出版社，1988.

［12］于永南.钻柱力学分析的有限单元法［M］.东营：石油大学出版社，1998.