基于应力刚化效应的直井钻柱横向振动分析

王 伟，但斌斌，容芷君，陈 刚，牛清勇，杨春雷

(1.武汉科技大学冶金装备及其控制教育部重点实验室，湖北 武汉，430081；2.武汉科技大学机械传动与制造工程湖北省重点实验室，湖北 武汉，430081；3.宝钢股份中央研究院武汉分院(武钢有限技术中心)，湖北 武汉，430080；4.中石化江钻石油机械有限公司，湖北 武汉，430223)

钻柱是钻井设备的核心部件，其受地面设备驱动，在充满液体或气体的狭长井眼中转动，带动钻头破碎井底岩石并形成井筒。钻柱在井眼中的运动状态是钻柱、钻井液与井壁或井底相互作用的结果。在钻井过程中，每段钻柱都有各自的固有振动频率，当钻柱受迫振动频率与钻柱固有振动频率重合时就会发生共振[1]。钻柱失效除了因为钻具本身的质量问题之外，还有一个重要原因是钻柱振动导致的钻具疲劳失效[2]，而钻柱的横向振动是导致钻柱磨损和疲劳破坏的主要因素。钻柱的横向振动一直是相关领域的研究热点。Heisig等[3]考虑了钻柱与井壁的碰撞影响，推导出钻柱的横向振动模型，研究了钻柱与井壁接触的振动规律，并计算了钻柱横向振动固有频率。韩春杰等[4]在考虑轴向动态载荷和静态载荷的情况下分析了受激状态下钻柱的横向振动规律。韩春杰等[5]还利用有限元软件研究了水平井钻柱横向振动，得出钻柱横向振动的频率分布规律。王宝金等[6]考虑到钻井液和钻柱的耦合作用，建立了水平钻柱横向振动数学模型。邓昌松等[7]利用单根钻杆模型分析了其在不同工况下的振动特性，得到横向振动的振型和应力-应变图。Ritto等[8-9]基于非线性Timoshenko梁理论建立了钻柱动力学非线性有限元方程。陈乐平[10]利用同伦分析法求解钻柱横向非线性振动方程，得到了非线性振动的频率和主振动的一阶近似解。李国庆等[11]考虑钻柱的纵向振动、横向振动、扭转振动之间的耦合关系，研究了钻柱振动的固有频率及振型。

目前基于有限元分析的钻柱动力学模型大致分为两种，即整体钻柱模型和底部钻具模型，模型的选取对钻柱振动分析十分重要。钻柱振动往往与钻柱的整体长度和结构形状密切相关，而上述研究大多没有从钻柱整体角度全面考虑轴向力对钻柱横向振动的影响。轴向力对钻柱横向振动的影响实质上是应力刚化效应的作用，因此本文根据几何非线性问题中的有限变形理论建立基于应力刚化效应的钻柱动力学方程，通过有限元仿真对比分析整体钻柱和底部钻具的横向振动差异，并选择合适的研究对象分析轴向力的应力刚化效应对钻柱模态、谐响应和瞬态响应的影响。

1 钻柱动力学模型的建立

1.1 不考虑应力刚化效应的钻柱动力学方程

建立钻柱动力学模型时根据实际情况作如下假设：由于井筒中柔性钻柱很长，假定钻柱处于线弹性变形状态；不考虑钻柱的纵向振动和扭转振动；忽略轴向移动、温度变化、钻井液浮力的影响；忽略钻柱和井壁碰撞产生的多支点，钻柱未发生螺旋扭曲；钻柱轴线与井筒轴线重合；钻柱上端固定，钻柱下端滚动铰支。钻柱简化模型如图1所示。

图1 钻柱简化模型Fig.1 Simplified drill string model

在有限元计算中，钻柱通常采用梁或管单元进行离散。三维管单元是空间上的一维线单元，每个单元包含2个节点，每个节点具有6个自由度，即有6个广义位移和6个广义力[12]。将钻柱沿着z轴方向离散为若干管单元，任取一单元，以单元轴线为oz轴，ox、oy为截面主惯性轴，如图2所示。

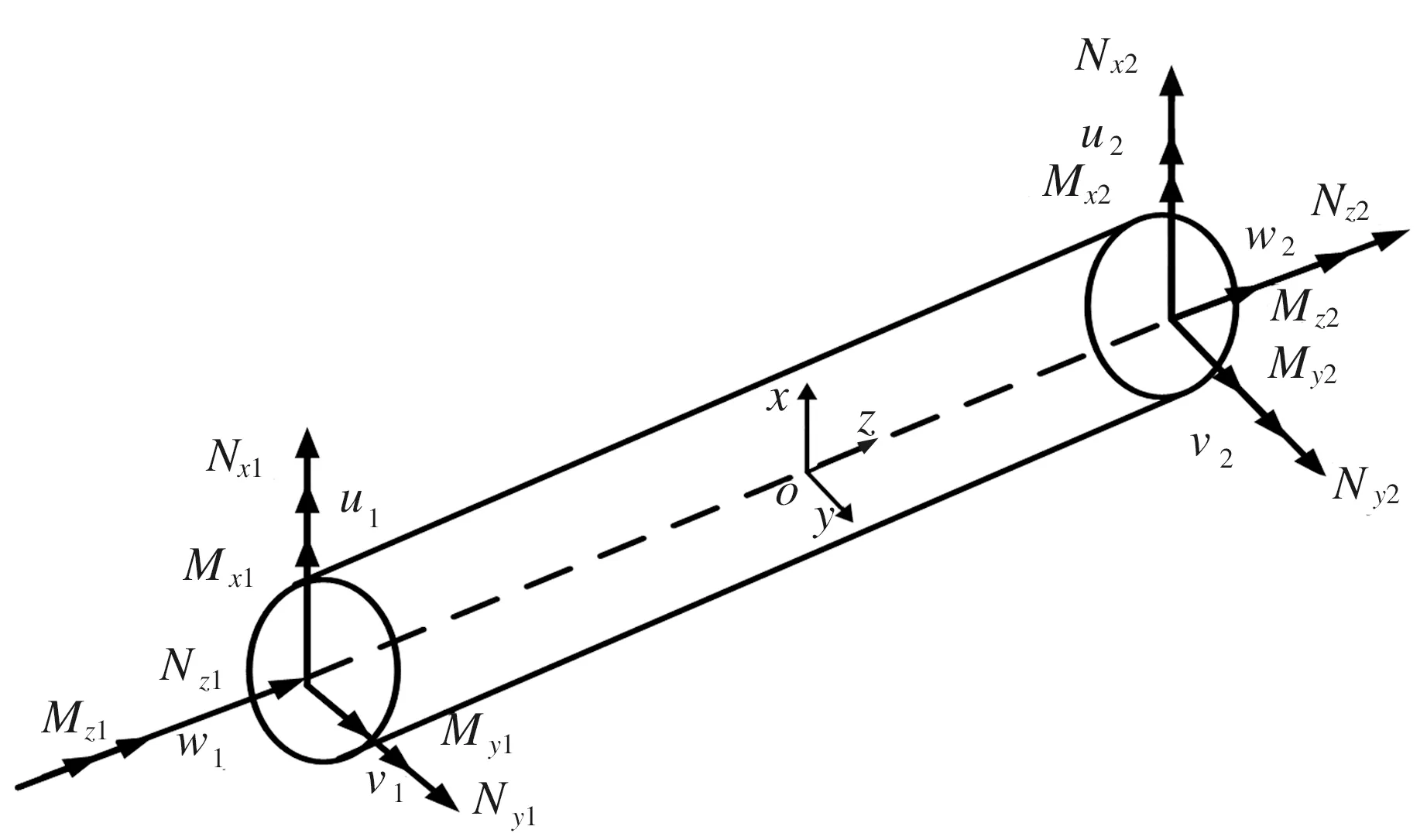
图2 钻柱单元受力与变形示意图Fig.2 Schematic diagram of force and deformation of drill string element

单元节点位移矩阵为

xe=(x1x2)T

(1)

其中xi=(uiviwiθxiθyiθzi)Τ,i=1,2。

单元节点力矩阵为

Re=(R1R2)Τ

(2)

其中Ri=[NxiNyiNziMxiMyiMzi]Τ,i=1,2。

上式中:ui、vi、wi分别为节点i在局部坐标系中三个方向的线位移；θxi、θyi、θzi分别为节点i处横截面绕三个坐标轴的转动角位移；Nxi为节点i的轴向力；Nyi、Nzi分别为节点i在xy、xz坐标面的剪力；Mxi为节点i处横截面上的转矩；Myi、Mzi分别为节点i在xz、xy坐标面内的弯矩。

考虑单元总能量和耗散函数，整理得到微元段在随体坐标系下的单元运动方程为

(3)

大地坐标(x,y,z)和随体坐标(X,Y,Z)之间的转换关系为

(4)

式中：α为大地坐标系绕x轴的旋转角度；θ为大地坐标系绕z轴的旋转角度。

坐标转换后，全井钻柱系统动力学方程可表示为

(5)

1.2 考虑应力刚化效应的钻柱动力学方程

在实际钻进作业中，钻柱自重大，且其下部会受到岩层的轴向反作用力。直井钻柱轴向力对钻柱产生的应力会直接影响钻柱的横向刚度，即产生应力刚化效应。应力刚化效应可以用考虑初应力刚度的有限元方法来实现，因此本文将初应力刚度矩阵添加到结构的弹性刚度矩阵中，形成考虑应力刚化后的切线刚度矩阵：

(6)

考虑应力刚化效应的全井钻柱系统运动学方程则可表示为

(7)

当激励矢量R(t)=0时，可对钻柱进行模态分析；当激励矢量R(t)为简谐载荷时，可对钻柱进行谐响应分析；当激励矢量R(t)为任意的随时间变化的载荷结构时，可对钻柱进行瞬态动力学分析。

2 钻柱横向振动仿真分析

2.1 有限元模型的建立

以一个全长1580 m的直井为例，所用钻井工具主要由钻杆和底部钻具构成。钻杆段包括普通钻杆和加重钻杆，底部钻具则包括钻铤、稳定器、钻头及井下特殊工具。

为了方便研究整体钻柱的横向振动特性，将复杂的钻具组合简化成钻杆部和钻铤部，形成变截面管模型。钻柱参数具体如表1所示。

表1 钻柱参数Table 1 Drill string parameters

在实际工况中，钻柱是管状结构，承受拉伸、压缩、弯曲和扭转的共同作用，同时会受到管内及管外流体的力学影响。在有限元分析中，Pipe59单元为单轴三维弹性直管单元，其在每个节点上拥有6个自由度，即分别沿着坐标轴x、y、z方向上的平移自由度和分别绕着这3个轴的旋转自由度，适用于考虑应力刚化和大变形的建模场景，因此本文采用Pipe59单元模拟钻柱系统在轴向力的应力刚化作用下的横向振动情况。

考虑到1500 m长的钻杆和80 m长的钻铤都是等截面管，形状简单，因此采用直接建模的方法建立钻柱有限元模型，即先生成节点，再通过节点生成单元，最后进行网格划分，得到钻柱有限元模型如图3所示。

图3 钻柱有限元模型

整体钻柱模型的总长为1580 m(1500 m钻杆+80 m钻铤)。建立底部钻具模型时，钻杆长度由1500 m缩短为150 m，钻铤长度仍为80 m，故底部钻具模型总长为230 m。分别对整体钻柱和底部钻具进行仿真分析。

2.2 整体钻柱和底部钻具的横向振动模态差异

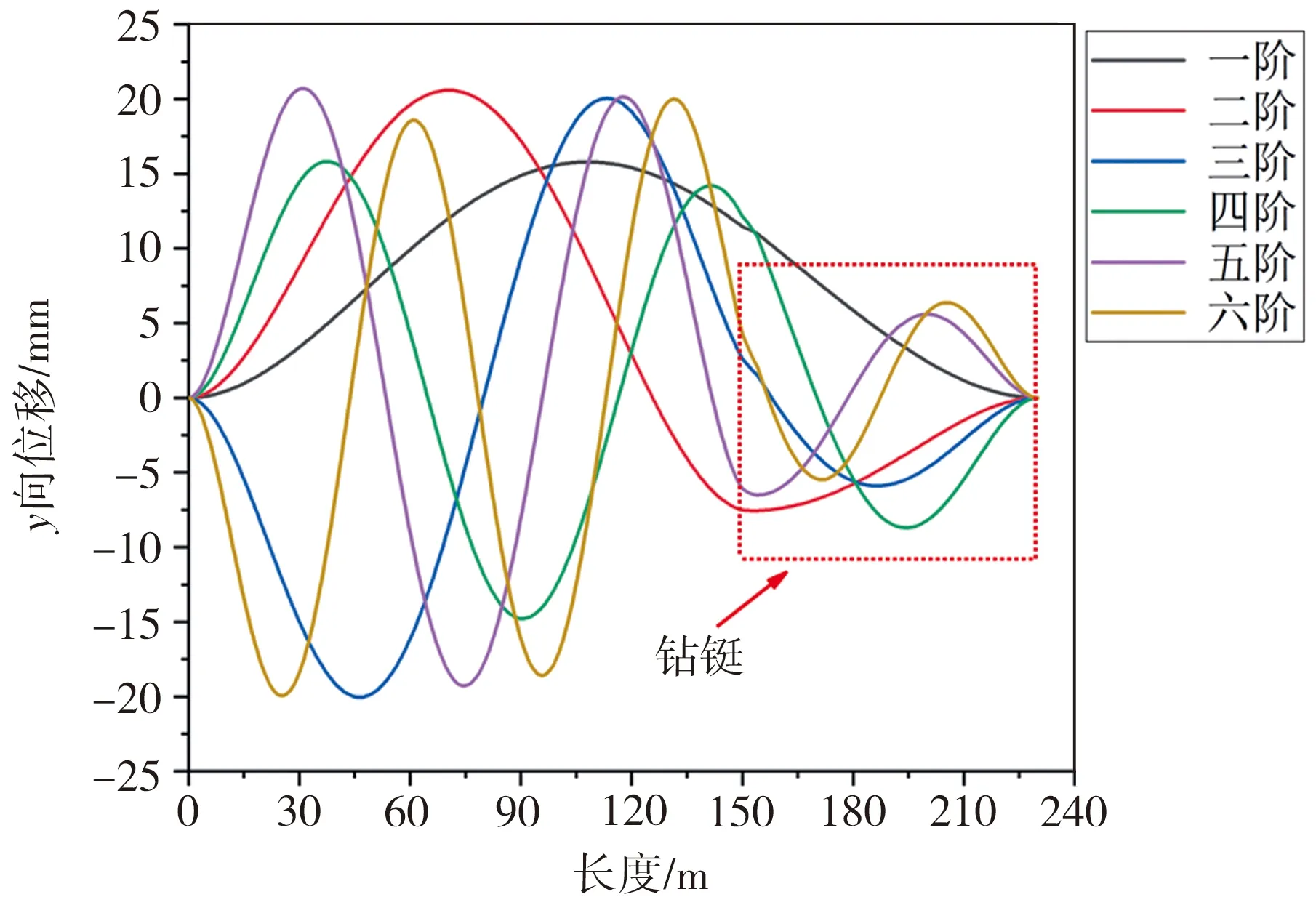
将钻柱水平放置，在不考虑应力刚化效应的情况下分析整体钻柱和底部钻具横向振动模态的差异。边界条件为：钻柱顶端设置为固定端，钻柱下端设置滚动铰支，限制轴向移动和扭转，只考虑钻柱的横向振动。利用Block Lanczos法提取前10阶横向振动固有频率和前6阶振型，由于x-z方向和x-y方向振动相同，因此只提取x-z方向上的频率和振型。整体钻柱和底部钻具的前10阶横向振动固有频率如图4所示，整体钻柱和底部钻具的前6阶振型如图5所示。

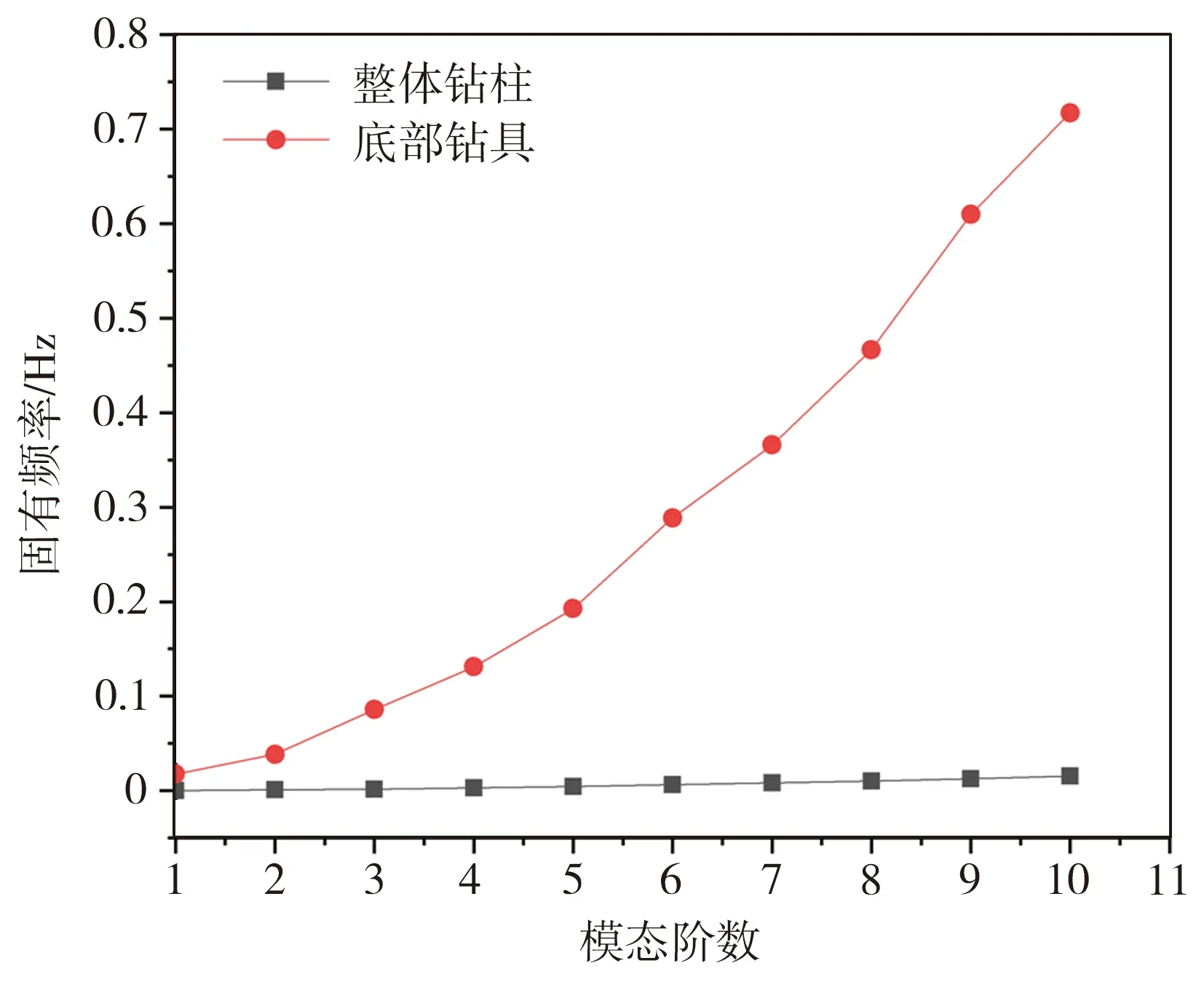
图4 整体钻柱与底部钻具的横向振动固有频率Fig.4 Inherent frequencies of transverse vibration of the whole drill string and the bottom drill

(a)底部钻具

从图4可以看出，整体钻柱和底部钻具的横向振动固有频率相差很大，前者普遍较低。整体钻柱和底部钻具的低阶固有频率较为接近，阶数越高，整体钻柱固有频率低于底部钻具固有频率的幅度越大，这表明整体钻柱大部分发生的是低频横向振动，而且相邻阶的频率差距非常小，因此共振区较宽，钻柱整体横向振动很难避免。

从图5可以看出，整体钻柱与底部钻具的振型基本相同，但在钻铤部有较大差异，整体钻柱钻铤部位的位移明显小于底部钻具钻铤部位的位移，表明不考虑自重和钻压产生的轴向力时，钻杆长度会影响钻铤的横向振动。这主要是因为钻杆越长，钻杆与钻铤的刚度差距越大，钻铤振动越不明显。

模态阶数越低，模态有效质量越大，在钻进时越容易被激励而引起振动，因此需要格外关注钻柱的低阶振动。建立钻柱局部力学模型时通常只截取底部钻具作为研究对象。与整体钻柱相比，底部钻具的刚度大得多，造成钻柱的横向固有频率过大，其低阶振动容易被忽视，导致整体钻柱的低阶固有频率和固有振型丢失。由此可见，分析钻柱的横向振动时，整体钻柱模型可以更准确地反映钻柱的低阶固有频率和振型，更符合钻柱的实际振动状态。

2.3 轴向力对整体钻柱横向振动模态的影响

鉴于整体钻柱模型的优势，以下分析都是以整体钻柱作为研究对象。整体钻柱受到的轴向力主要包括整体自重产生的拉力以及钻压引起的轴向压力，在有限元计算中只要给出钻柱轴向的重力加速度就可以确定自重产生的拉力。用考虑初应力刚度的有限元法对整体钻柱进行轴向力影响下的模态分析，由于研究的是不发生弯曲的竖直钻柱，为保证钻柱竖直钻进的稳定性，设置的钻压应小于钻铤重力。经计算，钻铤重力为125.552 kN，钻压范围为0～125.552 kN，钻压分别取值0、50、100 kN，分析重力和钻压对钻柱横向振动固有频率的影响，结果如图6所示。为考虑轴向力对钻柱振型的影响，提取重力和50 kN钻压作用下的振型，如图7所示。

从图6可以看出：轴向力对整体钻柱横向振动固有频率的影响很大；自重会显著提高钻柱的横向振动频率；随着钻压的提高，钻柱的横向振动固有频率不断下降，但还是远高于无轴向力时的频率值，这是因为钻压与自重相比过小，钻柱总体还是受拉应力，在应力刚化的作用下，钻柱横向振动固有频率大幅提高。

图6 不同轴向力下整体钻柱的横向振动固有频率Fig.6 Inherent frequencies of transverse vibration of the whole drill string subjected to different axial forces

一般认为，钻柱中性点附近的横向振动最为剧烈[13]，因此将中性点作为评价钻柱横向振动的参考点。根据钻压和钻铤的单位质量可以计算出中性点的位置离井底26.8 m，即图7中A点(横坐标为1553.2 m)所示。从图7可以看出，靠近中性点附近的钻柱振幅最大，同时钻杆与钻铤连接处振型有偏折现象，因此需要加重钻杆进行过渡，避免过大的交变应力；另外，钻杆部分从靠近中性点处到井口处的振幅不断降低，对比图5(b)可知，轴向力不仅会影响钻柱的横向振动振型，也是钻柱横向振动从井底到井口逐渐减弱的原因之一。

图7 重力和50 kN钻压下的整体钻柱横向振动振型Fig.7 Transverse vibration modes of the whole drill string subjected to gravity and 50 kN drill pressure

2.4 钻柱的预应力谐响应分析

钻柱在工作过程中会受到稳定器的作用，从图7中找到前几阶振型中最大振幅出现的位置(如图7中B点所示)安装稳定器，选取该位置为谐响应激振力作用点。考虑不同预应力的作用，设置自重及钻压(0、50、100 kN)，采用模态叠加法进行预应力谐响应分析。考虑钻柱转速处于低档区(0～90 r/min)，所以谐响应频率范围定为0～1.5 Hz。给钻柱施加10 kN径向激励载荷，以中性点为整体钻柱的重要考察点，研究钻柱在激励载荷作用下的振动响应，结果如图8所示。

为了研究预应力下的钻柱谐响应特点，下面重点分析在自重和50 kN钻压作用下的仿真结果。从图8(b)可以看出，钻柱横向振动的共振区很宽，中性点的横向位移响应曲线波动剧烈，在0～1.5 Hz范围内发生了多次位移突变，尤其在0.15、0.65、1.15 Hz时的位移变化更加剧烈，响应幅值很大，最大振幅为5.3 mm。上述3个频率值对应的转速分别为9、39、69 r/min，均处于钻机正常工作转速范围之内。当激励频率为0.4～0.6 Hz(对应的转速为24～36 r/min)时，位移响应幅值明显小于其余频段响应幅值，即存在共振微弱区。共振时钻柱位移过大，钻柱会与井壁碰撞，造成井壁损坏，并且钻柱的交变应力增大，容易疲劳失效，因此钻柱工作时应避开危险共振区，当无法避免时要尽量选取共振微弱区。

(a)钻压为0

另外，由图8可知：钻压为0时，共振微弱区频率范围为0.45～0.7 Hz；钻压为50 kN时，共振微弱区频率范围为0.4～0.6 Hz；钻压为100 kN时，共振微弱区频率范围为0.3～0.5 Hz。也就是说，不同的钻压分别对应一个共振微弱区，而且钻压越大，共振微弱区越前移，因此，当钻压较大时，应选择较低的钻柱转速以避开危险共振区。

2.5 钻柱的预应力瞬态分析

钻柱工作时易与井壁发生碰撞，为了研究应力刚化对钻柱与井壁撞击时的钻柱瞬态响应的影响，将自重和50 kN钻压共同产生的轴向力作为预应力设置，分别进行有、无预应力下模态叠加的瞬态动力学分析。由图7可以看出，钻柱与井壁最可能发生碰撞的位置距井口1400 m左右，因此在此处设置碰撞载荷10 kN、碰撞时间为0.01 s，然后分析中性点处10 s内的动态响应。无预应力和有预应力时中性点处y方向的位移响应曲线和加速度响应曲线分别如图9和图10所示。

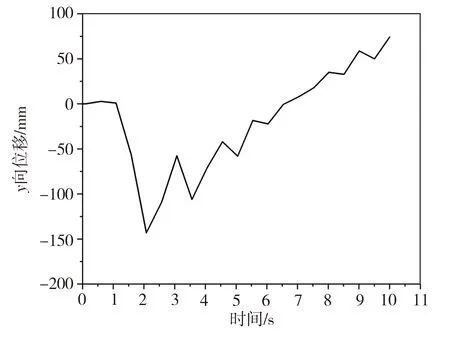
(a)无预应力

从图9可以看出：钻柱在井下1400 m处与井壁发生碰撞时，下部的中性点发生伴随振动；有预应力时，钻柱中性点最大振幅为55.2 mm；无预应力时，钻柱中性点最大振幅为142 mm。这是因为轴向力会显著提高钻柱的刚度，即产生应力刚化效应，钻柱抵抗变形的能力更强，不易发生较大的横向变形，从而降低了中性点与井壁发生碰撞的可能性。

(a)无预应力

由图10可以看出：无预应力时，钻柱与井壁碰撞后中性点的加速度较小，其变化范围为-0.9～0.823 m/s2；在钻压和钻柱自重产生的应力刚化作用下，中性点的横向加速度相对较大，在-1.4～2.132 m/s2之间波动，且加速度波动频率明显提高。这表明在预应力作用下，钻柱与井壁碰撞后中性点处的冲击载荷更大、振动更加剧烈且横向振动能量更大。

3 结论

(1)与底部钻具相比，整体钻柱的横向振动共振区较宽，同时频率大都很低，可以更准确地反映出钻柱的低频振动情况，故研究钻柱的横向振动时以整体钻柱作为研究对象更为适合。

(2)钻柱自重产生的轴向力会显著提高钻柱的横向振动固有频率，钻压会降低该频率，增大钻压会使钻柱的横向振动不断减弱。轴向力会改变钻柱的横向振动固有振型，同时导致钻杆部从中性点附近到井口的振幅不断降低，振动越来越弱。

(3)基于预应力的谐响应分析表明，钻压为50 kN、钻柱处于0～90 r/min的转速区段时，存在频率为0.4～0.6 Hz(对应转速为24～36 r/min)的共振微弱区，此时钻柱的振幅较小；钻压越大，共振微弱区对应的激励频率越低，因此当钻压较大时，应选择较低的转速避开共振危险区。

(4)基于预应力的瞬态动力学分析表明，在轴向力产生的应力刚化作用下，钻柱与井壁发生碰撞后产生的应力波使钻柱中性点处的振动能量增大但振幅降低，与不考虑预应力时相比，钻柱与井壁发生碰撞的可能性降低了。