基于液压机械臂的主动柔顺控制

罗建雄，赵 慧,2，蒋 林,2

(1.武汉科技大学冶金装备及其控制教育部重点实验室，湖北 武汉，430081;2.武汉科技大学机器人与智能系统研究院，湖北 武汉，430081)

随着机器人技术的不断发展，单纯的位置控制机械臂已经不能满足更高的性能要求。对于输出力矩较大的液压机械臂[1]，当它与外部环境发生碰撞接触时必须采用合理的柔顺控制策略[2-3]来保障人机物理接触安全，其中，被动柔顺控制[4]虽能降低碰撞瞬间冲击力和整个碰撞过程中的接触力，但它不能使机械臂逃离碰撞物并保持在一个安全状态，因此碰撞发生后还需辅以主动柔顺控制[5]以合理控制机械臂。

机器人的主动柔顺控制大致可分为直接法和间接法。直接法对机械臂力和位置进行直接控制，以Raibert等[6]于1981年提出的力-位混合控制方法为代表；间接法使机械臂力和位置之间形成一种动态关系，以Hogan[7]于1985年提出的阻抗控制为代表。因为阻抗控制的原理较简单并且鲁棒性强，所以目前机械臂的主动柔顺控制大多采用该方式。针对人机意外碰撞接触，De Luca等[8]和Haddadin等[9]基于DLR机械臂采用阻抗控制及其它反应策略进行了碰撞实验，结果表明，所用反应策略均能驱使机械臂逃离碰撞物使接触力快速减小。在采取主动力控制策略时，可将传统阻抗控制与自适应控制[10]、模糊控制[11]、神经网络控制[12]等结合来对机器人进行力控制，如Duan等[13]提出了一种自适应变阻抗方法，能对动态环境进行动态力的跟踪；武琦琦[14]提出利用变刚度参数和变阻尼参数的阻抗控制进行力跟踪；Dong等[15]提出了一种基于速度的变阻抗自适应交互控制方法，根据交互式力跟踪误差，自适应地调整导纳控制器的阻尼参数；Peng等[16]在力控制外环中将PID控制与阻抗控制结合，在位置控制内环中采用自适应Jacobian矩阵和RBFNN方法来补偿系统模型参数不确定性和动态不确定性，可以有效地跟踪所期望的接触力及位置轨迹。不过，已有研究对于人机物理接触后的力跟踪大多仅考虑了稳态时的跟踪精度，却忽略了动态接触时的力响应，造成机械臂与环境接触初始阶段的接触力产生超调和振荡，这可能会导致力控任务失败。因此，本文将PI控制器与阻抗控制结合以消除阻抗控制的稳态接触力误差，并借助递归最小二乘法来估计未知环境的参数，再根据所估计的环境参数及力误差对阻抗参数进行调节，使机械臂在与不同的未知环境进行力接触时都可以实现具有零稳态误差、低过冲及快速上升的力响应。

1 液压机械臂模型

1.1 液压转角自伺服柔顺关节结构

图1所示为液压转角自伺服柔顺关节结构，主要由阀套、阀芯、阀体、缸体、阀体轴承、阀体叶片、舵机等组成，其中由阀体和缸体组成的工作腔被叶片和固定挡块分成A、B两部分。该液压关节结构的基本工作原理为：高压油液经高压油嘴进入高压油通道，低压油回入回油嘴。当舵机停止时，阀芯处于中位，即阀芯上的矩形槽与阀套上的凸台封闭，高、低压油液不能经阀芯与阀套形成的配流口进入A、B工作腔。当阀芯顺时针转动一定角度时，高压油液经高压通道从阀体叶片径向方向流入P口，再经配流口及阀体矩形孔流入A腔,进而在两个工作腔的压差下推动阀体叶片顺时针旋转，并由阀体输出轴输出扭矩，此时，B腔容积开始压缩，其内部的低压油经过阀体矩形孔进入低压油通道。当阀芯逆时针旋转时，其工作状况与阀芯顺时针旋转时相反但原理相同。

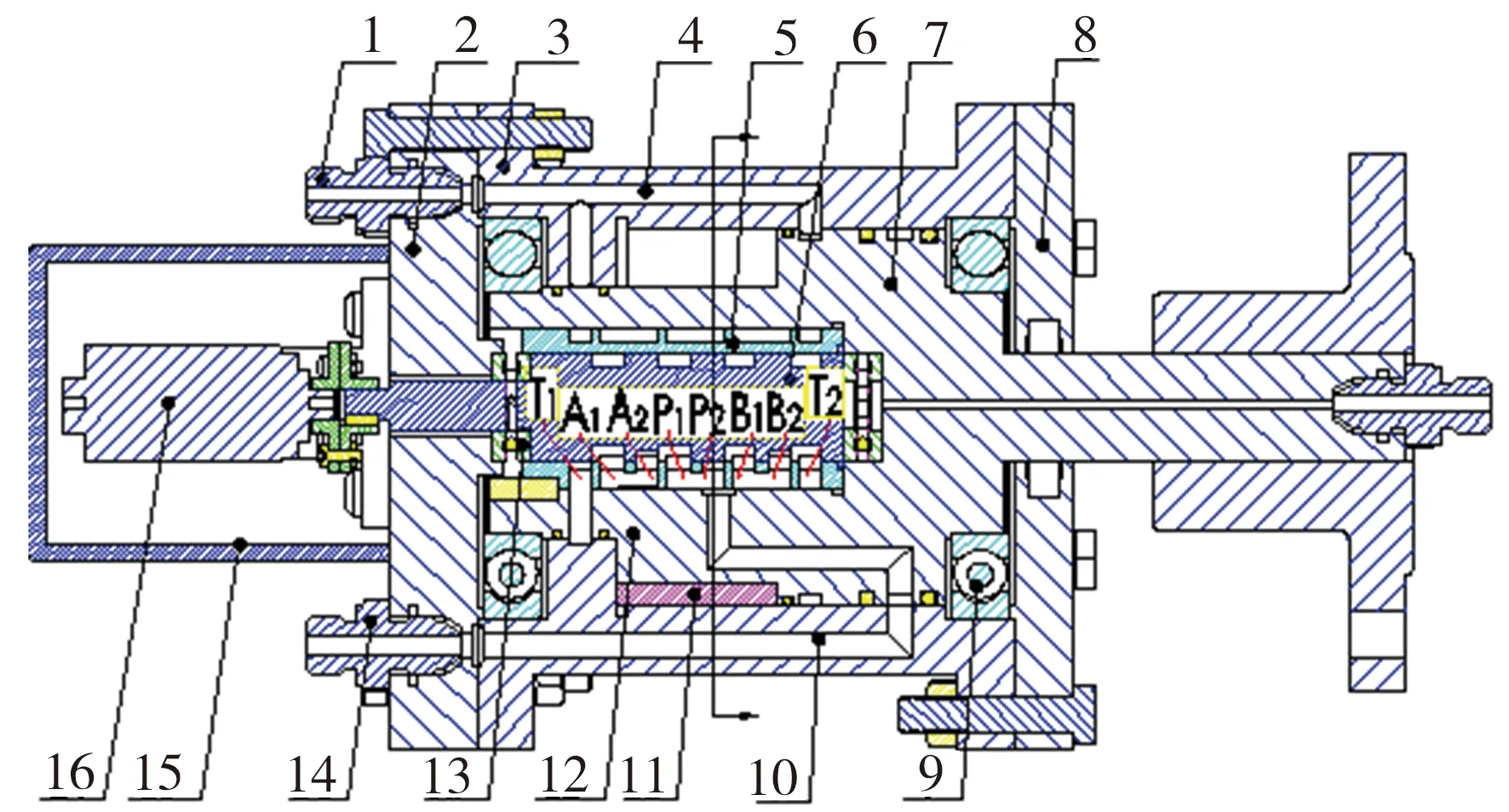
1—低压油嘴；2—左端盖；3—缸体；4—低压油通道；5—阀套；6—阀芯；7—阀体；8—右端盖；9—阀体轴承；10—高压油通道；11—叶片密封；12—阀体叶片；13—阀芯轴承；14—高压油嘴；15—罩子；16—舵机图1 液压转角自伺服柔顺关节示意图Fig.1 Schematic diagram of hydraulic angle self servo compliant joint

1.2 液压机械臂三维模型的构建

以图1所示的液压关节为驱动机构构建一个3自由度机械臂来进行相关的仿真模拟实验，其SolidWorks模型如图2所示。该模型主要由1个回转关节和2个摆动关节组成，其中回转关节安装在机械臂基座内，基座与大地固定。各关节之间通过连杆连接，模型末端为一个简化的执行器。

图2 机械臂结构Fig.2 Structure of manipulator

2 液压转角自伺服柔顺关节的动力学模型

2.1 阀口流量方程

图3所示为液压转角自伺服柔顺关节中阀口的几何关系。阀口形状为矩形，宽度为a，阀芯半径为r，阀口相对于阀芯轴线的圆心角为θ，设阀芯顺时针转过的角度为θ1，阀体顺时针转过的角度为θ2，当阀芯顺时针旋转时，开口面积A有以下几种变化情况：

图3 阀口几何关系图Fig.3 Geometric diagram of valve port

(1)

由液压系统流量平衡原理[17]可知，阀口负载流量qL的计算方程为：

(2)

式中，Cd为阀口流量系数，pS为系统供油压力，pL为负载压力，ρ为油液密度。

2.2 关节工作腔流量连续方程及负载力矩平衡方程

假定液压伺服被动柔顺关节连接管道中的压力损失和管道动态可以忽略，且液压关节所有工作腔内各处压力相等，在不考虑弹性负载影响的条件下，关节工作腔流量连续方程及阀体输出力矩与负载力矩的平衡方程分别为[18]：

(3)

(4)

式(3)～式(4)中，Dm为工作腔的角弧度排量，Ctp为工作腔总泄漏系数，Vt为工作腔及管道的总容积，βe为油液的体积弹性模量，Jt为关节和负载折算到配流轴上的总惯量，Bm为关节和负载的黏性阻尼力系数，TL为作用在输出轴上的任意外加负载力矩。

基于式(2)～式(4)等关节动力学模型，利用MATLAB/Simulink建立液压转角自伺服柔顺关节系统的仿真模型如图4所示，利用该液压关节模块所构建的机械臂运动模型见图5。

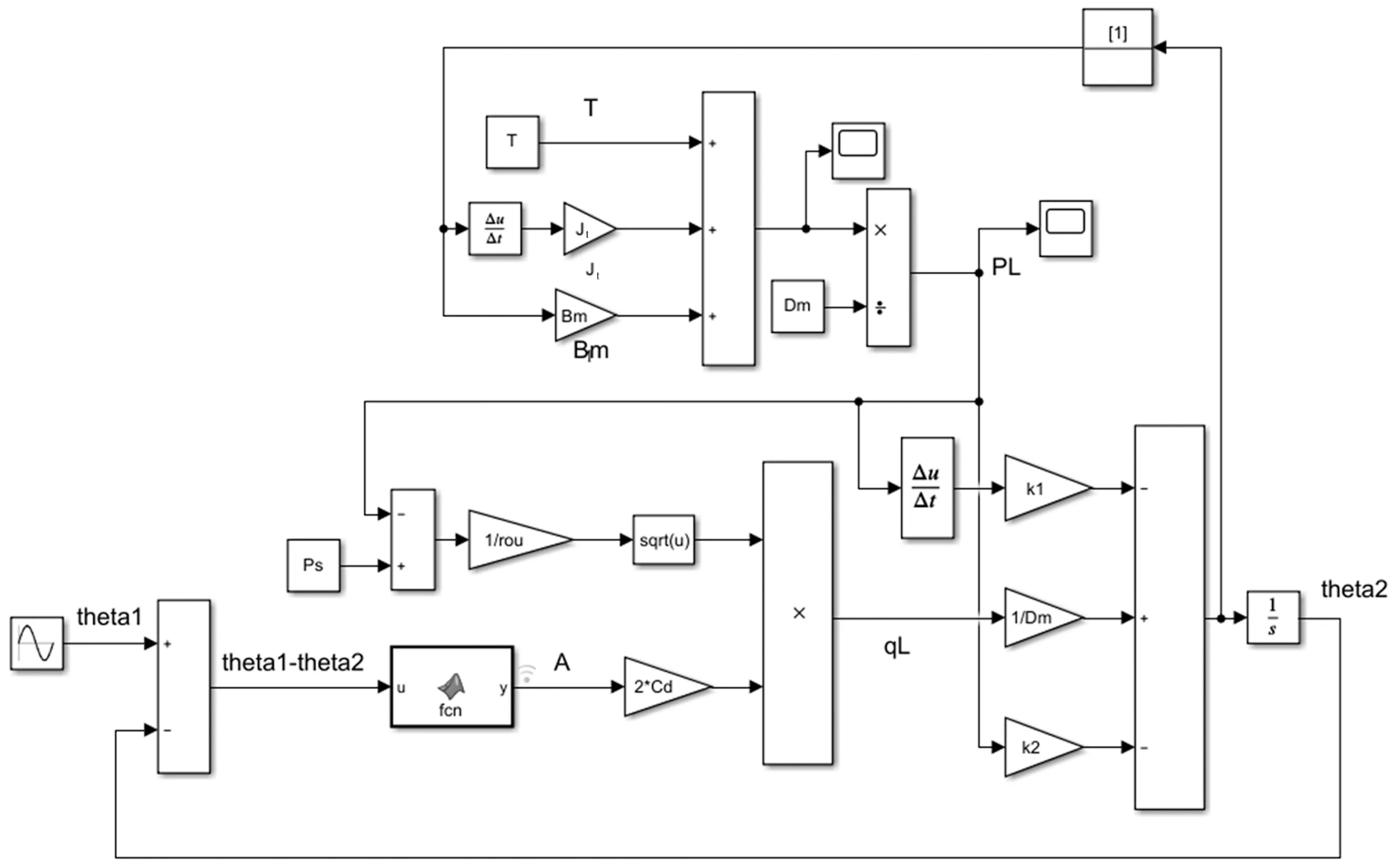
图4 液压关节仿真模型图Fig.4 Simulation model diagram of hydraulic joint

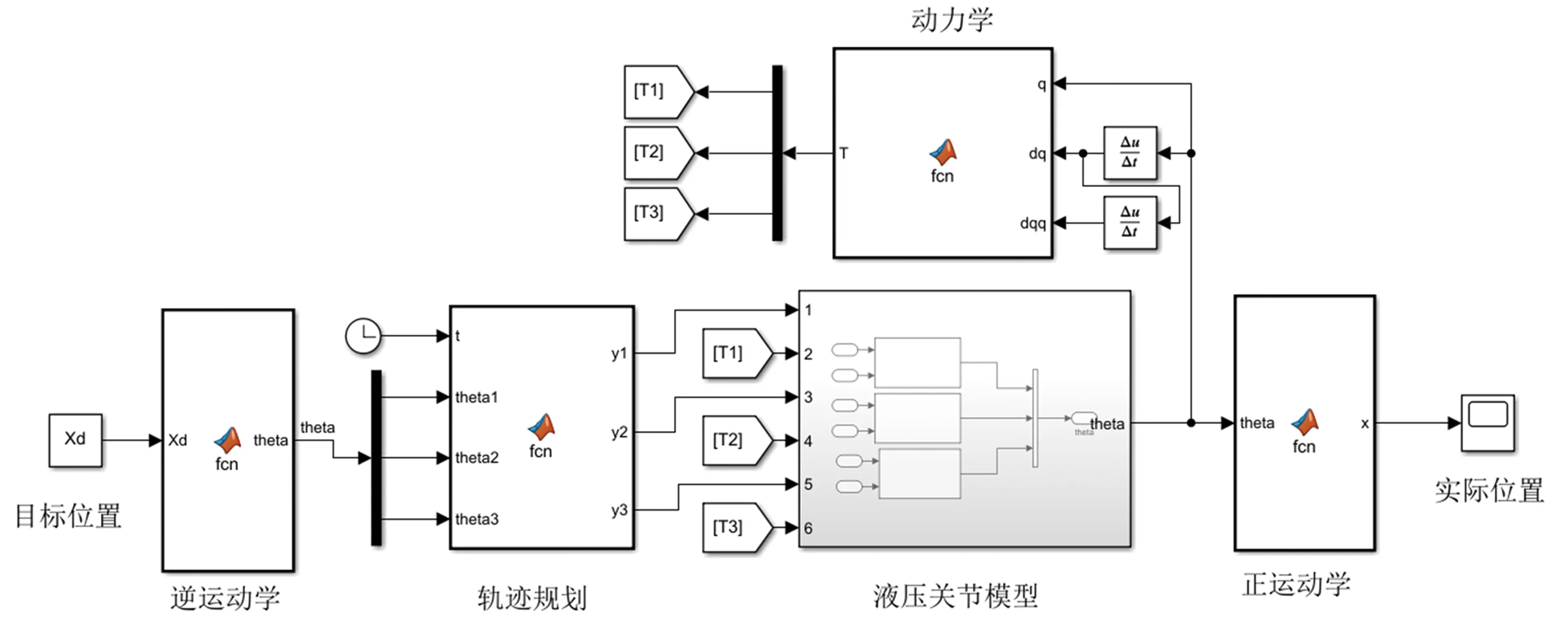
图5 液压机械臂的运动模型Fig.5 Motion model of hydraulic manipulator

3 意外碰撞及主动接触时的主动柔顺控制

3.1 意外碰撞时的主动柔顺控制

3.1.1 阻抗控制

阻抗控制可基于位置(即导纳控制)也可基于力，本研究采用导纳控制，其简要原理如图6所示。图中Xd、Xc和Xm分别表示参考位置轨迹、命令位置轨迹及测量位置轨迹，e为阻抗控制生成的位置修正量，假设机械臂的位置跟踪精度很高，即Xc=Xm，则e=Xc-Xd=Xm-Xd；Fd表示所需的期望接触力，Fe表示环境的实际接触力，则力跟踪误差ΔF=Fd-Fe。

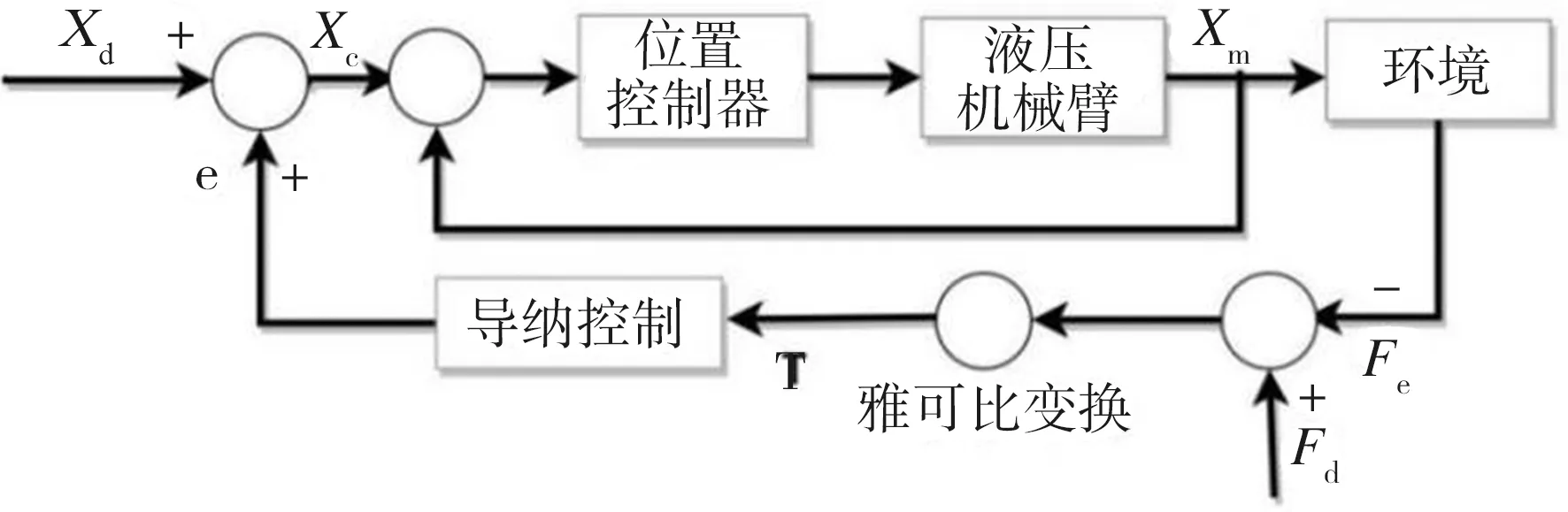
图6 基于位置的阻抗控制Fig.6 Position based impedance control

在图2所示的3自由度机械臂中，对3个关节均设计1个阻抗控制系统，阻抗控制模型为：

(5)

式中，J为Jacobian矩阵，M、B、K分别是机械臂阻抗质量参数、阻尼参数及刚度系数，皆为3×3的对角矩阵；T1、T2、T3分别表示3个关节上的作用力矩，e1、e2、e3分别表示3个关节的角度修正量。当机械臂与外界发生意外碰撞且传感器检测到碰撞力Fe时,利用Jacobian矩阵将力误差等效为各关节的作用力矩T，然后将T输入对应关节的阻抗控制系统从而得到关节的角度修正量e，再将关节角度修正量传给舵机，通过控制舵机来改变液压关节的输出角度，从而使机械臂与外界处于力-位置的动态控制之下。

3.1.2 速度控制

速度控制是一种比较简单的反应控制策略，当机械臂与外界发生意外碰撞时，先将检测到的碰撞力用Jacobian矩阵转化为各关节的等效作用力矩，再将碰撞力通过相关运算转化为速度矢量，最后将速度矢量传输给机械臂控制系统以驱使机械臂逃离碰撞。速度控制模型为：

(6)

3.1.3 意外碰撞仿真实验

当检测到意外碰撞发生时，机械臂应立刻激活安全控制策略以保障人机接触安全。为此，意外碰撞仿真实验以机械臂无控制策略作为对照组，分别使用阻抗控制(策略1)及速度控制(策略2)两种策略来处理意外碰撞，其中，在采取阻抗控制策略时，设置期望接触力Fd为0，M=diag[1;1;1],B=diag[100;100;100],K=diag[20;20;20],C取0.05，相应的仿真实验结果如图7所示。由图7可见，在不采用控制策略条件下，机械臂与外部环境发生意外碰撞接触后继续向目标位置前进，随着来自环境的阻力不断增大，机械臂与环境之间的接触力也不断增大；在采用阻抗控制策略条件下，当机械臂与外部环境发生接触后，该控制机制立即产生一个位置修正反馈以驱使机械臂逃离碰撞，最终机械臂和外部环境之间维持一个较小的稳定接触力；在采用速度控制策略条件下，当意外碰撞发生时，机械臂与外部环境之间的接触力触发速度控制机制，使得机械臂可以快速地远离接触力源，直至接触力衰减为0后停止运行。由此可见，在意外碰撞发生时，采用阻抗控制策略或速度控制策略都能使机械臂快速逃离碰撞物以降低碰撞作用力。从图7中还注意到，虽然采用阻抗控制策略或速度控制策略都能降低机械臂与外部环境之间的碰撞力，但由于阻抗控制策略本身的局限性，最终机械臂与外部环境之间的接触力不为0，没有达到所设置的接触力期望值，故而需要在对力误差产生原因进行分析的基础上进一步改进阻抗控制策略。

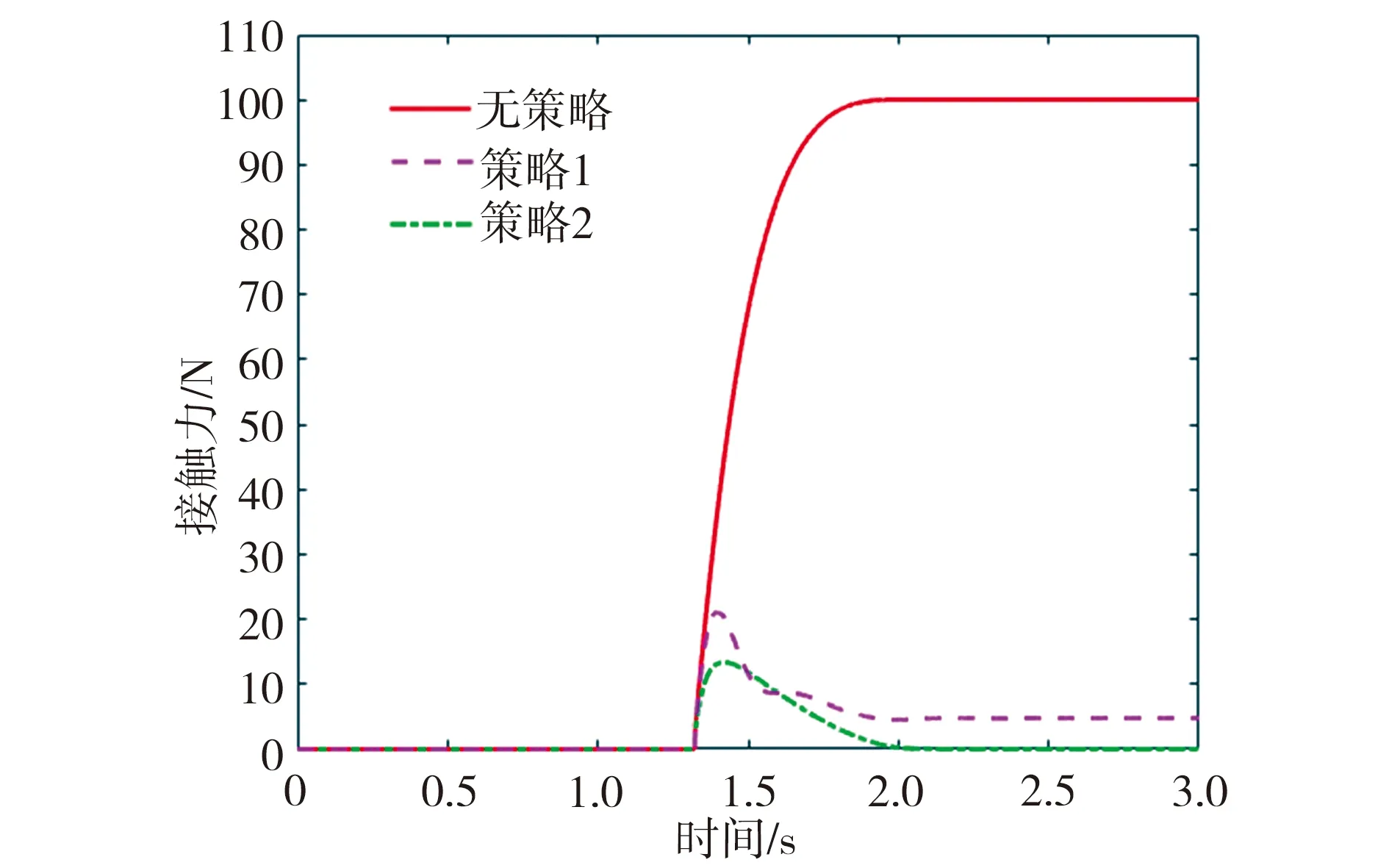
图7 不同控制策略时的仿真结果Fig.7 Simulation results under different control strategies

为了便于进行理论分析，将三维空间简化为一维空间，使用fd、fe、xc、m、b、k分别替换Fd、Fe、Xc、M、B、K，则力误差Δf为：

Δf=fd-fe=fd-ke(xc-xe)

(7)

式中，ke为环境刚度，xe为环境位置。机械臂的阻抗控制表达式为：

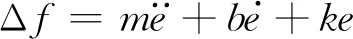
(8)

令阻抗系统传递函数为k(s),有：

(9)

关节的位置修正量e为：

e=k(s)Δf

(10)

机械臂末端位置为：

xc=xd+e

(11)

将式(10)～式(12)代入(7)中，则有：

Δf=fd-ke(xd+k(s)Δf-xe)

(12)

当系统处于稳态时，即k(s)=1/k，整理可得力误差表达式为：

(13)

当xd=xe+fd/ke时，力跟踪误差将在稳态下收敛为0，换言之，要使力误差收敛为0，必须确定外部环境的位置和刚度，但在意外碰撞发生时很难准确获取外部环境的位置和刚度信息，因此在式(8)等号左侧加入积分项以消除稳态误差，相当于引入力误差的PI控制器，其中比例系数kp取1，积分系数为kI，则有：

(14)

环境接触力表达式为：

fe=(xc-xe)ke

(15)

式中，xc=xd+e，当期望参考位置xd大于环境位置xe，机械臂与外部环境才会发生接触，因环境的位置未知的，令Δx=xd-xe，式(15)可改写为：

fe=(e+Δx)ke

(16)

将式(16)带入式(14)经微分得：

(17)

式(17)经拉氏变换整理得：

(18)

根据终值定理求解稳态时位置修正量，有：

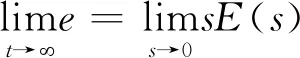
(19)

将式(19)带入式(16)求解得此时的接触力为：

(20)

计算结果表明，接触力与其期望值相等。基于上述改进的阻抗控制策略进行意外碰撞仿真实验的结果如图8所示。由图8可见，在采用阻抗控制策略处理意外碰撞时，将PI控制器与阻抗控制相结合可使最终接触力收敛到0，有效提高了机械臂稳态时的安全性。

图8 改进后的仿真结果Fig.8 Improved simulation results

3.2 主动接触时的主动柔顺控制

3.2.1 常阻尼阻抗控制

当机械臂执行某些特定任务需与外部环境发生主动接触时，后者位置一般是已知的，此时，可根据外部环境位置利用逆运动学求解出各关节的角度，将求解所得结果输入液压关节系统来驱使机械臂运动到外部环境表面，然后输入作用力期望值并借助Jacobian矩阵将其转换为关节等效力矩，输入至各关节的阻抗控制系统从而产生关节角度修正量以驱使机械臂与环境进行接触。在此，基于机械臂与外界进行力控任务时的一维模型进行相关分析，为了消除稳态力误差，仍将阻抗控制与PI控制器结合。当机械臂与外界环境接触时，通过传感器获取接触力值，并在稳态力误差分析中使用由式(15)计算所得值替代传感器所获接触力，在进行动态力跟踪时，还需加入阻尼项，则接触力近似值计算公式为：

(21)

式中，be为环境的阻尼。已知xc=xd+e，令期望位置xd=xe，代入式(21)，可得：

(22)

将式(22)带入阻抗控制模型，经整理得：

(23)

3.2.2 变阻尼阻抗控制

因阻抗控制阻尼值对力跟踪的动态过程影响很大，所以对于未知环境，采用常数阻尼参数的动态力跟踪效果是不确定的。为了确保机械臂在不同环境下都能较好地完成力接触任务，本研究从3个方面来改进阻抗控制，其控制原理见图9，具体措施为：

图9 变阻尼阻抗控制Fig.9 Variable damping impedance control

(1)设计一种能够防止在接触条件下接触力过冲的算法。选用力响应的一阶参考模型，模型参考力fm为：

(24)

式中，c为系统带宽参数，c越大，fm响应越快。

(2)根据力误差设计一种变阻尼阻抗控制。由于外部环境未知，为了避免接触力产生过大超调，阻尼系数初始取值较大，根据力误差调整阻尼值以加快力响应速度、减少力超调量。变阻尼阻抗控制方程为：

(25)

式中，b0为阻抗控制的初始阻尼值，Δb(t)为变阻尼值。力误差产生的阻尼调整值为：

Δb1(t)=Δb1(t-λ)-η(fd-fe)

(26)

式中，λ为系统的采样周期，η为更新率，Δb1为根据力误差生成的阻尼修改值。

(3)估计环境参数，根据估计值在线调整阻抗控制参数。环境的接触力估计值为：

(27)

利用最小二乘算法估计环境的刚度及阻尼，式(27)可修正为：

(28)

(29)

求解式(28)得到环境的估计参数为：

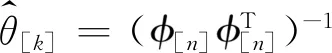
(30)

当机械臂与外界接触时，传感器会连续采集机械臂位置及接触力数据，导致基于最小二乘算法的计算量不断增大，因此将最小二乘算法与递归算法结合，有：

(31)

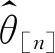
(32)

(33)

(34)

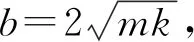
(35)

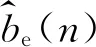
Δb2(t)=Δb2(t-λ)-β(b-bd)

(36)

式中，β为阻尼调参系数，Δb2为根据所估计的环境参数而生成的阻尼修改值。

使用李雅普诺夫方法分析变阻尼阻抗控制系统的稳定性。将式(25)简化为：

(37)

式中，B(t)表示系统不断变化的阻尼值。当进行恒力跟踪时，阻抗控制稳定时的位置修正量为：

(38)

令e为阻抗控制实时的位置修正量，则位置修正量误差E为：

E=e-ed

(39)

为了分析式(37)的稳定性，候选李雅普诺夫函数为：

(40)

式中，V为能量函数，对于任意的误差修正量E，V都不小于0，对V求导，有：

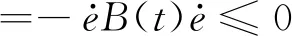
(41)

由式(41)计算结果可知，V的导数小于或等于0，表明李雅普诺夫函数能量一直在减小，而式(40)表明其能量主要与修正量误差E相关，即误差也一直在减小，从而变阻尼阻抗控制系统趋于稳定。

3.2.3 主动接触仿真实验

利用常阻尼及变阻尼阻抗控制在不同外部环境下进行机械臂力控任务仿真模拟实验。为了简化仿真过程，只在Y方向上设置期望力，期望力Fd=diag[0;50;0]，环境刚度分别设置为500、5000、50 000 N/m，环境阻尼统一设置为20 (N·s)/m，在每种环境下的阻抗控制模型阻尼参数分别取50、200、500 (N·s)/m，不同环境刚度条件下的仿真实验结果如图10所示。由图10(a)可见，当环境刚度为500 N/m时，3种常阻尼条件下的接触力均没有超调，但是响应速度都较慢，并且阻尼值越大，相应的响应速度越慢，而采用变阻尼阻抗控制时，相应的力响应速度与阻尼为50 (N·s)/m时的响应速度接近，均能在较低的环境刚度下快速实现力响应；由图10(b)可见，当环境刚度为5000 N/m时，3种常阻尼条件下的接触力响应速度均较环境刚度为500 N/m时的相应值更快，其中阻尼为50 (N·s)/m时的接触力有一定的超调量，而采用变阻尼阻抗控制时，相应的力响应速度与阻尼为200 (N·s)/m时的响应速度接近，没有力超调，响应速度也较快；由图10(c)可见，当环境刚度为50 000 N/m时，3种常阻尼条件下的接触力响应速度均很快，尤其阻尼为50 (N·s)/m时的接触力最大值达到80 N，力超调量达到60%，此外，阻尼为200 (N·s)/m时的接触力也有一定的超调量，而采用变阻尼阻抗控制时，相应的力响应速度与阻尼为500 (N·s)/m时的响应速度接近，其动态力响应在较高的环境刚度下没有出现力超调和不稳定振荡现象。综合上述仿真结果可知，在常阻尼阻抗控制条件下，当环境刚度过低(500 N/m)时，较大的阻尼会降低力响应速度；当环境刚度过高(50 000 N/m)时，较小的阻尼值会引发较大的力超调量，并且产生的振荡力会导致接触不稳定；而采用变阻尼阻抗控制在不同环境中进行力控任务都能实现零稳态误差、低过冲及快速上升的理想力响应。

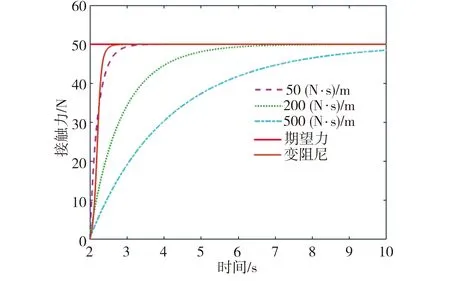
(a)环境刚度500 N/m

4 结语

本文以液压转角自伺服柔顺关节为驱动机构构建机械臂模型，利用仿真模拟实验研究了机械臂与外部环境发生意外碰撞或进行主动接触任务时的主动柔顺控制策略。实验结果表明，当机械臂与外界发生意外碰撞时，采用速度控制策略或基于位置且与PI控制结合的阻抗控制策略，相应生成速度或位置信号，通过将信号传递给关节可驱使机械臂逃离碰撞物，从而有效降低碰撞力；当机械臂在未知的外部环境中执行主动接触任务时，选择一阶力响应模型，根据接触力误差及环境参数估计值来调整阻抗控制阻尼，可使机械臂在与外部环境发生主动接触时实现零稳态误差、低过冲和快速上升的理想力响应。