南海超深水取样钻柱纵向粘滑振动分析

高光海，仇性启，董 辉，许俊良，任 红

(1.中国石油大学(华东) 化学工程学院，山东 青岛 266580；2.中石化胜利石油工程有限公司 钻井工艺研究院，山东 东营 257017)



南海超深水取样钻柱纵向粘滑振动分析

高光海1，仇性启1，董 辉1，许俊良2，任 红2

(1.中国石油大学(华东) 化学工程学院，山东 青岛 266580；2.中石化胜利石油工程有限公司 钻井工艺研究院，山东 东营 257017)

针对南海超深水天然气水合物取样钻柱纵向粘滑振动问题，推导了纵向振动微分方程，采用非线性弹簧单元模拟了钻柱与岩层之间的粘滑摩擦。通过数值求解得到了钻柱纵向振动频率及振动位移，探讨了钻压、钻铤长度及作业水深对钻柱纵向振动的影响。结果表明：钻柱低阶振动频率所对应外载激励周期为1.5～4.0 s，接近南海波浪运动周期，钻柱发生低阶共振几率较大；钻压的增加，使得钻柱振动位移减小；钻铤长度及作业水深的增加使得钻柱振动频率减小、振动位移增加，南海环境下钻柱更易发生低阶共振；钻柱发生1阶共振时振动位移约为近频率振动位移的8倍，共振危害程度较大。

超深水；钻柱；纵向粘滑振动；振动频率；振动位移

我国南海深水海域天然气水合物钻探取样时，取样钻柱顶端与钻井船连接，通过钻井船中动力装置为钻柱提供动力；海水中无隔水管装置，钻柱与海水直接接触；海底岩层中钻柱直接与岩层接触。钻柱长径比较大，钻柱弯曲挠度较大，钻柱结构具有几何与接触双重非线性性质。钻柱在钻井船纵向浮沉运动、钻柱与海底岩层之间纵向摩擦作用、钻柱底部钻头与岩层的相互作用等载荷作用下，其纵向振动特性十分复杂。取样钻柱纵向振动剧烈程度直接关系到钻柱内部取样仪器能否正常定位以及钻探取样过程能否顺利实施。

目前，国内外诸学者对海洋钻井立管及陆地石油钻井中钻柱的纵向振动特性进行了相关研究，取得了丰硕成果。Y Chen[1]等通过变分迭代计算研究了海洋立管固有频率特性；Y Kovalyshen[2]研究了深井钻井中钻柱粘滑振动特性；A Ghasemloonia[3]等研究了钻柱纵向及横向耦合非线性振动特性；Y Hu[4]等采用空间曲梁有限单元模型研究了超深井中钻柱动力学特性；S M Sahebkar[5]等对斜直井中钻柱在随时间变化的轴向载荷作用下的非线性振动特性进行了分析；T G Ritto[6]等采用钻头-岩层非确定性模型分析了钻柱非线性动力学特性；Y A Khulief[7]等对钻柱粘滑自激振动特性进行了研究；R Sampaio[8]等通过建立分线性模型研究了钻柱纵向及扭转耦合振动特性；Y A Khulief[9]等通过拉格朗日与有限单元法相结合分析了钻柱动力学振动特性。国内刘清友、李子丰[10-11]等建立了钻柱纵向振动力学模型及理论计算公式。章扬烈[12]通过大量的理论分析及试验研究，得到了钻柱纵向振动机理及相关减振措施。王文龙[13]等研究了激励位移、钻井液粘度及减震器安装位置等因素对钻柱纵向振动轴向力的影响规律。赵宗彬、肖文生[14-15]等通过ANSYS有限元分析，研究了钻柱纵向振动固有特性并得出了相应的结论。刘进田、闫铁[16-17]等推导了钻柱振动的微分方程及有限元矩阵方程，并进行了实例分析计算。孙千伟[18]等通过解析法以及相关实验研究了管-土轴向动力作用下等效弹簧系数取值问题，确定了不同地质条件下等效弹簧系数取值范围。

鉴于取样钻柱结构及工艺流程的特殊性，基于陆地钻柱及海洋立管纵向振动特性研究现状，建立取样钻柱纵向振动力学分析模型，研究钻柱结构的纵向振动特性。

1 取样钻柱纵向振动微分方程

1.1 基本假设

建立取样钻柱纵向振动力学模型时对一些次要因素进行相应的简化，做如下假设：

1) 钻柱材料均匀且各向同性，在运动和变形过程中始终处于线弹性范围之内。

2) 钻柱横截面为圆环形，忽略钻柱接头的影响。

3) 钻柱内部充满海水，钻柱外部水流为定常流动载荷。

4) 同一纵向位置处，钻柱振动过程所受阻尼以及岩层与钻柱之间摩擦因数皆恒定。

1.2 动力学微分方程

取样钻柱纵向振动模型示意图如图1所示。

图1 钻柱纵向振动模型示意

假设钻柱材料密度为ρ，截面抗拉刚度为E(z)A(z)，阻尼系数为c(z)。假设钻柱横截面在纵向振动过程中始终保持平面，以u(z,t)表示z截面纵向位移，它是截面位置z与时间t的二元函数。取微元段dz，其应变量为：

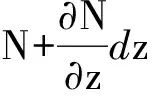
根据牛顿第二定律可得钻柱纵向振动微分方程[10-11]：

(1)

式中：E(z)为位置z处钻柱弹性模量；A(z)为位置z处钻柱横截面积；ρ′为钻井液(海水)密度；g为重力加速度；fm为钻柱微元所受轴向粘滑摩擦力。

1.3 初始条件

1.4 边界条件

1) 海平面处。

海平面处假定钻柱与钻井船连接一起，纵向方向上随钻井船一起做浮沉运动，即：

u(0,t)=U(t)

(2)

其中，u(0,t)为t时刻海平面处钻柱纵向位移；U(t)为钻井船纵向运动位移。

2) 钻头处。

钻井船纵向周期性浮沉运动以及底部岩层的不均匀性使得钻头处所受纵向载荷不断发生变化。根据牛顿第二定律，钻头与岩层互作用纵向动力学模型为：

(3)

其中，mb为钻头质量；uz(t)为t时刻钻头纵向振动位移；fz(t)为t时刻钻头所受到的岩石作用力；p(t)为t时刻作用到钻头上的钻压。

3) 钻柱与海底岩层接触处。

通过静力学迭代计算分析，确定钻柱系统与岩层接触部位。将钻柱与岩层之间的摩擦作用等效为非线性弹簧对钻柱作用，将钻柱节点与非线性弹簧单元节点耦合。通过设置弹簧单元的力学参数，来模拟钻柱与岩层之间的粘滑摩擦作用。

2 数值分析

采用有限单元法将钻柱连续系统离散为n个单元的离散系统，这些单元组成一个有限多自由度系统。

取样钻柱系统振动过程中，始终存在阻尼作用。钻柱纵向振动系统所受阻尼采用工程设计中常用Rayleigh阻尼：

[C]=α[M]+β[K]

(4)

式中：[C]为阻尼矩阵；[M]为质量矩阵；[K]为刚度矩阵；α为钻柱质量阻尼系数；β为钻柱刚度阻尼系数。

α、β取值由钻柱振型阻尼比及振动固有角频率计算得出。

ξ=α/2ωi+βω2/2

(5)

式中：ξ为钻柱振型阻尼比，一般取0.02～0.05；ωi为钻柱第i阶振动固有角频率。

采用ANSYS静、动力学分析模块结合MATLAB、APDL编程模块对取样钻柱纵向振动微分方程进行数值求解。选取以梁单元特性为基础的PIPE59及PIPE16单元分别模拟海水及岩层中钻柱，选取COMBIN39非线性弹簧单元模拟岩层与钻柱粘滑摩擦，选取MASS21单元模拟钻头。

3 纵向振动频率分析

3.1 实例分析

钻柱结构及环境载荷相关参数如表1。

表1 钻柱及环境相关参数

根据表1参数，求得钻柱纵向振动频率如图2所示。

由图2可知，随着阶数增加，钻柱振动频率逐渐增加。钻柱前几阶振动频率较小，外界载荷作用下，钻柱易发生纵向共振。

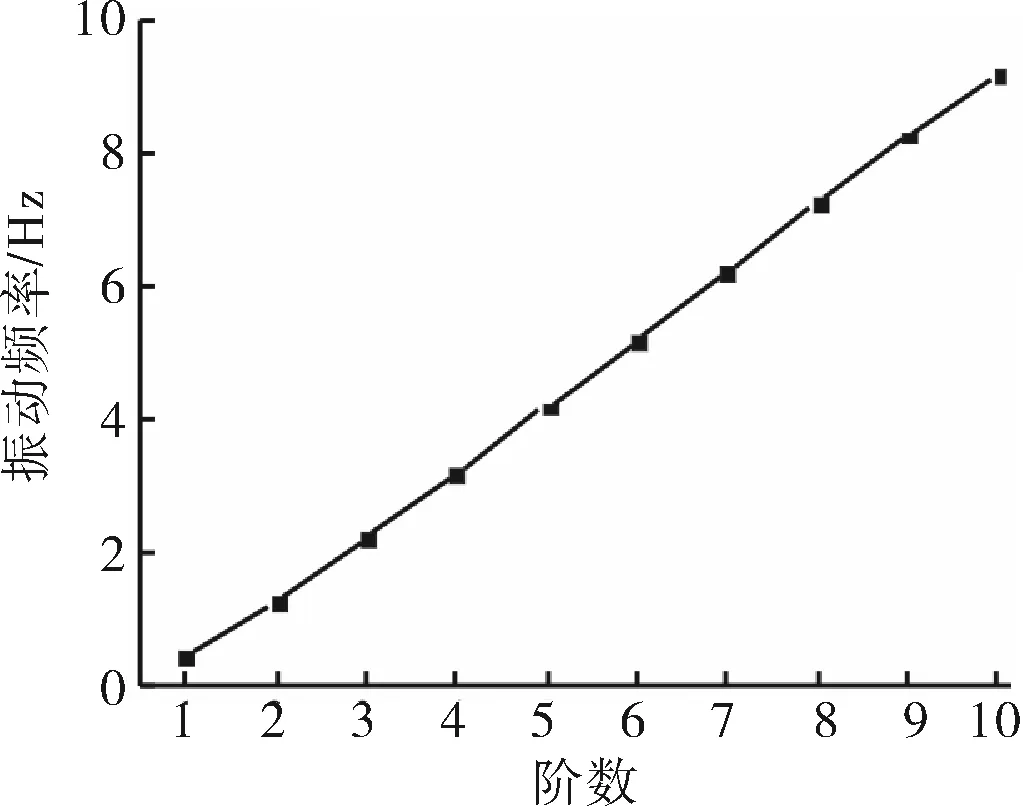
图2 钻柱纵向振动频率

3.2 影响因素分析

1) 钻铤长度。

作业水深2 000 m、岩层深度600 m时，不同钻铤长度下，钻柱纵向振动频率如表2。

由表2可知，随着钻铤长度的增加，钻柱各阶纵向振动频率逐渐减小，即钻铤长度的增加使得钻柱纵向振动周期增加。

2) 作业水深。

岩层深度600 m，不同作业水深时，钻柱纵向振动频率值如图3所示。

表2 钻柱纵向振动频率

图3 不同作业水深时钻柱纵向振动频率

由图3可知，随着作业水深的增加，钻柱纵向振动各阶振动频率不断减小，且随着振动阶数的增加，变化幅度越来越大。作业水深的增加，使得钻柱纵向振动周期增加。

4 纵向振动位移响应分析

取样钻柱钻探取样过程中，钻柱纵向振动位移大小直接关系到钻柱内部取样仪器的正常定位。振动位移过大将使得钻柱内部取样仪器不能正常定位，进而使得取样失败。钻探取样过程中，不同因素对钻柱振动位移影响不同。以下分析不同因素对钻柱纵向振动位移的影响。

4.1 钻压

作业水深2 000 m、岩层深度600 m、钻铤长度取80 m时，不同钻压作用下，钻柱纵向振动最大位移响应曲线如图4所示。

图4 不同钻压下钻柱纵向振动位移曲线

由图4可知，随着钻压的增加，钻柱纵向振动位移逐渐减小，钻柱纵向振动位移最大值所对应频率为钻柱1阶振动频率。相同钻柱结构下，钻压的增加，使得钻柱下部受压区域增大，钻柱纵向振动受到抑制，振动位移减小；钻柱发生1阶共振时，共振位移突然增大，共振位移值约为相近频率正常振动下的8倍。

4.2 钻铤长度

作业水深2 000 m、岩层深度600 m、钻压取200 kN时，不同钻铤长度下，钻柱纵向振动最大位移响应曲线如图5所示。

图5 不同钻铤长度下钻柱纵向振动位移曲线

由图5可知，随着钻铤长度增加，钻柱纵向振动位移逐渐增加，钻柱纵向振动位移最大值所对应频率为钻柱1阶振动频率。相同钻柱长度及钻压条件下，钻铤长度的增加，使得钻柱下部受拉区域增加，钻柱纵向振动增强，振动位移增大；钻柱1阶共振位移值约为相近频率正常振动下的8倍。

4.3 作业水深

岩层深度600 m、钻铤长度250 m、钻压取200 kN时，不同作业水深时，钻柱纵向振动最大位移响应曲线如图6所示。

图6 不同作业水深时钻柱位移曲线

由图6可知，随着作业水深的增加，钻柱纵向振动位移逐渐增加，钻柱纵向振动位移最大值所对应频率为钻柱1阶振动频率。相同钻压条件下，作业水深的增加，使得钻柱下部受拉区域逐渐增加，钻柱纵向振动增强，振动位移增大。

5 结论

1) 推导了取样钻柱纵向振动微分方程。钻柱与岩层纵向粘滑摩擦作用可通过非线性弹簧单元进行模拟。通过数值求解得出了钻柱纵向振动频率及振动响应位移。

2) 南海深水海域取样钻柱1阶振动频率所对应外载荷激励周期在1.5～4.0 s。钻铤长度及作业水深的增加使得钻柱纵向振动频率减小，在南海环境条件下钻柱更易发生1阶共振。

3) 取样钻柱发生1阶共振时振动位移为近频率正常振动位移的8倍。相同条件下，钻压的增加使得钻柱振动位移逐渐减小，钻铤长度及作业水深的增加使得钻柱振动位移逐渐增加。

[1] Chen Y，Zhang J，Zhang H，et al.Re-examination of natural frequencies of marine risers by variational iteration method[J].Ocean Engineering，2015( 94)：132-139.

[2] Kovalyshen Y.Understanding root cause of stick-slip vibrations in deep drilling with drag bits[J].International Journal of Non-Linear Mechanics，2014( 67)：331-341.

[3] Ghasemloonia A，Rideout D G，Butt S D.Analysis of multi-mode nonlinear coupled axial-transverse drillstring vibration in vibration assisted rotary drilling[J].Journal of Petroleum Science and Engineering，2014(116)：36-49.

[4] Hu Y，Di Q，Zhu W，et al.Dynamic characteristics analysis of drillstring in the ultra-deep well with spatial curved beam finite element[J].Journal of Petroleum Science and Engineering，2012(82)：166-173.

[5] Sahebkar S M，Ghazavi M R，Khadem S E，et al.Nonlinear vibration analysis of an axially moving drillstring system with time dependent axial load and axial velocity in inclined well[J].Mechanism and Machine Theory，2011，46(5)：743-760.

[6] Ritto T G，Soize C，Sampaio R.Non-linear dynamics of a drill-string with uncertain model of the bit-rock interaction[J].International Journal of Non-Linear Mechanics，2009，44(8)：865-876.

[7] Khulief Y A，Al-Sulaiman F A，Bashmal S.Vibration analysis of drillstrings with self-excited stick-slip oscillations[J].Journal of sound and vibration，2007，299(3)：540-558.

[8] Sampaio R，Piovan M T，Lozano G V.Coupled axial/torsional vibrations of drill-strings by means of non-linear model[J].Mechanics Research Communications，2007，34(5)：497-502.

[9] Khulief Y A，Al-Naser H.Finite element dynamic analysis of drillstrings[J].Finite elements in analysis and design，2005，41(13)：1270-1288.

[10] 刘清友，马德坤，汤小文.钻柱纵向振动模型的建立及求解方法[J].西南石油大学学报(自然科学版)，1998，20(4)：55-58.

[11] 李子丰，李志刚.钻柱纵向振动分析[J].天然气工业，2004，24(6)：70-73.

[12] 章扬烈.钻柱运动学与动力学[M].北京：石油工业出版社，2001.

[13] 王文龙，胡群爱，刘化伟，等.钻柱纵向振动分析与应用[J].振动与冲击，2011，30(6)：229-233.

[14] 赵宗彬，仇性启，许俊良.深海天然气水合物钻探取心钻柱振动模态分析[J].天然气工业，2011，31(1)：73-76.

[15] 肖文生，王现锋，裴艳丽，等.基于ANSYS的钻柱纵向振动固有频率分析[J].钻采工艺，2011，34(5)：93-95.

[16] 刘进田.下部钻柱振动分析及计算[J].石油矿场机械，2013，42(3)：50-54.

[17] 闫铁，王雪刚，李杉，等.钻柱轴向与横向耦合振动的有限元分析[J].石油矿场机械，2012，41(3)：39-42.

[18] 孙千伟，刘威，李杰.管-土轴向动力相互作用等效弹簧系数取值[J].同济大学学报(自然科学版)，2012，40(8)：1123-1128.

Analysis on Longitudinal Stick-slip Vibration of Ultra-deep Water Drillstring

GAO Guanghai1，QIU Xingqi1，DONG Hui1，XU Junliang2，REN Hong2

(1.CollegeofChemicalEngineering，ChinaUniversityofPetroleum(EastChina)，Qingdao266580，China；2.DrillingTechnologyResearchInstitute，SinopecOilfieldServiceShengliCorporation，Dongying257017，China)

Based on the longitudinal stick-slip vibration of the drillstring in South China Sea，the differential equation of the longitudinal vibration was deduced.The stick-slip friction of the drillstring and rock was simulated through nonlinear spring unit.The vibration frequency and displacement were obtained by using numerical simulation method.The effects of drilling pressure，the length of the drill collar and the depth of water were also discussed in the paper.According to the results，the period of the external load excitation which corresponding to the low-level vibration frequencies of the drillstring is 1.5～4.0 s.The period is close to the period of the wave in south sea of China.The probability of the resonance of the drillstring is large.The vibration displacements decrease owing to the increase of the drilling pressure.The vibration frequencies decrease and the vibration displacements increase owing to the increase of the length of the drill collar and water depth.The resonance displacement is nearly 8 times to the displacement of normal vibration.

ultra-deep water；drill string；longitudinal stick-slip vibration；vibration frequency；vibration displacement

2016-05-18

国家高技术研究发展计划(863计划)课题“天然气水合物钻探取芯工程样机及配套技术”(2013AA092602)；中央高校基本科研业务费专项资金资助项目(16CX06015A)

高光海(1989-)，男，山东禹城人，博士研究生，从事海洋油气管柱力学研究，E-mail：ggh8912@126.com。

1001-3482(2016)11-0008-06

TE952

A

10.3969/j.issn.1001-3482.2016.11.002