浅谈逆矩阵在保密通信中的应用
秦小娜
(江西科技学院,江西 南昌 330098)
浅谈逆矩阵在保密通信中的应用
秦小娜
(江西科技学院,江西 南昌 330098)
摘要:本文在分析线性代数在高职基础教育的基础上,立足学生的基本学情,阐述了逆矩阵在保密通信中的实际应用。
关键词:线性代数;逆矩阵;保密通信
1引言
《线性代数》是讨论矩阵理论、与矩阵相结合的有限维向量空间及其线性变换理论的一门学科。在数学、力学、物理学和技术学科中有各种重要应用,因而它在高等学校基础教学体系中占有重要地位,众所周知,数学是对实际问题的抽象,随着当今科学技术的发展,我们不仅要研究单个变量之间的关系,还要进一步研究多个变量之间的关系,而各种实际问题在大多数情况下可以线性化,而由于计算机的发展,线性化了的问题又可以计算出来,线性代数正是解决这些问题的有力工具。
线性代数这门课本身内容比较抽象,逻辑性又比较强,对高职学生来说容易感觉枯燥,因此要求教师针对不同内容要采取独特的授课方法,充分调动学生积极性和主动性,学生对身边熟悉的事物往往比较敏感,因此,教学过程若能结合生活实际必能激发学生学习兴趣。本文针对逆矩阵在实际生活中的应用进行了探讨。
2基于加密技术的保密通信模型
随着信息时代的发展,保密通信成为了一个重要的研究课题,很多学者为此做了大量的工作,先后提出了许多有效的保密通信模型,其中,基于加密技术的保密通信模型是其中最具活力的一种。
基于加密技术的保密通信模型可简单归纳如下:
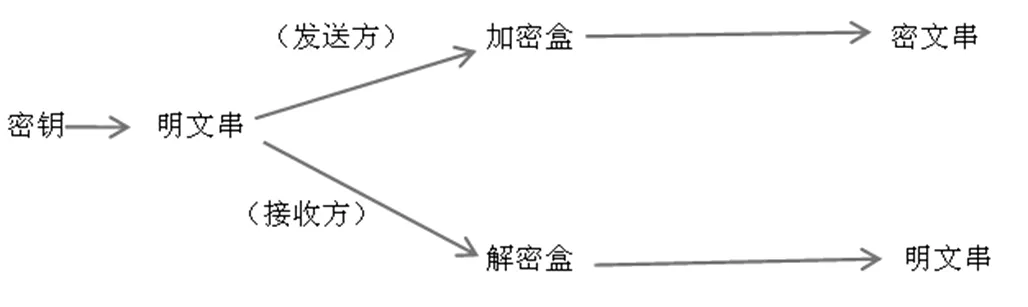
发送方采用某种算法将需要传送的数据加密转换成密文数据发送给接收方,接收方则可以采用相对应的某种算法将密文数据解密转换成明文数据。
显然一种加密技术是否有效,关键在于密文能否被还原成明文。
设有矩阵方程C=AX,其中X为未知矩阵,我们知道,如果矩阵A可逆,则该方程有唯一解,其中A-1是矩阵A的逆矩阵,因此,可逆矩阵可以有效的应用于加密技术。
2.1加密算法
加密时,采用下面的矩阵乘法
B=AX或B=XA,
2.2解密算法
解密时,采用下面的矩阵乘法:
X=A-1B 或X=BA-1
其中,A-1为A的逆矩阵。
2.3加密矩阵的生成
为了便于计算,要求逆矩阵具有整数元素,因此,在选择密文矩阵时,尽可能地使其行列式为1或者-1,我们知道初等矩阵是可逆的,而且初等矩阵的乘积也是可逆的,因此,通信中可以考虑利用若干个初等矩阵的乘积作为编译矩阵,它的生成方法如下:从单位矩阵出发,反复运用第一类和第三类初等变换矩阵去乘他,而其中的k必须取整数,这样得到的矩阵将满足我们的要求。
3应用举例
将26个英文字母依次对应数字1,2,…,26,任选一个行列式为1或者-1的方阵,如
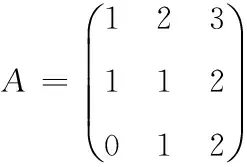
因为
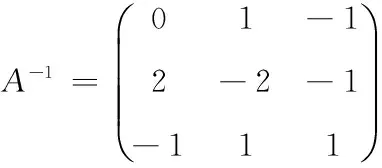
所以断定,所发送信息为you。
参考文献:
[1]侯亚君,林红娟.线性代数[M].北京:机械工业出版社,2012.
[2]陈维新. 线性代数简明教程[M].2版.北京:科学出版社,2008.
[3]李大卫,等.线性代数释疑解难[M].沈阳:东北大学出版社,2001.
中图分类号:TN915
文献标志码:A
文章编号:1671-1602(2016)12-0135-01

