基于数学建模物流网络模型分析

黄 吉 聪

(厦门华天涉外职业技术学院，福建 厦门 361102)



基于数学建模物流网络模型分析

黄 吉 聪

(厦门华天涉外职业技术学院，福建 厦门 361102)

摘要：物流管理分析是目前研究的重点。伴随着计算机技术的发展，大部分物流管理系统通过采用一种新的探索方法——信息数学建模物流管理分析，实现了无人工检索即可获得信息的新技术。目前的文献中基本都是在进行数据仓库方面建立模型，模型的创新点在于引入物流网络模型建立模型算法以处理物流管理系统数据中的噪声数据，进行有效的基于物流管理系统的物流管理分析、实验分析，建立模型的物流管理分析算法模型在存在噪声的物流管理系统数据中起到了建立模型的效果。因而，将该模型应用于数学建模物流管理分析算法，尤其是个性化数学建模是十分合理的。

关键词：模型优化；物流管理分析；数学建模

0引言

物流系统数据发展快速，本文研究物流系统网络模型。不同于物流网络处理的数据为一维的向量，卷积物流网络的输入是二维的图像，中间层也是由二维平面构成，每个平面由物流元组成，物流元之间互相独立，没有连接。卷积物流网络主要由卷积层、池化层、全连接层、损失层等组成。卷积层中，前一层的二维平面与一个参数可学习的核进行卷积产生一个数值，并输入到激活函数中，激活值作为卷积层的物流元值。

模型通过单隐藏物流网络模型进行基于数学建模物流管理分析。物流网络模型分为单层和多层两种。

1物流管理数学建模

物流网络模型是单层网络的一种，“物流优化模型”这一术语已经逐渐开始变得包罗万象。物流优化模型至少已经成为一种针对当前数据的便捷处理手段，科学家们用它来指代自学习和源自新数据(大部分属于物流网络数据)的模式发现等大量前沿技术。而人们对于物流优化模型定义的探寻似乎也延伸到了更为广泛且界线加权的领域内。

物流网络数据发展快速，目前，多数企业已建成一体化企业级数据中心平台，能够满足日常业务的需求，但物流网络数据时代对传统数据中心的数据存储能力、数据处理能力、数据交换能力、数据展现能力以及数据挖掘能力都提出了更高的要求，物流网络数据对传统数据中心提出了新的挑战[1]。

物流网络数据的重要性越来越大，通过不同的方法得到数据进而进行分析已经成为主流[1]。

物流网络数据时代，对数据的处理速度和时效性提出了更高要求，而当今社会日益加剧的商业竞争让每个企业都希望能通过实时分析报表和结果数据来随时掌握企业运营状况，并迅速做出决策和判断。以电力电量平衡测算为例，需要实时采集电网数据、实时分析、实时计算，快速测算结果，并反馈至电力调度部门进行有序用电执行预案的实时决策，如果相关数据获取不及时则会大大影响调度部门对有序用电的分析和决策[2]。

物流网络数据的非结构化改变了数据分析模式。传统数据分析以结构化数据分析为主，业务分析更是以被动式信息接受为主。物流网络数据时代下，随着数据的累积和增加，可做的分析和对比也越来越多。通过对大量的非结构化进行分析，从而揭示非结构化之间隐藏的关系、模式和趋势；通过结构化数据、半结构化数据、物流网络数据的融合关联分析，研究文本分析、数据挖掘、图形分析、空间分析等数据分析模式，为决策者提供不同角度不同形式的分析判断依据。

物流网络模型的特点是对于单隐层前馈物流网络模型，在学习精度比较高的前提下比一般的算法更加快速。(x1,x2,…,xn)是输入数据,即表达数据，(w1,w2,…,wn)是权值，存在f为选取的激活函数。激活函数的作用是对输入数据进行预处理，目的是将不规整的数据进行归一化处理，激活函数为：

通过运算求出最终值。

分类的模型为：

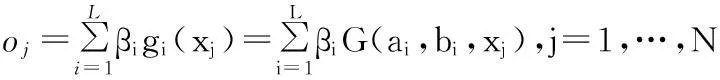
上式中,βi为输出权值向量,ai为输入权值向量,oj为与Yj相对应的实际输出向量,bi为偏置。

单隐层物流网络模型学习的输出误差最小值。

最小化损失函数，根据最小二乘原理。H+为H的广义逆矩阵。通过训练物流网络模型建立数据模型。

物流网络模型在物流网络数据中的运行速度非常快，在同样分类精度的条件下，相比BPNN、SVM、决策树等有着时间复杂度的优势。因此，与常用的数学建模分类算法比较后，物流网络模型的优点明显。

2改进数学建模方法

在存在异常值的物流网络数据中，对比物流网络模型，改进物流网络模型的分类性能。

要处理物流异常数据首先要对物流数据进行筛选。对物流数据进行字段筛选探究手段大致可以分为两种：基于物流数据过滤的对物流数据进行字段筛选探究手段、基于物流数据的缠绕属性筛选方法的对物流数据进行字段筛选探究手段。

特征的筛选尤为重要。基于物流数据过滤的对物流数据进行字段筛选探究手段是一种计算效率较高的探究手段，它采用某种特定的判别标准对数据的属性进行打分，并筛选分值较高的属性。目前用的较多的判别准则有概率长度探究手段都是采用属性对样本的预测贡献大小的一个度量探究手段。物流数据过滤探究手段使用合适的准则来快速评价属性的好坏，适用于对样本物流数据进行初步字段筛选。物流数据过滤探究手段的优点是可以很快地排除很大数量的非关键性的异常值属性，缩小优化属性字段搜索范围，用来作为属性的预选器非常好，对物流数据进行字段筛选过程非常快；并且属性物流数据属性筛选的过程是与具体的预测的数据挖掘方法独立的，与预测算法无关。它的显著缺点是不能保证筛选出一个规模较小的最优属性字段。

基于物流数据的缠绕属性筛选方法的对物流数据进行字段筛选探究手段是一种有监督的对物流数据进行字段筛选探究手段。在属性的筛选过程中，要使用一个预测器算法对筛选的属性进行评价，一般情况下评价准则是筛选该属性之后的数据能否在预测器的预测中获得较高的预测精度，即在对物流数据进行字段筛选的过程中，使用包含被筛选属性的数据集来训练预测器，根据训练得到的预测器在测试集上的实验结果来评价所选属性的优劣。

物流大数据的非结构化改变了数据分析模式，传统数据分析以结构化数据分析为主，业务分析更是以被动式信息接受为主。大数据时代下，随着数据的累积和增加，可做的分析和对比也越来越多。通过对大量的非结构化进行分析，从而揭示非结构化之间隐藏的关系、模式和趋势。

基于物流数据的缠绕属性筛选方法的对物流数据进行字段筛选探究手段能够考虑属性之间的相关性，保证获得规模较小的属性字段，通过此种手段筛选的属性能够保证数据集的较高预测精确度；但是它的缺点是该探究手段的数据挖掘方法时间复杂度高，且筛选出来的属性对预测算法有一定的依赖性。

加权物流网络模型经过在误差和进行加权。加权物流网络模型二次规划的方法是将隶属度加权到经验物流管理上，单加权物流网络模型的方法同样也是将权值加权到最小二乘的位置，每一行的输入值xj都在误差ej,m上乘以wj,m(m=1,2,…,M)。

本文提出双加权物流网络模型二次规划，将样本物流网络数据复制两份，即数据量由N变成2*N，分别以不同的概率属于不同的类别。

最小化：L的前面是模型复杂度，后面是加权后的经验物流管理，u为权值。e为误差。换成拉格朗日乘子。得出拉格朗日乘子。(w,b,e,η,αj,rj)表示拉格朗日系数和误差值。通过求(w,b,e,η,αj,rj)偏微分，进而可以得出最终的结果。

预测问题在科研领域已经广泛应用，数据挖掘与机器学习广泛应用于数据中。本文优化建模算法策略来对非结构化的物流数据进行运输预测。当非结构化的物流数据存在异常值的情况下，提出了加权建模和双加权建模算法处理异常值。传统预测算法在领域上(非结构化的物流数据运输预测)存在可优化部分。数据分析存在异常值的非结构化的物流数据进行仿真数据分析。

利用数学建模对非结构化的物流数据进行运输预测，综述了相关理论，首先介绍微阵列数据，进而非结构化的物流数据中对重要属性进行字段筛选的规则，说明了对重要属性进行字段筛选的重要性，以及传统分类器。并简介了建模的算法，论述了建模的历史、建模的算法流程、建模的算法优势等。对建模进行了综述，进而提出加权的建模算法，与双加权建模算法。加权算法与双加权算法为别人提出，本文的创新点在于将加权算法与双加权算法嵌入到数学建模中，进而将此算法应用在非结构化基因数据中。通过实验分析，对非结构化的物流数据集的预测仿真，与传统的建模预测比较，本文数据分析的算法在非结构化的物流数据存在异常值时，分组精度要高于建模预测算法。证明优化的算法成功应用于非结构化的物流数据存在异常值。

3数据分析

数学建模分析，总运费很有可能不一样。设xij，i=1，2；j=1，2，3，4，表示从仓库Ai运往零售点Bj的产品数量，从A1,A2两仓库运往四地的产品数量总和应该分别是a1单位和a2单位，所以xij应满足

x11+x12+x13+x14=a1

x21+x22+x23+x24=a2

本文通过网络模型进行优化分析。应用模糊方法进行优化。求解方式通过网络方法得出结论。

均值池化层中损失函数对输入的梯度为当前层的梯度除以池化单位区域的面积，表示如下：

卷积物流网络中的激活函数有多种形式：

物流到B1,B2,B3,B4四地的产品数量应该分别满足他们的需求量，即xij还应满足以下条件：

x11+x21=b1

x12+x22=b2

x13+x23=b3

x14+x24=b4

最后xij表示运量，不能取负值，即xij∈0(i=1，2；j=1，2，3，4)，我们希望在满足供需要求的条件下，求xij，i=1，2；j=1，2，3，4，使总运量最省。总的物流费用为

minz=c11x11+c12x12+c13x13+c14x14+c21x21+c22x22

+c23x23+c24x24

通过物流网络模型的方法能够取得最优的方法以建立费用模型。

模型对总的物流费用进行了物流网络模型的分析，得出最优线路是第二第三的组合。

参考文献：

[1]陈希.关于开设“数学建模初步”课程的思考[J].福建商业高等专科学校学报，2014，(1).

[2]刘德海,夏少刚.“数学建模”分析方法的局限性及对教学方法的启示[J].高等理科教育，2014，(3).

[3]左元斌.管理类专业数学建模课程教学改革探讨[J].盐城工学院学报：社会科学版，2014，(4).

[4]石岿然.管理类数学建模精品课程教学方法之探讨[J].管理观察，2014，(18).

[5]张智广.浅谈数学建模课程的教学[J].职业时空，2014，(2).

[6]杜玉琴.数学建模在经济管理中的应用[J].现代商业，2013，(18).

[7]冯期.浅谈数学建模在物流领域中的应用论文[J].中国校外教育，2014，(4).

[8]吴育华,何雁群.数学建模在工业工程中的应用[J].工业工程，2014，(4).

[9]李妍峰,陈泞,杨琴.工业工程专业《数学建模》课程教学改革思路[J].管理科学文摘，2014，(4).

[10]刘永新.物流数学建模教学改革与实践[J].天津职业院校联合学报，2014，(2).

责任编辑：柴造坡

doi:10.3969/j.issn.1674-6341.2016.03.015

收稿日期：2016-01-15

作者简介：黄吉聪(1979—)，男，福建漳浦人，在读物流工程硕士，讲师，统计师，经济师。研究方向：数学建模、物流工程、模糊数学、统计分析。

中图分类号：O29

文献标志码：A

文章编号：1674-6341(2016)03-0033-03