问渠哪得清如许,为有源头活水来
——一道数列问题的探究与反思
◎高福岚
(河北衡水一中,河北 衡水 053000)
问渠哪得清如许,为有源头活水来
——一道数列问题的探究与反思
◎高福岚
(河北衡水一中,河北 衡水 053000)
在数学的学习中掌握方法,可以不变应万变,归纳重要题型的解题方法尤为重要.
例 已知数列{an}中,a1=5,a2=2,an=2an-1+3an-2,n≥3,n∈N*,求数列{an}通项公式.
解法一 由题意得,an+an-1=3an-1+3an-2=3(an-1+an-2),
即:{an+an-1}是一个公比为3的等比数列,
an+1+an=(a2+a1)×3n-1=7×3n-1,


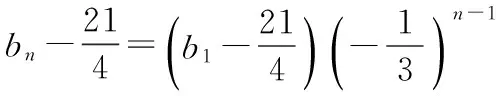


解法一首先把相邻三项的关系的递推公式转化为相邻两项的关系的递推公式,构造新等比数列,在新等比数列通项公式(两项的递推公式)基础上再转换为熟悉的两项的递推公式.最后构造等比数列求解.
解法二 由题意得,an+an-1=3an-1+3an-2=3(an-1+an-2),
即:{an+an-1}是一个公比为3的等比数列,
an+1+an=(a2+a1)×3n-1=7×3n-1,
an+an-1=7×3n-2,
于是有an+1-an-1=14×3n-2,
已知a1=5,所以有
(a3-a1)+(a5-a3)+…+(a2k-1-a2k-3)
=a2k-1-a1=14×32-2+14×34-2+…+14×32k-4

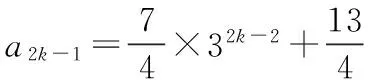
同理已知a2=2,所以有
(a4-a2)+(a6-a4)+…+(a2k-a2k-2)
=a2k-a2=14×33-2+14×35-2+…+14×32k-3
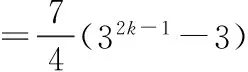
水击中流扬帆进,乘风破浪正当时。今天,云南民营经济已成为云南省拉动投资增长的主要动力、创业就业的主力军、财政收入的重要来源、促进对外贸易的主要力量、繁荣市场的主体力量。东风已至,在改革开放的伟大历史进程中,云南民营经济将继续演绎“春天的故事”。

解法二也是首先把相邻三项的关系的递推公式转化为相邻两项的关系的递推公式,构造新等比数列,在新等比数列通项公式(两项的递推公式)基础上构造奇(偶)数项的递推公式(熟悉的两项的递推公式),最后累加求解.
解法三:
由题意得,an+an-1=3an-1+3an-2=3(an-1+an-2),
即:{an+an-1}是一个公比为3的等比数列,
an+1+an=(a2+a1)×3n-1=7×3n-1,

当n为奇数时,


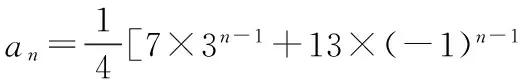
解法三也是首先把相邻三项的关系的递推公式转化为相邻两项的关系的递推公式,构造新等比数列,在新等比数列通项公式(两项的递推公式)基础上求得前n项和.进而数列求解.

反思 人们常说“饮水思源”,我们做题又何尝不是呢?笔者不禁想到南宋诗人朱熹《观书有感》的一句诗“问渠哪得清如许,为有源头活水来”.只要我们抓住问题的相似处和本质,多联系,多想象,就能做到砸实基础,举一反三,触类旁通,提升思维能力与创新能力.

