高等数学数形结合教学法的探索
赵琳

摘 要:数形结合是高等数学教学中非常重要的一种教学方法,其让学生的学习在抽象的理论学习过程中逐渐形成具象的学习思维,让学生能够将数量关系和空间图形进行有效结合,从一定程度上简化了学习的难度。该文从数形结合教学法的重要性入手,提出相应的教学策略,希望可以为相关人士对数学结合教学法的研究提供借鉴和参考。
关键词:数形结合 思想方法 以数表形 以形验数
中图分类号:O175.5 文献标识码:A 文章编号:1674-098X(2016)05(a)-0169-02
高等数学是一门非常重要的基础理论课程,其学习的效果不仅对学生的本学科学習产生非常重要的影响,而且对学生其他学科的学习质量也产生极大作用。高等数学具有非常严谨的逻辑性,抽象理论学习是其非常重要的内容。也正是因为此,很多学生在进行高等数学学习的时候,出现了极大的不适应,造成其理解上的困难。
1 高等数学数形结合教学法的重要性
通过对高等数学的研究,可以发现,高等数学学习中的几何问题是探究微积分的重要起源,其在高等数学中的每一个章节中都会有所涉及。将高等数学中的几何现象运用抽象的数学分析语言进行描述,就形成了高等数学中的概念定理。很多学生直接学习概念定理具有一定的难度,但是反其道而行,将其运用几何图形的方式进行展现,直观形象的理解抽象概念,寻找相应的证明思路就显得非常简单。
数形结合的过程便是将抽象的理论与图形结合在一起,将数学中的抽象概念进行形象化描述,通过具象展示的方式让学生的抽象思维和形象思维共用,让学生对高等数学的理论概念进行简化理解的一种学习方法。数形结合将“数”的理念和“形”的特点结合在一起,两者彼此促进,相互配合,为学生的高等数学学习提供一个新的思路。学生通过数形结合的教学方式进行高数学习,不仅不会感觉到数学的乏味,反而会探究到高数的趣味,能够有效提升学生的学习积极性,有效提升学生的学习质量。用此方法进行教学,能让学生的学习思想获得启发,是激发学生思考和兴趣的重要途径。
2 高等数形结合教学方法在教学中的应用
2.1 运用数形结合进行数学思维的阐述
数形结合教学方法在教学中更好的应用需要教师对教学思维的重视,注重在解题的过程中注重对数学思维的阐述,通过习题应用的方式让数形结合的思想得到最好的表达。比如,例题如下:
曲线具有凹凸性,其是曲线的几何表现形式,但是如何使用代数的形式对其进行定义和表达呢?
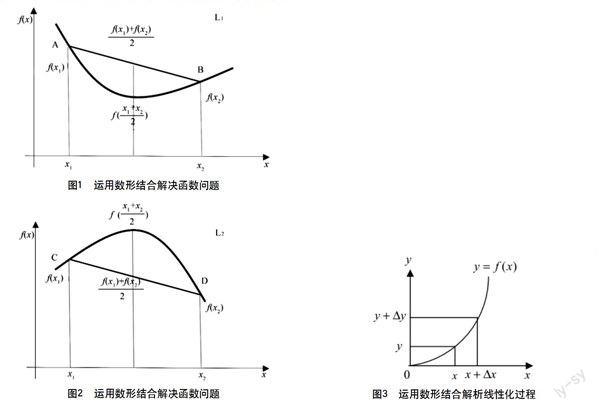
对于这个案例,教师在进行教学的时候,便可以让学生通过对图形的观察来深化学生的数形结合思想。(如图1、图2)
通过观察,可以发现,图1、图2中曲线弧L1和L2上,弦AB、CD与相应弧的位置关系,以及在点
2.2 运用数形结合解析线性化过程
线性化学习同样是高等数学教学中非常重要的教学内容。因为其所具有的抽象性,很多学生对其学习都感觉到非常困难。但是运用数形结合的方式对线性化过程进行解析则可以让其更加简单化,其学习的效果也非常好。
函数的该变量与自变量的变量关系是y=Ax的形式,通过数形结合的方式能够让学生更加清楚地了解线性化过程,并对此问题进行相应的解答。
2.3 通过数形结合的方式启发学生思考
数学学习最佳的方式莫过于让学生进行自主思考,让学生的学习主动性得到充分发挥。运用数形结合的方式能够有效启发学生的探索思维,帮助学生养成勤于思考的好习惯,让学生的学习更加具有主动性。比如
作为重要的极限概念,其应用范围非常广泛,实用定义和极限运算法则对其进行证明则非常困难,这时候就需要运用到夹逼准则进行证明。此时学生便可以通过数形结合的方式对其进行证明。
3 结语
数形结合的教学方法与数形结合的思想相得益彰,其在提升学生学习能力的基础上能够发挥非常大的作用和影响,在培养学生学习思维、创新能力等方面产生的作用更加不容低估。教师要对此教学方法进行深入研究和探索,通过让学生在具体习题中进行应用的方式深化学生对此教学方法的认识,让数形结合的教学方法深入学生生活、思维的各个方面。
参考文献
[1]王爽,李秀珍,赵永谦,等.高等数学数形结合教学法的研究与实践——以山东建筑大学为例[J].山东建筑大学学报,2015(6):600-606.
[2]龚冬保,褚维盘,叶正麟.数形结合方法实例分析——陕西省大学生高等数学竞赛赛题系列分析之一[J].高等数学研究,2013(2):28-31.

