等价无穷小代换在求和式极限中的应用
仝淑芳, 郑 军(.西南交通大学交通运输系,四川峨眉山640; .西南交通大学基础课部,四川峨眉山640)
等价无穷小代换在求和式极限中的应用
仝淑芳1, 郑 军2
(1.西南交通大学交通运输系,四川峨眉山614202; 2.西南交通大学基础课部,四川峨眉山614202)
[摘 要]等价无穷小代换经常用于求函数乘积的极限,讨论了如何利用等价无穷小代换求函数和式的极限.
[关键词]等价无穷小;极限;定积分;广义积分
1 引 言

利用定积分定义与等价无穷小量代换是求极限的两种常用方法,由于等价无穷小量一般不能在加、减法中直接代换以求极限,所以上述两种方法难以直接综合应用.在文献[1]中,作者证明了,在求和因子f(x)有不低于一次的增长性条件下,即当时,可以采用类似于等价无穷小代换的技巧,从而使利用定积分定义与等价无穷小量代换可综合使用.本文的主要结论是,在求和因子没有增长性条件的假设下,证明一类求和式的极限可以采用等价无穷小代换的技巧,使得求和式极限时不仅可以综合利用定积分与等价无穷小代换,也可以利用无界函数的广义积分定义与等价无穷小代换.在下文中,将数列
时,在求和式极限

2 主要结果
若存在,则


即


故


由数列极限定义得

由此可得

注1 在文献[1]中,f(x)与h(x)有不低于一次的增长性,本文减弱了该条件,使得f(x)与h(x)可以有其它的增长方式,例如f(x)与h(x)形式上可以为等.
推论1 ①设函数f(x),h(x)满足:
(ii)在0的某一去心邻域内h(x)≠0且不改变符号;
其中g(x)是定义在(a,b]上的函数,g(x)≠0,且存在常数M及p∈[0,1),使得

则

②设函数f(x),h(x)满足:
(ii)在0的某一去心邻域内h(x)≠0且不改变符号;
其中g(x)是定义在[a,b)上的函数,g(x)≠0,且存在常数M及p∈[0,1),使得

则



即时,
令

则有

由定理可得

注2 ①在文献[1]中,g(x)为闭区间[0,1]上的有界函数,在本文的推论中,g(x)可以减弱为开区间上的无界函数.
②若g(x)为闭区间[0,1]上的有界函数,则推论中g(x)的条件自然满足.
推论2 ①若函数f(x),g(x)满足:
(i)g(x)在上可积(0,1],且存在常数M及p∈[0,1),使得

(ii)f(x)在x=0处可微,且f(0)=0(或f(0)=1),则

②若函数f(x),g(x)满足:(i)g(x)在[0,1)上可积,且存在常数M及p∈[0,1),使得
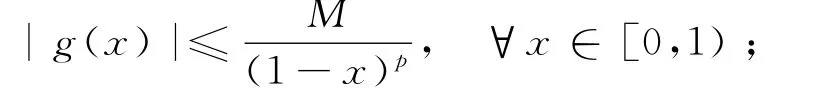
(ii)f(x)在x=0处可微,且f(0)=0(或f(0)=1),则

证 只需注意到无界函数的反常积分的定义(见[2])及g(x)的增长性,利用推论1及文献[1,3]的方法即可证明.
注3 若g(x)在[0,1)上连续,且存在常数M及p∈[0,1),使得对,有

则由无界函数的反常积分的比较审敛法(见p266,定理6,[2]),g(x)在[0,1)上可积.同理,若g(x)在(0,1]上连续,且存在常数M及p∈[0,1),使得对,有,则g(x)在[0, 1)上可积.
下面给出本文结论的几个应用,其中例1和例3取自文献[3].
解 令f(x)=sinx,h(x)=x,则



例2 求
解 注意到
令


则


例3 求

选取




例4 求
解 注意到
令


显然f(x)在x=0处可微,且f(0)=1.由于
且


由推论2可得

[参 考 文 献]
[1] 华梦霞,陈庆.利用等价无穷小代换求和极限[J].大学数学,2013,29(1):134-137.
[2] 同济大学数学系.高等数学[M].北京:高等教育出版社,2014.
[3] Yuan N.A Discussion on a limit theorem and its application[J].College Mathematics,2006,22(1):90-94.
An Application of the Equivalent Infinitesimal in Solving Sum Limitations
TONG Shu-fang1, ZHENG Jun2
(1.Department of Traffic and Transportation,Southwest Jiaotong University,Emeishan 614202,China;2.Department of Basic Course,Southwest Jiaotong University,Emeishan 614202,China)
Abstract:The equivalent infinitesimal is often used in solving limitations with multiplicativity factors.In this paper,it is discussed how to apply the equivalent infinitesimal to solve limitations with additive factors.
Key words:equivalent infinitesimal;limitation;integration;generalized integration
[基金项目]中央高校基本科研业务费(10801X10096022)
[收稿日期]2015-06-20
[中图分类号]O172.2
[文献标识码]C
[文章编号]1672-1454(2016)01-0105-05

