关于贝特朗奇论的新观点——基于点的均匀分布假设进行建模分析

王奕可（中央财经大学保险学院，北京102206）



关于贝特朗奇论的新观点——基于点的均匀分布假设进行建模分析

王奕可
（中央财经大学保险学院，北京102206）

［摘 要］针对贝特朗问题进行建模，给出在适当的附加均匀分布假设下，概率解可以取到区间［0，1］内任一值的结论．为得出在无附加条件下贝特朗问题的解，同样采用建模方法，通过改变模型参数使附加条件变为贝特朗问题的内含条件，进而导出结果，以此判明既有的诸主流解法的正确性．

［关键词］贝特朗奇论；均匀分布；几何概型

1　引 言

1899年，法国数学家约瑟夫·贝特朗（Joseph Bertrand，1822－1900）在其著作《概率计算》中提出了贝特朗问题，即：在圆内任作一弦，求其长度超过该圆内接正三角形边长的概率．对于该问题有着诸多看似合理却大相径庭的解答，显然违背了几何概率的性质，于是产生了著名的“贝特朗奇论”．

数年来，围绕贝特朗问题，形成了如下几种主流的解法［1］：

（i）由于对称性，考虑某指定方向的弦．作一直径垂直于该方向，只有交直径于与之间的弦满足要求，所求概率为

（ii）由于对称性，固定弦的一端点，令另一端点在圆周上作随机移动．在固定端点作一切线，则与此切线交角在60°与120°之间的弦满足要求，所求概率为

（iii）圆内弦的位置被其中点唯一确定，在圆内作一同心圆，其半径仅为大圆半径的一半，则大圆内弦的中点落在小圆内时才满足要求，所求概率为

针对上述三种解法，诸多学者各持对唯一解的不同看法，张敏、何小亚［2］已在其论文中作出归纳，此处不再赘述．另外值得注意的是，石启亮［3］采用随机模拟的方法得到贝特朗问题的正确答案为，郑长波、孟宪涛［4］给出了答案能够取到区间，即有无穷多解的结论．

本文的目标则是建立模型来说明在适当的附加均匀分布假设下答案能够取到区间［0，1］内的任一值，借此说明附加的均匀分布假设对问题解答的影响，从而基于样本空间选取时的均匀分布假设构造新的模型来导出贝特朗问题的正确解．为此，先将贝特朗问题转化为如下等价命题：

2　弦组选取

由于圆内的弦有无穷多条，通常的做法是基于对称性来选取具有代表性的一组弦，在本文中采用更为严谨的说法，基于均匀分布（或等可能性）假设来选取弦组．

如图，作与单位圆同心、半径为k（≥1）的圆，则单位圆中任意弦的延长线必然与大圆有交．假设点在大圆上均匀分布．以大圆上的点向单位圆作割线，必然能够得到单位圆内所有的弦．现规定劣弧沿圆周的顺时针方向为该劣弧的正方向，如图，在劣弧XY上X相对Y为正，以Y为端点沿YX方向作射线，交大圆于唯一点P．

上述方式表明了存在单位圆内除直径外的所有弦到大圆上的点的映射．将所有且仅映射到大圆上某一定点的弦纳入弦组，则得到弦组到大圆上的点的双射．由于各弦组同质且互不相交，现选取大圆上一点P，显然以点P对应的弦组具有代表性．特别的，由于每个弦组内含有无穷多条弦，故是否考虑至多一条落在单一弦组内的直径不会影响最后结果的正确性．下述各模型都将采用以此种方式选取的弦组进行讨论．

中国经济和社会发展步入新时代，在人口老龄化、高龄化、空巢化等大背景下，在抚育子女和赡养老人的压力下，在照顾家庭和努力工作的夹缝中，面对人们对更美好家政服务的需求，我们需要更深刻地认识家政服务供给侧的提质和升级问题，用高质量培训推动家政服务进入新时代。

3　［0，1］区间模型

回顾第一种解法，将同一方向的一组弦映射为在一条直径上的点来计算概率，实质上是在贝特朗问题题设之外附加了点在直径上均匀分布的假设．依照同一思路，该模型假设点在直径所在的直线上均匀分布．

在弦组选择中，已设点P所在的大圆半径为k（≥1）．如图所示，取大圆上一点M且OM与OP夹角不超过，点P对应的弦组中的弦XY（或其延长线）交OM与点A．显然，在点P固定的条件下，弦XY能够被点A所唯一确定，因此选择点A作为样本点来考虑概率．为确定样本空间，过点P引单位圆的切线PQ交OM于点N′，显然点A只能落在线段ON′内．在单位圆内作半径为的同心圆，过点P引该同心圆的切线PT交OM于点N，联系第三种主流解法可以得出，当且仅当点A落在线段ON内时，弦XY将穿过半径为的同心圆，长度大于

现在由几何概率的定义，可以得出贝特朗问题的概率表达式

设∠MOP＝θ，由切线PT，PQ可以得出以下四个三角函数式

于是

即贝特朗问题的概率解在该模型中被描述为关于大圆半径k和点均匀分布的直径与OP连线夹角θ的函数P （k，θ）．由于P （k，θ）在连续，而

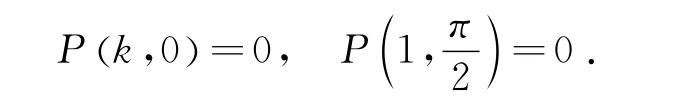
由连续函数的介值性，P （k，θ）的函数值可以在区间［0，1］内任意取值，这也就证明了在适当的附加均匀分布假设下，贝特朗问题的概率解可以取到区间［0，1］内任一值的结论．

不难发现，虽然一题多解应与概率的性质相违背，但是在不同的均匀分布假设下，各答案都有其正确性，因此出现多解的原因是在题意之外由解题者附加的均匀分布假设．下面就将通过模型将附加的均匀分布假设内化为贝特朗问题的内含条件，推导唯一的正确解．

4　同心圆模型

既设点P所在大圆半径为k（≥1）．在将弦映射为大圆上的点时，为避免牵涉其余可能隐含的均匀分布假设，所作的映射要求尽可能简单．一个符合要求的映射如下：因为弦组中所有的弦所在直线都通过点P，现作弦XY的反向延长线，交大圆于异于P的另一点Z，如图所示．过点P引关于单位圆以及单位圆内半径为的同心圆的切线PQ，PT分别交大圆于点Q′，T′，延长PO交大圆于O′．显然点P对应弦组中的弦只能映射到上，且上任一点与且仅与弦组内的一条弦对应．当点Z落在内时，弦XY长度大于，由几何概率的定义可知：

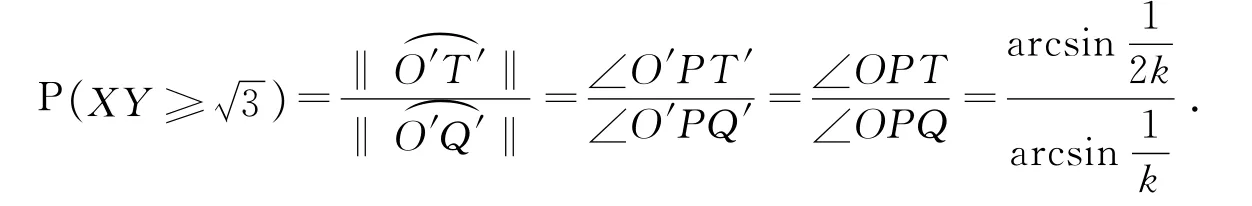
需要再次强调的是，固定k的取值时，均匀分布假设仅为“点在半径为k的圆周上分布均匀”，这是非常弱的均匀分布假设，因为大圆圆周和单位圆圆周以外的平面区域的点的密度可以是任意的．为了“去掉”这一假设，取k＝1，即大圆与单位圆重合，均匀分布假设则退化为“点在单位圆上均匀分布”，这与由圆周上随机两点确定弦的等可能性相符，也是贝特朗问题的内含条件．此时得到

即为贝特朗问题的正确解．

另外，当k＝1时，得到的是第二种传统解法仅在以OP为界的半圆里讨论的情形．由以上讨论可知，第二种传统解法的答案和过程都是正确的．

5　关于映射构造的一些思考

在模型中，将弦映射为一系列均匀分布的点尤为重要．例如第三种传统解法中，虽然将所有的弦都映射到自身中点，但弦的中点在圆内并不是均匀分布的，这一结论已由黄晶晶在其论文《关于贝特朗悖论的新思考》［5］中证明，因此本文选择先构造均匀分布假设，再将弦映射到假设均匀分布的点上．但是这样一来，要如何构造合理的映射，便成为问题．

在同心圆模型中，存在另一种合理的映射构造方式：过圆心引弦的垂线并延长与大圆相交，如图，弦XY的中垂线交大圆于点Z，而过圆心O引两切线PT，PQ以及OP的垂线得到样本空间的边界点O′，Q′和弦长大于的临界点T′．

由垂直关系同样能够得到概率解的表达式

但是，如果采取以点P为圆心作弧将弦（中点）映射到大圆的方法，却不能够得到正确的结果．对比三种映射，可以认为同心圆模型中的“延长线映射”和此处的“圆心垂线映射”是保持比例关系的映射，而“圆弧映射”是改变了比例关系的映射．再进一步思考，贝特朗问题的内在要求包含“点在单位圆圆周上均匀分布”，与“大圆上的点均匀分布”一同构成类似于极坐标网络的均匀放射（如图），因此过圆心引垂线能够保持比例关系不变，大圆上的点相当于圆心的射影；而“延长线映射”则可以看成是点P向大圆上其余点射影，弦则是射影的路径在单位圆内的部分，参考射影几何学的有关内容，射影不会改变比例关系，因此“延长线映射”不会改变比例关系，所以能够保持正确的概率解．相较之下，同心圆模型中的“延长线映射”更优，因为它避开了贝特朗奇论之争中的一个特殊点——圆心［6］，使得答案正确性得到了更进一步的保障．

6　结 论

本文在传统解法的基础之上，采用构造的模型的方法，证明了在适当的附加均匀分布假设（或等可能性条件）的情况下，贝特朗问题的概率解可以取到区间［0，1］内任一值，而后同样采用建模方法分析去掉附加的均匀分布假设（或等可能性条件），回归贝特朗问题的本身内含条件，从而导出贝特朗问题唯一的正确解，证明了引言中第二种传统解法的正确性．

［参 考 文 献］

［1］ 茆诗松，程依明，濮晓龙．概率论与数理统计教程［M］．北京：高等教育出版社，2011：28－29．

［2］ 张敏，何小亚．贝特朗悖论之争的终结［J］．数学教育学报，2015，24（3）：51－54．

［3］ 石启亮．解读贝特朗（Bertrand）悖论［J］．数学教学，2005，（10）：32－34．

［4］ 郑长波、孟宪涛．关于圆上随机弦奇论的解析［J］．沈阳师范大学学报，2012，30（2）：164－167．

［5］ 黄晶晶，黄世同．关于贝特朗悖论的新思考［J］．昆明师范高等专科学校学报，2004，26（4）：10－12．

［6］ 苏同安．都是圆心惹的祸——“贝特朗悖论”新说［J］．中学数学高中版，2010，（1）：64．

The New Viewpoint of Bertrand Paradox——Modeling and Analyzing Based on the Assumption of a Uniform Distribution for Points

WANG Yi－ke
（Central University of Finance and Economics，School of Insurance，Beijing 102206，China）

Abstract：For the Bertrand’s question，this paper will model to show the conclusion that the probability can be equal to any value in the interval［0，1］in condition of an appropriate additional assumption of a uniform distribution for points．In order to the answer of the Bertrand’s question without any additional assumptions，the method of modeling will be also adopted．The additional assumption of the model can be converted into the inherent requirement of the Bertrand’s question by changing the parameter of the model，then the answer will be derived．Therefore，the correctness of many traditional viewpoints is also shown．

Key words：Bertrand Paradox；uniform distribution；geometric probability

［收稿日期］2015－09－25

［中图分类号］O211．2

［文献标识码］B

［文章编号］1672－1454（2016）01－0044－05