MCKD结合RSGWPT的轴承早期故障诊断方法

陈祥龙， 张兵志， 江鹏程， 冯辅周

(1. 装甲兵工程学院机械工程系， 北京 100072； 2. 北京特种车辆研究所， 北京 100072)

MCKD结合RSGWPT的轴承早期故障诊断方法

陈祥龙1， 张兵志2， 江鹏程1， 冯辅周1

(1. 装甲兵工程学院机械工程系， 北京 100072； 2. 北京特种车辆研究所， 北京 100072)

为解决受背景噪声和信号传递路径等因素影响，轴承早期故障特征微弱，难以有效诊断出轴承故障的问题，提出了一种最大相关峭度解卷积(Maximum Correlated Kurtosis Deconvolution, MCKD)结合冗余第二代小波包变换(Redundant Second Generation Wavelet Package Transform, RSGWPT)诊断轴承早期故障的方法。结果表明：该方法基于MCKD增强原始信号中存在的周期性冲击成分，以最大相关峭度为指标筛选RSGWPT小波包节点，能够凸显故障特征敏感频带，提取故障特征；通过分析车用变速器轴承内、外圈的早期故障数据发现，该方法能够清晰地诊断出轴承早期故障信息，验证了其有效性。

最大相关峭度解卷积；冗余第二代小波包；滚动轴承；故障诊断

当滚动轴承的内、外圈和滚动体等发生故障时，轴承会以一定的通过频率产生宽带冲击，并激励轴承系统产生冲击衰减响应，在振动信号中表现出频率调制和非平稳等特点[1]。然而，受背景噪声和信号传递路径等因素影响，微弱的调制源信号极易被其他成分淹没，难以诊断轴承早期故障。

Sawalhi等[2]最早提出最小熵解卷积(Minimum Entropy Deconvolution, MED)，并将其应用于地震波的分析处理中。MED是一种盲解卷积信号处理方法，能够增强信号中的瞬态冲击成分，广泛应用于机械故障诊断领域。Endo等[3]将MED与AR模型相结合，并将其应用于齿轮箱断齿等故障特征冲击成分的检测；王宏超等[4]将MED与稀疏分解相结合，增强了稀疏分解的抗干扰能力；隋文涛[5]结合MED和经验模式分解，提取出轴承故障特征；然而，唐贵基等[6]和McDonald等[7]发现MED在检测周期性瞬态冲击时效果并不理想，但针对此问题，McDonald等[7]考虑信号中瞬态冲击成分的周期性设计了相关峭度，构造出最大相关峭度解卷积(Maximum Correlated Kurtosis Deconvolution, MCKD)，用于增强信号中周期性瞬态冲击成分，但MCKD是一种全频域的信号处理方法，在检测故障特征敏感频带时并不理想。

第二代小波变换在非稳态分析方面的优势适用于机械故障诊断领域。段晨东等[8-9]依据预测方差最小原则构造非线性小波，提取瞬态冲击故障特征；张超等[10]结合第二代小波变换与集合经验模式分解，分离复合故障的耦合特征，并提取出故障特征频率。针对第二代小波变换的频率混叠问题，周瑞等[11-12]提出一种冗余第二代小波包变换(Redundant Second Generation Wavelet Package Transform, RSGWPT)，具有时不变特性，能够精确匹配信号中的瞬态故障特征，抑制频率混叠，凸显真实的故障特征敏感频带。

基于此，笔者提出利用MCKD增强信号周期性故障特征，并借助相关峭度筛选RSGWPT小波包节点，以期凸显故障特征敏感频带及诊断轴承早期故障。

1 理论依据

1.1 MCKD基本原理

线性时不变系统的振动信号模型可表示为

x=hd*d+he*e，

(1)

式中：x为测量信号；d为周期性冲击序列；e为环境噪声；hd和he分别为系统和环境的滤波器系数。

MCKD增强信号周期性特征的过程为：对测量到的机械振动信号x迭代地选取长度为L的有限冲击响应滤波器f，使滤波后的零均值信号y具有最大的相关峭度以及最小的环境噪声，以增强信号中的周期性冲击成分，逼近原始故障周期性冲击序列d，其具体表达式为

(2)

当移位数为1时，长度为N的零均值信号y关于解卷积周期参数T的相关峭度CK定义为

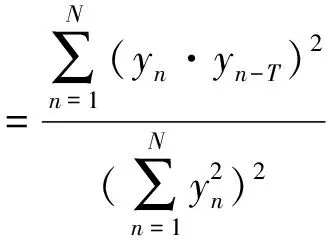
(3)

当移位数为M时，相关峭度定义为

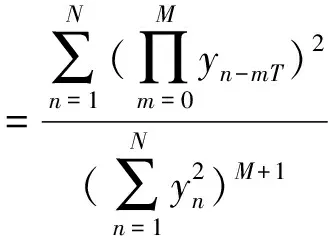
(4)

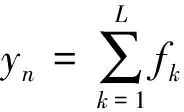
Mcdonald等[7]证实了峭度仅能指示单独的冲击成分，相关峭度能指示周期性冲击成分，因此相关峭度在周期性故障检测中的效果更理想。MCKD通过选取使信号相关峭度最大的有限冲击响应滤波器f增强故障特征。以M=1为例，有

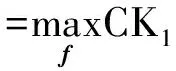
(5)

(6)

式中：

r=0,T,2T,…,mT；

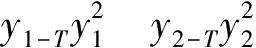
1.2 RSGWPT基本原理

第二代小波变换分裂与合成过程中的上、下采样操作，导致了变换结果中存在频率混叠；小波包变换能将小波变换未细分的高频部分作进一步的分解，因而具有更好的时频分析能力[13]。基于冗余提升方案的RSGWPT能够抑制频率混叠，具备时不变特性，能够更好地匹配故障的时频特征；通过均匀地划分信号频带，能够凸显故障特征敏感频带，有效提取微弱故障特征。其构造如下[11-12]：

1)在2l尺度上的RSGWPT分解表示为

(7)

式中：Sl,i为2l尺度上第i(i=1,2,…,2l)个小波节点系数；Pl+1和Ul+1分别为2l尺度上的冗余预测器和冗余更新器。

2) 在2l尺度上的RSGWPT重构表示为

(8)

3) 2l尺度上的Pl和Ul的表达式分别为

(9)

(10)

2 MCKD结合RSGWPT的故障诊断方法

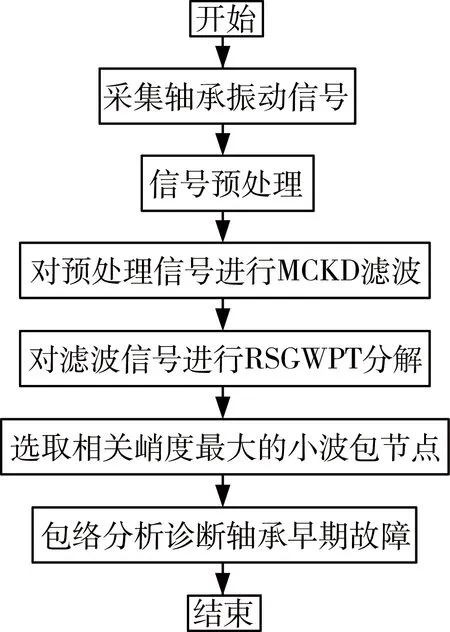
图1 MCKD结合RSGWPT的轴承早期故障诊断流程

针对因轴承早期故障特征微弱而难以有效诊断出轴承故障的问题，笔者提出结合MCKD和RSGWPT的新方法用于诊断轴承早期故障。该方法的诊断流程如图1所示。MCKD作为一种新兴的盲解卷积信号处理方法，通过考虑信号中故障冲击的周期性，具有抑制背景噪声干扰的作用、增强信号故障特征的能力；但由于MCKD是一种全频域信号处理方法，无法直接凸显轴承故障特征敏感频带，因此其在轴承早期故障诊断中的应用受到制约。RSGWPT继承第二代小波变换，不依赖傅里叶变换，能够精确匹配信号的瞬态冲击特征，具有计算速度快和抗频率混叠等特点；RSGWPT变换结果的时不变特性使其获得精确的非稳态信号时频分析能力。因此，笔者将MCKD与RSGWPT相结合，并利用相关峭度在指示信号周期性冲击特征中的优越性，以其为指标筛选最佳RSGWPT小波包节点，增强微弱故障特征的同时凸显出故障特征敏感频带，解调故障特征，并诊断轴承早期故障信息。

3 仿真分析

滚动轴承内圈故障数学模型[2,15-16]构造为

(11)

式中：x(t)为轴承仿真信号；n(t)为噪声信号；A(t)为调制信号；h(t)为故障冲击信号；τi为第i次故障冲击相对于平均故障周期T的微小随机波动，τ～N(0,0.05/fr)，其中fr为轴承转频；fn为系统固有频率;C为阻尼系数。

设置轴承内圈故障通过频率fi=1/T=100Hz，fr=20 Hz，fn=4 000 Hz，采样频率fs=12 000 Hz，阻尼系数C=2 000，信噪比SNR=-15dB，其仿真信号及包络谱如图2所示。由图2(b)可以看出：在强背景噪声下，仿真信号中的瞬态冲击成分完全被噪声淹没。由图2(c)可以看出：信号包络谱中无法有效识别出故障特征频率。

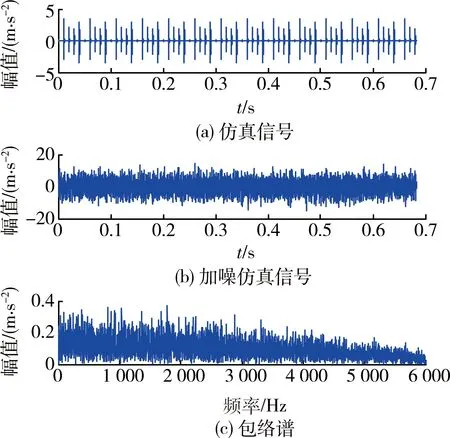
图2 仿真信号及其包络谱

仿真信号经MCKD滤波增强信号故障冲击特征后，对滤波信号进行3层RSGWPT分解，得到8个小波包节点。首先，各小波包分解节点的相关峭度值如图3(a)所示，可以看出第6个小波包节点具有最大的相关峭度值；其次，解调第6个小波包节点的包络信号如图3(b)所示，可以看出包络信号并不具有明显的冲击特征；最后，包络信号的频谱结果如图3(c)所示，可以看出第6个小波包节点的包络谱中内圈故障特征频率fi及其倍频2fi、3fi、4fi的幅值清晰、明显且突出，并在频域中占据主导成分，说明此方法能够清晰提取仿真信号的故障特征。因此，仿真分析认为，MCKD与RSGWTP结合能够有效降低背景噪声干扰，提取微弱故障特征，诊断轴承早期故障。

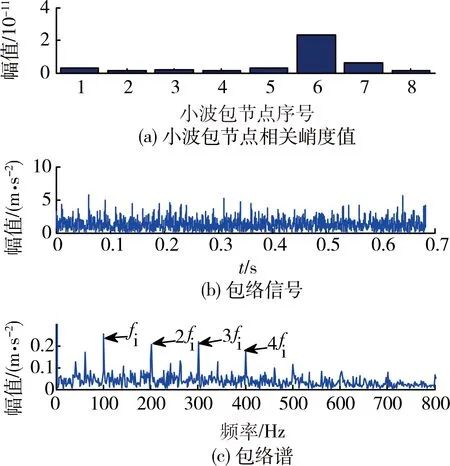
图3 MCKD结合RSGWPT的仿真分析结果

4 试验分析

从BJ2020S车用变速器试验台采集输出轴支撑轴承的振动信号，输出轴支撑轴承型号为6307N深沟球轴承，振动传感器安装在对应输出轴支撑轴承径向的机体光滑处。采用电火花加工法分别在2只堪用轴承的内圈设置尺寸微小的点状缺陷，模拟轴承内圈点蚀剥落故障。

采集振动信号时变速器置于2挡，传动比为2.33，输入轴电动机转速为1 090 r/min，输出轴转速约为468 r/min，对应输出轴转频为7.8 Hz，内圈通过频率为34.08 Hz。试验装置结构如图4所示。

图4 BJ2020S变速器试验装置示意图

图5 一组轴承内圈故障信号的时域波形及其包络谱

图5为一组轴承内圈故障信号的时域波形及其包络谱，可以看出：很难直接提取有价值的故障特征信息。

为了验证笔者所提出方法的有效性，首先对内圈故障信号先进行MCKD滤波以增强故障冲击特征，再对滤波信号进行3层RSGWPT分解。图6为MCKD结合RSGPT的试验分析结果，可见：第7个小波包节点信号具有最大的相关峭度值；第7个小波包节点的时域波形存在较清晰的周期性冲击成分；包络谱中存在清晰的内圈故障特征频率fi及其倍频，且故障特征频率在频域中占据主导成分，证明笔者提出的方法能够有效诊断出轴承故障。

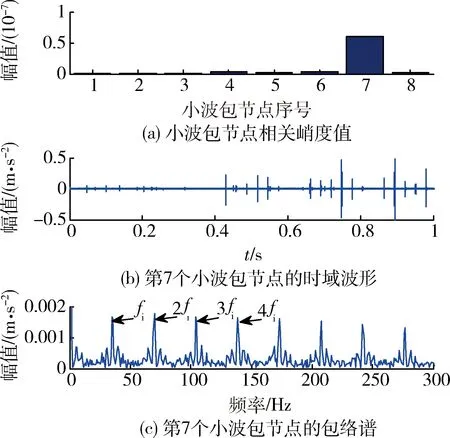
图6 MCKD结合RSGWPT的试验分析结果

为了进一步验证笔者提出方法的必要性，对上述内圈故障信号的MCKD滤波信号直接进行包络谱分析，如图7(a)所示；同时，对上述内圈故障信号仅进行3层RSGWPT分解后，筛选最大相关峭度的节点进行包络分析，结果如图7(b)所示；为方便对比，图6(c)显示在图7(c)中。由图7可以看出：3种方法均能有效提取出内圈故障特征频率及其倍频，但笔者提出的MCKD结合RSGWPT的方法具有更显著的分析结果，能够改善滚动轴承微弱故障提取效果。

图7 包络谱对比

5 结论

针对因轴承早期故障特征微弱而难以有效诊断出轴承故障的问题，笔者提出了MCKD和RSGWPT相结合诊断轴承早期故障的新方法。试验分析结果表明：

1) MCKD作为全频域信号处理方法，能够降低噪声等因素对故障信号的干扰，增强信号中的周期性冲击成分；

2) RSGWPT时不变特性和时频分析能力使其具有良好的微弱故障特征提取能力；

3) MCKD与RSGWPT相结合，既能增强信号故障冲击成分，有利于提取微弱故障特征，又能凸显故障特征敏感频带，诊断出轴承的早期故障。

[1] 肖云魁. 汽车故障诊断学 [M]. 2版. 北京: 北京理工大学出版社, 2006: 254-256.

[2] Sawalhi N, Randall R B, Endo H. The Enhancement of Fault Detection and Diagnosis in Rolling Element Bearings Using Minimum Entropy Deconvolution Combined with Spectral Kurtosis[J]. Mechanical Systems and Signal Processing， 2007, 21(6): 2616-2633.

[3] Endo H, Randall R B. Enhancement of Autoregressive Model Based Gear Tooth Fault Detection Technique by the Use of Minimum Entropy Deconvolution Filter[J]. Mechanical Systems and Signal Processing， 2007, 21(2): 906-919.

[4] 王宏超， 陈进， 董广明. 基于最小熵解卷积与稀疏分解的滚动轴承微弱故障特征提取[J]. 机械工程学报， 2013, 49(1): 88-94.

[5] 隋文涛. 基于EMD和MKD的滚动轴承故障诊断方法[J]. 振动与冲击， 2015, 34(9): 55-64.

[6] 唐贵基， 王晓龙. 基于包络谱稀疏度和最大相关峭度解卷积的滚动轴承早期故障诊断方法[J]. 中国机械工程， 2015(11): 1450-1456.

[7] Mcdonald G L, Zhao Q, Zuo M J. Maximum Correlated Kurtosis Deconvolution and Application on Gear Tooth Chip Fault Detection[J]. Mechanical Systems and Signal Processing， 2012, 33: 237-255.

[8] 段晨东， 何正嘉， 姜洪开. 非线性小波变换在故障特征提取中的应用[J]. 振动工程学报， 2005(1): 134-137.

[9] 段晨东， 何正嘉. 一种基于提升小波变换的故障特征提取方法及其应用[J]. 振动与冲击， 2007(2): 10-13.

[10] 张超， 陈建军， 郭迅. 基于第2代小波和EMMD的转子系统复合故障诊断[J]. 振动、测试与诊断， 2011(1): 98-103.

[11] 周瑞. 基于第二代小波的机械故障信号处理方法研究[D]. 哈尔滨：哈尔滨工业大学, 2009.

[12] 鲍文， 周瑞， 李宁， 等. 采用非降采样第二代小波变换的信号降噪方法[J]. 中国电机工程学报， 2008(20): 82-87.

[13] Randall R B， Antoni J， Chobsaard S. The Relationship between Spectral Correlation and Envelope Anlysis in the Diagnostics of Bearing Faults and other Cyclostationary Machine Signals[J]. Mechanical Systems and Signal Processing, 2001, 15(5): 945-962.

(责任编辑:尚菲菲)

Early Fault Diagnosis of Bearing by Combining MCKD and RSGWPT

CHEN Xiang-long1, ZHANG Bing-zhi2, JIANG Peng-cheng1, FENG Fu-zhou1

(1. Department of Mechanical Engineering, Academy of Armored Force Engineering, Beijing 100072, China； 2. Beijing Special Vehicle Research Institute, Beijing 100072, China)

Because the influences of background noise and signal transfer attenuation, it is difficult to diagnose the bearing fault with weak features at early fault stage. In order to solve this problem, a new method is proposed by combining Maximum Correlated Kurtosis Deconvolution (MCKD) with Redundant Second Generation Wavelet Package Transform (RSGWPT) to diagnose early bearing faults. Simulation analysis demonstrates that the proposed method, which can enhance periodical fault impulses included in raw signals and select RSGWPT nodes by maximum correlated kurtosis factor, can detect fault-sensitive frequency bands and diagnose bearing faults. Analyses of bearing early inner and outer race fault data that come from an automobile transmission demonstrate that the proposed method can clearly extract bearing fault features. Then the validity of the proposed method is verified.

Maximum Correlated Kurtosis Deconvolution (MCKD); Redundant Second Generation Wavelet Package Transform (RSGWPT); rolling bearing; fault diagnosis

1672-1497(2016)05-0040-05

2016-07-07

军队科研计划项目

陈祥龙(1989-)，男，博士研究生。

TH133.3;TP206+.3

A

10.3969/j.issn.1672-1497.2016.05.008