多射击模式下防御效率分析与计算
李龙跃, 刘付显, 赵慧珍
(空军工程大学防空反导学院, 陕西 西安 710051)
多射击模式下防御效率分析与计算
李龙跃, 刘付显, 赵慧珍
(空军工程大学防空反导学院, 陕西 西安 710051)
针对红方(防御方)防御蓝方(进攻方)目标的射击战斗过程,研究了多射击模式下红方射弹分配和防御效率计算方法。首先,在“射击—射击”策略下,基于给定的射弹数和目标数,给出了红方获得最大防御效率时射弹分配方法;其次,在“齐射—观察—齐射”策略下,考虑射击次数和齐射弹数等因素,给出了红方多次射击防御效率迭代递推生成方法;最后,通过实例分析对射弹分配和防御效率计算方法进行了验证,并对内含规律进行了讨论。
射击模式;齐射—观察—齐射;防御效率;生成函数
很多军事作战问题可以抽象为红方(防御方)防御蓝方(进攻方)的射击战斗问题,如:地空导弹射击空气动力目标或弹道目标的防空战斗过程,或高炮对空射击、陆军坦克交战和水面舰艇编队防空等类似的防御性对抗过程[1-2]。防御效率可以理解为红方对达成防御战斗目标程度的度量,与单发杀伤概率、可射击次数和蓝红方攻防实力等因素密切相关。射击模式直接影响防御效率,本文设定射击模式包括2层内容:一是单次射击拦截弹数量,如对目标进行单发射击或多发齐射;二是射击策略,如选择采用“射击—射击”策略或“射击—观察—射击”策略。由于不同射击模式对红方防御效率有较大影响,因此研究射击策略、射弹数量、杀伤概率、射击次数、目标类型等与防御效率之间的内在影响规律至关重要。文献[3-9]作者等对相关问题进行了研究,但这些研究将“射击—射击”策略或“射击—观察—射击”策略分开,且以单因素研究为主,对“齐射—观察—齐射”策略的研究不充分。针对以往研究的局限性,笔者在多种射击模式下研究红方射弹分配和防御效率计算方法,旨在为一类蓝红射击对抗问题在射击模式选择和防御效率计算上提供借鉴。
1 “射击—射击”策略
在“射击—射击”策略下,假设红方共有N枚射弹,若蓝方目标之间无差别,令红方单发杀伤概率为p,则防御效率(EffectivenessofDefense,ED)E=1-(1-p)N。若蓝方目标共有k种类型,红方对第i种类型蓝方目标的单发杀伤概率为pi(i=1,2,…,k),则ED可记为
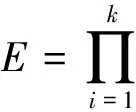
(1)
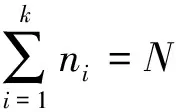
(2)
式(2)两边求微分后,得到

以射击3类蓝方目标(k=3)为例,可得到以下方程:
-ln(1-p1)(1-p1)n1[1-(1-p1)n1]-1E=λ。
(3)
-ln(1-p2)(1-p2)n2[1-(1-p2)n2]-1E=λ,
(4)
-ln(1-p3)(1-p3)n3[1-(1-p3)n3]-1E=λ。
(5)
式(3)除以(4)得到

(6)
解式(6)可得

推广可得[10]
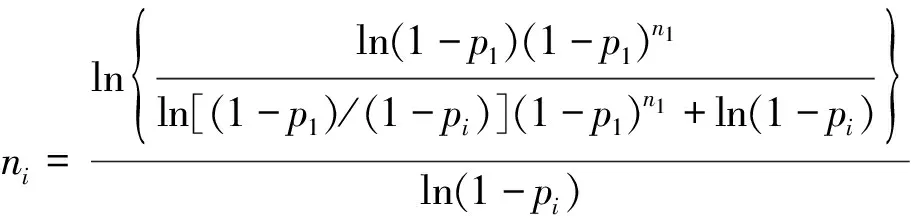
(7)
其中i=2,3,…,k-1。由式(7)可以看出:在已知杀伤概率的情况下,只需要确定n1便可以计算得出ni。
式(5)可以写成
-ln(1-p3)(1-p3)N-n1-n2[1-(1-p3)N-n1-n2]-1E=λ,
(8)
式(3)除以式(8)可得
F(n1)=ln(1-p1)(1-p1)n1[1-(1-p3)N-n1-n2]-
ln(1-p3)(1-p3)N-n1-n2[1-(1-p1)n1]=0,
(9)
式(9)中n2可以通过式(7)求得,因此式(9)中的未知量只有n1,由此可以解出n1。将式(9)进行推广得到
F(n1)=ln(1-p1)(1-p1)n1[1-(1-pk)N-n1-n2-…-nk-1]-
ln(1-pk)(1-pk)N-n1-n2-…-nk-1[1-(1-p1)n1]=0,
当0
(10)
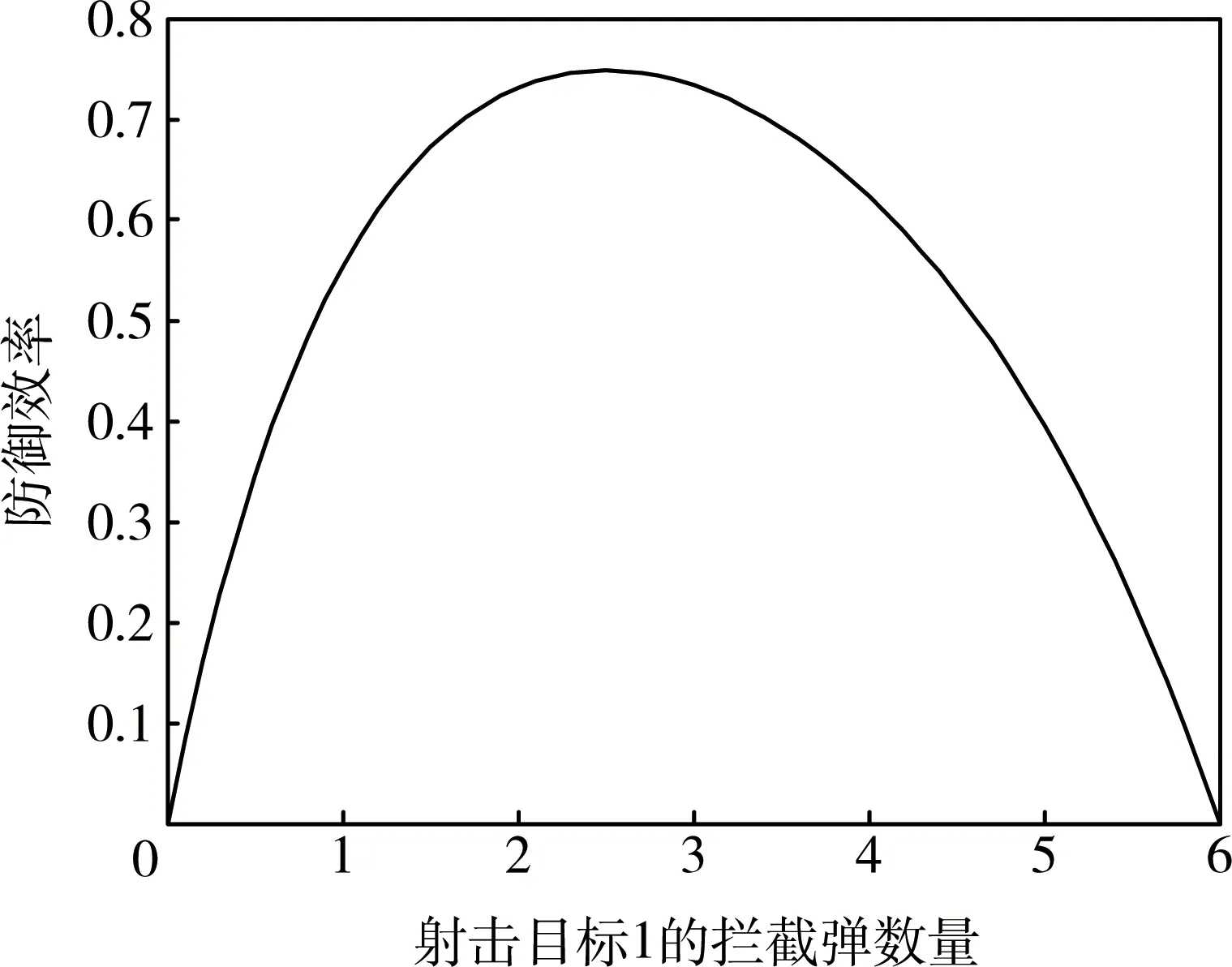
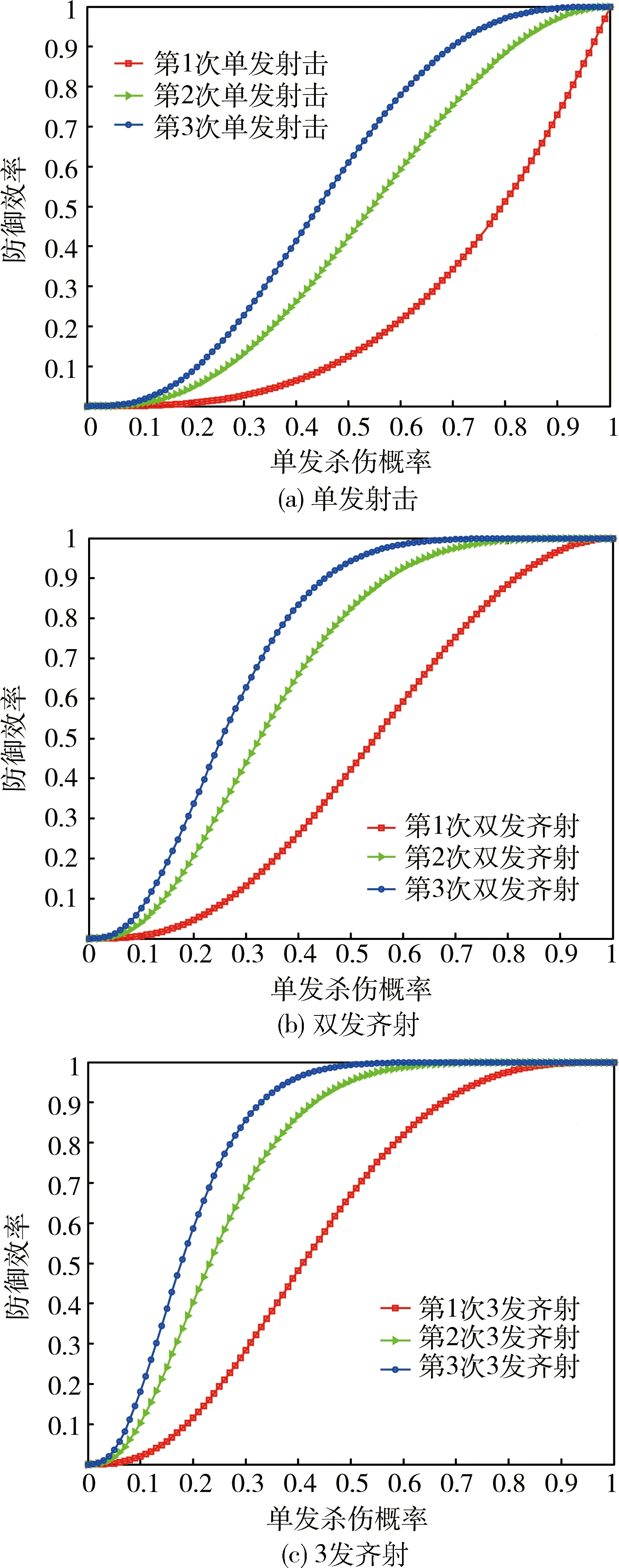
由式(10)可见:0 将对t个目标进行i次射击后,i个目标突防成功的概率表示为 (11) (12) 为求得“齐射—观察—齐射”策略下的最大ED,根据递推关系建立动态规划模型: (13) 式中:i=0,1,…,n,边界条件为 E(n,t=0,s)=1, (14) (15) 由式(14)、(15)可见:若蓝方目标数量为0,则红方ED为100%;若蓝方目标数量不为0,但射击次数为0,则红方ED为0。式(12)中的γ为变量,为方便研究,假定“齐射—观察—齐射”策略下的γ是定值,即红方每次对目标齐射的射弹数γsalvo是一定的,则有nsalvoγsalvo=N,其中γsalvo≥0,nsalvo为可齐射的次数。定义剩余s次射击机会、射击t个目标的杀伤成功概率分布P(0≤x≤t)可由递推生成函数 Gs(nsalvo,t)= (16) 表示,式中:1次齐射的失败概率qsalvo=(1-p)γsalvo,成功概率psalvo=1-(1-p)γsalvo; 剩余射击次数的递归算子定义为 如果用P(x=j)表示杀伤j个目标的概率,则有 射击机会只有1次(s=1)时,根据式(16)有 G1(nsalvo,t)=(qsalvo+psalvo)min(nsalvo,t); (17) 射击机会有2次(s=2)且nsalvo>t时,第2次齐射的生成函数为 b(t,qsalvo)(α1); (18) (19) 式中:α1、α2分别为第1、2次射击后突防成功的目标数量。由此可以推广射击机会有s次且nsalvo>t时,第s次齐射的生成函数为 psalvo)βs-1b(βs-2,qsalvo)(αs-1), (20) 式中:β0=t (21) 式中:cij为相应的多项式系数。 红方共有6枚射弹,蓝方来袭目标共有2个,红方对2个目标的杀伤概率分别为0.6和0.4。在“射击—射击”策略下,图1为ED随射击目标1的拦截弹数量的变化曲线,可以看出:在n1=2.55时ED最大,且仅有一个最大值,取整后结果为向2个目标分别射击3枚弹。图2为F(n1)随射击目标1的拦截弹数量的变化曲线,可以看出:F(n1)为单调递增函数,在n1=2.55时F(n1)=0。可见:图1、2求得的n1结果一致,验证了采用第1节方法求解n1的鲁棒性。 图1 ED随射击目标1的拦截弹数量的变化曲线 图2 F(n1)随射击目标1的拦截弹数量的变化曲线 在“齐射—观察—齐射”策略下,当目标无差别时,假设蓝方目标有3个,红方最多有6次齐射机会,即nsalvo=6,红方剩余可射击次数s=3。图3为在“齐射—观察—齐射”策略下,红方单发杀伤概率、齐射次数、齐射弹数和防御效率之间的关系仿真结果。 图3 “齐射—观察—齐射”策略下仿真结果 从图1-3可以看出:在红方有多次射击机会的前提下,“射击—观察—射击”策略优于“射击—射击”策略;在“射击—观察—射击”策略下,选择多次、多发齐射能有效提高防御效率。原因在于:如果给定红方射弹数和蓝方目标数,选择“射击—射击”策略时,红方防御效率是凹函数[10],具有一个极大值,可直接根据二分法求出射弹的分配方案;选择“齐射—观察—齐射”策略时,红方的防御效率随着射击次数和齐射弹数的增加而单调递增。 在多种射击模式下,笔者基于数学归纳法给出了“射击—射击”策略下红方射弹分配方法和“齐射—观察—齐射”策略下红方防御效率的迭代递推计算方法,结果表明:上述方法能辅助理解类似问题中射击策略、射弹数量、杀伤概率、射击次数等与防御效率之间的关系,且计算简单、结果可靠,具有工程应用推广价值。然而,红方齐射弹数和射击次数不能无限增加,下一步将结合成本、资源等因素研究红方射击模式优化问题。 [1] 李龙跃, 刘付显, 赵麟锋. 对多波次目标直接分配到弹的反导火力规划方法[J].系统工程与电子技术, 2014, 36(11): 2206-2211. [2] 李龙跃, 刘付显, 梅颖颖. 末段反TBM火力-目标匹配优化及APSO求解算法[J].系统工程与电子技术, 2013, 35(5): 993-999. [3] Soland R M. Optimal Terminal Defence Tactics when Several Sequential Engagements are Possible [J]. Operations Research, 1987, 35(4): 537-542. [4] Huma N, Asif M. An Optimal Dynamic Threat Evaluation and Weapon Scheduling Technique [J]. Knowledge-based Systems, 2010, 23: 337-342. [5] Glazebrook K, Washburn A. Shoot-Look-Shoot: A Review and Extension [J]. Operations Research, 2004, 52(3): 454-463. [6] 李龙跃, 刘付显, 田振浩, 等. 双层反导协同模式分析与距离度量优选法[J]. 装甲兵工程学院学报, 2016, 30(4): 57-61. [7] Aviv Y, Kress M. Evaluation the Effectiveness of Shoot-Look-Shoot Tactics in the Presence of Incomplete Damage Information [J]. Military Operations Research, 1997, 3(1): 78-89. [8] Armstrong M J. Effective Attacks in the Salvo Combat Model: Salvo Sizes and Quantities of Targets [J]. Naval Research Logistics, 2007, 54(1): 66-77. [9] Armstrong M J. The Salvo Combat Model with Area Fire [J]. Naval Research Logistics, 2013, 60(8): 652-660. [10] Nguyen B, Miah S. Analysis of Maritime Air Defence Scenarios[R]. Ottawa: Defence Research and Development Canada, 2014. (责任编辑:尚彩娟) Analysis and Calculation of Defense Efficiency in Multiple Shooting Mode LI Long-yue, LIU Fu-xian, ZHAO Hui-zhen (Air and Missile Defense College, Air Force Engineering University, Xi’an 710051, China) Considering the shooting process of the red (defensive side) shooting the blue (offensive side), a calculation method of interceptor allocation and Effectiveness of Defense (ED) in multishooting mode is proposed. Firstly, for shoot-shoot strategy, the interceptors’allocation method to gain maximum effectiveness of defense is proposed under given number of red interceptors and blue targets. Secondly, for salvo-look-salvo strategy, in consideration of the factors such as shooting times and salvo size, the iterative recursive generation method is given for multi shooting ED of the red. The simulation examples are carried out to verify the method of interceptor allocation and ED, and the inherent law is discussed. shooting mode; salvo-look-salvo; effectiveness of defense; generating function 1672-1497(2016)05-0050-04 2016-07-18 全军军事类研究生课题 李龙跃(1988-),男,博士研究生。 E83 A 10.3969/j.issn.1672-1497.2016.05.0102 “齐射—观察—齐射”策略
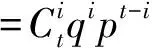
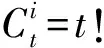

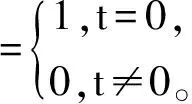
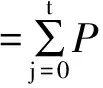






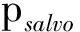
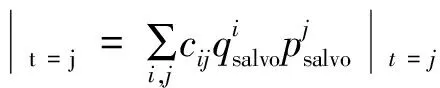
3 实例仿真

4 结论

