基于短时加权峰度的信号冲击特征提取
樊新海, 张传清, 刘相波, 张丽霞
(装甲兵工程学院机械工程系, 北京 100072)
基于短时加权峰度的信号冲击特征提取
樊新海, 张传清, 刘相波, 张丽霞
(装甲兵工程学院机械工程系, 北京 100072)
针对机械故障诊断中信号冲击特征的提取问题,提出了加权峰度这一新的幅域特征参数。结合某型变速箱断齿故障振动信号,采用短时处理方法对比分析了加权峰度和传统峰度对信号冲击特征提取的应用效果。研究结果表明:合理选择短时窗的宽度,通过逐点滑动得到短时加权峰度,能够反映出信号中的冲击特征,再应用频谱细化技术可以有效地得到冲击成分的频域信息。
故障诊断; 信号处理; 冲击特征提取; 加权峰度; 短时处理
机械出现故障时常伴有冲击现象产生,在实测振动信号中出现或强或弱、或持续存在或断续存在的冲击成分。有效地提取这些冲击特征,并结合频谱细化分析来推断冲击产生的根源部位是实现故障辨识和定位的常用方法之一[1-2]。峰度作为一种幅域特征参数,可用来反映信号概率密度分布的情况,在统计分析中具有重要的地位。基于此,笔者定义了加权峰度这一新的幅域特征参数,结合某型坦克变速箱断齿故障振动信号,利用短时处理方法提取局部加权峰度来反映信号的冲击特征,取得了较好的应用效果。加权峰度依据信号自身特点具有较好的自适应性和平滑作用,既保持了对信号冲击特征的敏感性,又提高了稳定性。
1 加权峰度
峰度是表征随机变量X(t)非高斯性的一种测度[3],主要有以下2种定义方式:
Ku1=E(X-EX)4-3[E(X-EX)2]2;
(1)
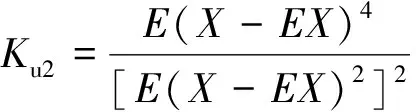
(2)
式(1)是有量纲的,而式(2)是无量纲的。
按照式(1)定义,高斯分布的峰度为0,据此可将随机变量X(t)分为高斯型(Ku1=0)和非高斯型(Ku1≠0)。非高斯型随机变量又可分为超高斯型(Ku1>0)和亚高斯型(Ku1<0)。与高斯型随机变量相比,超高斯型随机变量分布范围较宽,在均值附近有显著尖峰,在偏离均值的两边有拖尾;而亚高斯型随机变量分布范围较窄,在均值附近没有显著尖峰,分布比较均匀。
按照式(2)定义,高斯分布的峰度为3,则超高斯型分布Ku2>3,亚高斯型分布Ku2<3,也可将式(2)改写为
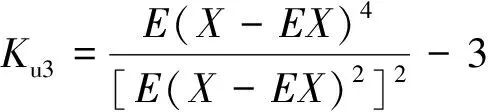
(3)
使得高斯分布的峰度为0,超高斯型分布Ku3>0,亚高斯型分布Ku3<0。
不论采用何种定义方式,都可用峰度来定量表征一个随机变量分布的尖峰程度或偏离高斯分布的程度。由于MATLAB采用了式(2)的定义方式,因此本文也采用该定义方式。
在峰度的定义中,E(X-EX)4为X(t)的4阶中心矩,E(X-EX)2为X(t)的2阶中心矩,亦即方差。笔者在此定义一个新的幅域特征参数:X(t)的4阶中心矩与2阶中心矩之比,即

(4)
Ku4虽然是一种比值定义方式,但它是有量纲的。Ku4也可理解为对峰度Ku2进行加权,权值就是方差,本文称其为加权峰度。
2 短时处理
冲击信号往往表现为幅值突然增大后急剧振荡衰减,具有明显的非高斯特性。当一个平稳信号中含有间歇性冲击成分时,在存在冲击的时段与不存在冲击的时段,其幅域特征参数均会有一定变化,因此利用信号短时处理方法可反映出其变化情况[4]。
短时处理方法就是用一个短时窗w(t)对x(t)进行截断,得到信号xw(t)=x(t)w(t),计算xw(t)的幅域特征参数,此时该参数是由窗口内的信号计算所得,而与窗口外的部分无关,因此短时幅域特征参数反映了信号局部分布特性[5]。再通过移动窗重复上述过程,就可得到不同时段的短时幅域特征参数。本文对峰度和加权峰度进行短时处理的具体算法如下:
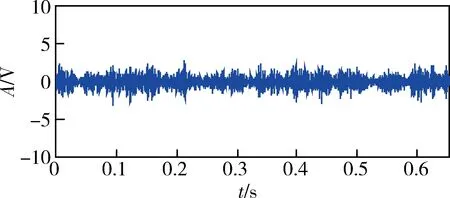
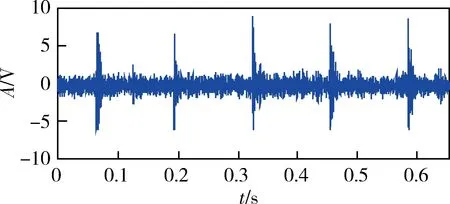
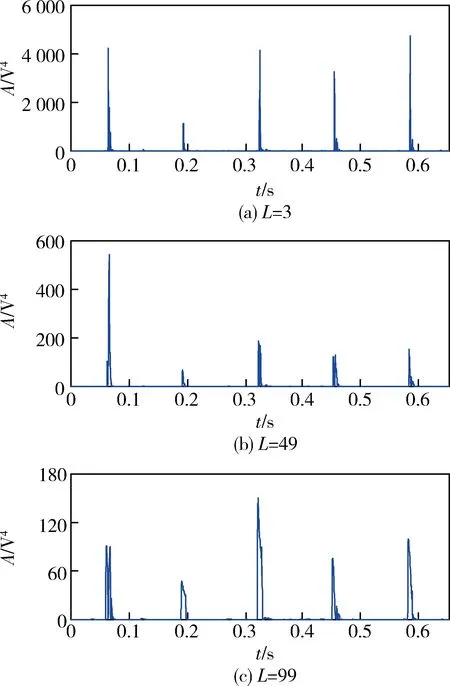
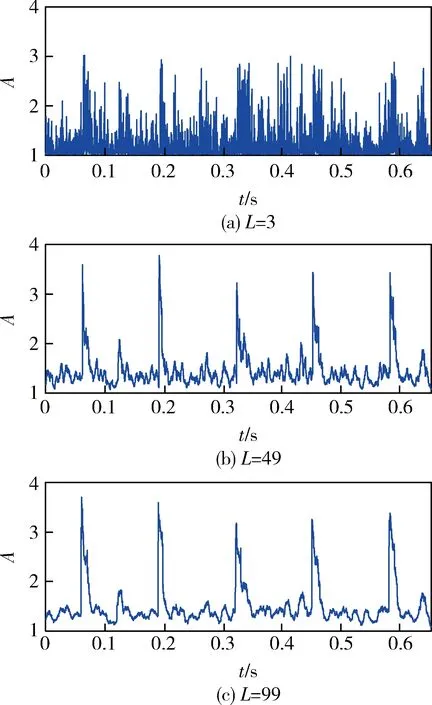
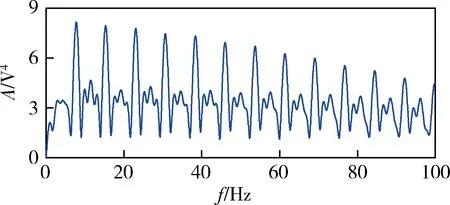
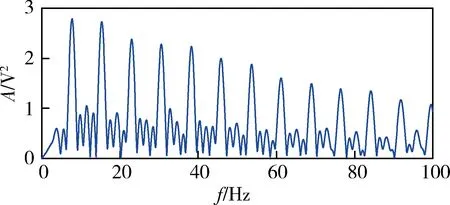
对于长时间序列x(n),n=0,1,…,N-1,利用长度为L(L xm(l)=x(m+l), l=0,1,…,L-1,m=0,1,…,N-L。 其均值为 然后,按照式(1)、(2)计算xm(l)的峰度: (5) (6) 为了避免Ku1(m)<0,通常取其绝对值|Ku1(m)|。按照式(4)计算xm(l)的加权峰度: (7) L为窗宽,即计算每小段信号峰度和加权峰度时的点数,短时峰度和短时加权峰度序列的点数将变为N-L+1,为了便于后续处理,使之也具有N点,可先在x(n)两端分别补L/2个0。 由于短时矩形窗是逐点滑动的,原信号中的冲击特征会在短时峰度和短时加权峰度序列的幅值变化中体现出来,并且冲击发生的时刻得到保留。 将某型坦克变速箱主轴上的3挡被动齿轮锯断,在实车上模拟了断齿故障,测取了断齿前后发动机在低速(不超过700 r/min)、平坦水泥路、3挡平稳直驶时的发动机曲轴转速和变速箱箱体振动加速度信号。图1、2分别为正常状态和断齿时变速箱垂直方向的振动信号。 图1 正常时变速箱垂直方向的振动信号 图2 断齿时变速箱垂直方向的振动信号 对比图1、2可见:断齿时振动信号中明显存在周期性较强的大幅值冲击。为判断这种冲击是否由断齿齿轮啮合产生,需提取信号中的冲击特征以及确定冲击出现的频率信息。 3.1 时域对比 在对信号进行短时处理时,L取值很重要,但也没有明确的选择依据。从图2来看,一次大幅值冲击从出现到消失约为99点,即当L=99时,矩形窗基本可以覆盖一个完整的冲击持续时间。在此选择3种不同的窗宽进行对比分析,即L=3,49,99,利用式(5)-(7)分别计算有量纲短时峰度Ku1(m)、无量纲短时峰度Ku2(m)和有量纲短时加权峰度Ku4(m),结果分别如图3-5所示。 由图3可见:Ku1(m)对冲击成分的敏感性较强,L≥2即可将冲击特征反映出来;但不同时段的冲击最大幅值差异较大,在一些冲击处还出现了冲击分裂现象,即由一个冲击变成几个更短暂的冲击;随着L增大,Ku1(m)幅值呈减小趋势。 图3 断齿振动信号的Ku1(m) 图4 断齿振动信号的Ku2(m) 图5 断齿振动信号的Ku4(m) 由图4可见:Ku2(m)对冲击成分的敏感性较弱,L过小时,将无法反映信号中的冲击特征;随着L的增大,信号中的冲击特征逐渐得到较好的体现,但同一冲击内仍存在较大的局部波动,“毛刺”严重;Ku2(m)取值总体稳定,随L变化不大。 由图5可见:Ku4(m)对冲击成分的敏感性和稳定性均较好,L在一定范围内变化都可将冲击特征反映出来;同时,不同冲击的幅值波动较小,波形更为光滑。 因此,从时域综合性能来看,三者之中加权峰度Ku4(m)对大幅值的冲击特征反映最好。其原因是:Ku4(m)以信号自身方差为权重,具有依据信号本身变化自适应性的特点,也具有较好的局部平滑能力,改善了Ku1(m)所提取冲击最大幅值差异较大以及存在冲击分裂等缺点,在保持对信号冲击特征敏感性的同时,又提高了稳定性。 3.2 频域对比 从时域来看,通过合理选择L,短时峰度和短时加权峰度都可以反映出信号的冲击特征。这种冲击出现时间间隔较大,冲击基频较低,而原信号的采样频率较高,如果直接进行离散傅里叶变换,冲击成分频率主要集中在低频区,受频谱分辨率的限制,有时还很难辨识,此时利用频谱细化技术可以更加细致地观察这种冲击成分的频域特点[6]。 利用线性调频Z变换法对图3(b)、4(b)、5(b)所示信号在0~100 Hz频率范围进行细化分析,细化幅值谱分别如图6-8所示。 图6 Ku1(m)的细化幅值谱 图7 Ku2(m)的细化幅值谱 图8 Ku4(m)的细化幅值谱 由图6-8可见:3个频谱都呈现出一定的谐波特性,谐波频率是以7.73 Hz为基频的整倍数变化,谐波幅度总体趋势随谐波次数增大而减小。笔者通过与计算出的断齿齿轮公转频率进行对比,发现二者一致,由此可以断定这种周期性冲击信号是由齿轮啮合过程断齿产生的冲击振动引起的,断齿齿轮每转1周,较大幅值的冲击就会出现1次。但图7所示信号的谐波特性明显不如图6、8,而图6所示信号中其他频率成分明显多于图8。因此,从频域来看,三者之中Ku4(m)应用效果最好。 对于存在大幅值冲击成分的信号,一般取L≥2,利用Ku1(m)和Ku4(m)即可将信号中的冲击特征提取出来,但若L太小,则Ku1(m)容易出现冲击分裂现象;增大L,冲击分裂现象会得到改善,但L取值一般不超过原信号中冲击持续的长度。对于Ku2(m),L需要具有较长的长度。从本文中对某型坦克变速箱断齿振动信号处理结果来看,Ku4(m)的应用效果最好,但未必对任何信号都具有普遍适用性,在实际应用中可根据具体信号特点进行对比分析后选用。 [1] 郭远晶,魏燕定,周晓军,等.基于S变换谱阈值去噪的冲击特征提取方法[J].振动与冲击,2014,33(21):44-50. [2] 高洪波,李允公,于良会,等.基于Gammatone滤波器组的齿轮系统侧隙诱发冲击特征提取[J].机械传动,2015,39(3):23-26. [3] 张晓冉.峰度统计意义的探讨[J].燕山大学学报,2006, 30(1):57-60. [4] 杨富春,周晓军,张志刚.滑动峰态算法的信号弱冲击特征提取及应用[J].振动与冲击,2009,28(4):103-105. [5] 朱利民,钟秉林,贾民平.振动信号短时分析方法及在机械故障诊断中的应用[J].振动工程学报,2000,13(3):400-405. [6] 樊新海,曾兴祥,张丽霞,等.基于CZT的频谱细化算法及应用[J].装甲兵工程学院学报,2012,26(1):59-62. (责任编辑: 尚彩娟) Signal Impact Feature Extraction Based on Short-time Weighted Kurtosis FAN Xin-hai, ZHANG Chuan-qing, LIU Xiang-bo, ZHANG Li-xia (Department of Mechanical Engineering, Academy of Armored Force Engineering, Beijing 100072, China) In view of signal impact feature extraction in machinery fault diagnosis, a new amplitude domain feature parameter named weighted kurtosis is put forward in this paper. Combining certain gearbox broken teeth failure vibration signal, application effects of weighted kurtosis and traditional kurtosis on signal impact feature extraction are analyzed contrastively by short-time processing method. The study result shows that the short-time weighted kurtosis can reflect the features of impact signal by choosing the width of short-time window reasonably and sliding point by point, and the frequency domain information of impact component can be acquired using spectrum zoom technique. fault diagnosis; signal processing; impact feature extraction; weighted kurtosis; short-time processing 1672-1497(2016)05-0073-04 2016-02-26 樊新海(1973-),男,副教授,博士。 TP206+.3 A 10.3969/j.issn.1672-1497.2016.05.015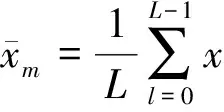
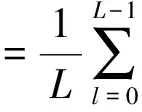
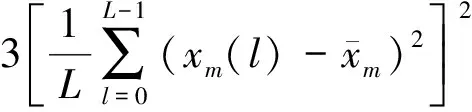
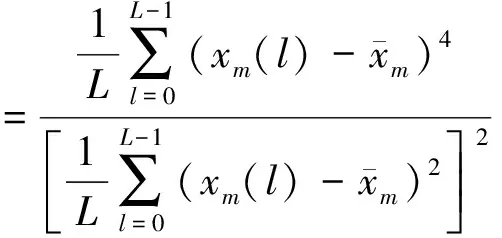
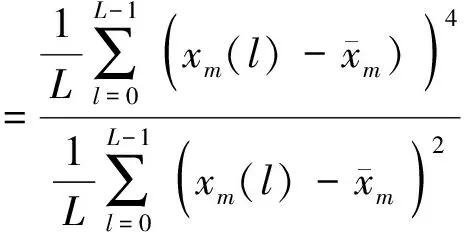
3 对比分析


4 结论

