Cu/Zr纳米多层膜的力学性能及塑性变形行为

刘贵民， 王 尧， 朱晓莹， 杜 军

(装甲兵工程学院装备维修与再制造工程系， 北京 100072)

Cu/Zr纳米多层膜的力学性能及塑性变形行为

刘贵民， 王 尧， 朱晓莹， 杜 军

(装甲兵工程学院装备维修与再制造工程系， 北京 100072)

为研究Cu/Zr纳米多层膜的力学性能及塑性变形行为，采用磁控溅射方法制备了调制比为1，调制周期Λ=12，20，40 nm的Cu/Zr纳米多层膜，利用X射线衍射(X-Ray Diffraction, XRD)和扫描电子显微镜(Scanning Electron Microscopy，SEM)对纳米多层膜的晶体结构和截面形貌进行了表征，利用纳米压痕仪在0.01、0.03、0.05、0.1、0.2、0.5 s-1等应变率下采用连续刚度法测量了多层膜的硬度。结果表明：不同调制周期结构的Cu/Zr纳米多层膜结晶性良好；Λ=12，20，40 nm的Cu/Zr纳米多层膜的强度(H/2.7)分别为1.90、1.83、0.80 GPa，Cu/Zr纳米多层膜的强度随调制周期的减小而增大，其塑性变形机制在调制周期减小到20 nm后由位错单层滑移机制转变为位错穿越界面运动机制；Λ=12，20，40 nm的Cu/Zr纳米多层膜的应变率敏感指数m分别为0.042、0.033、0.025，Cu/Zr纳米多层膜的应变率敏感指数随调制周期的减小而增大，这可能是由调制周期减小导致的晶粒尺寸减小和非共格界面密度的增大引起的。

Cu/Zr纳米多层膜； 调制周期； 强度； 应变率敏感性； 变形机制

金属纳米多层膜广泛应用于微电子器件中，特别是微电子机械系统(Micro Electro Mechanical Systems,MEMS)的兴起和发展对纳米多层膜的力学性能及服役行为提出了更高的要求[1]。国内外研究者已对Cu/Zr多层膜体系做了大量的研究，但大都关注硬度、弹性模量、屈服强度、延性、断裂韧性等力学性能与调制周期的关系。近年来，纳米晶体金属材料在应变率改变条件下的塑性变形行为受到了人们的关注，研究人员对纳米金属材料的应变率敏感性进行了大量的试验研究，然而对纳米多层膜体系的应变率敏感性研究较少。应变率敏感性指塑性变形时材料的流变应力对应变率的敏感性，即当应变率增大时材料的强化倾向的参数[2]，其是研究材料变形机制的一个重要的力学性能参数。深入研究纳米多层膜的变形机制对提升薄膜的力学性能、设计开发高力学性能的纳米多层膜体系具有指导意义[3-4]。

Cu/Zr纳米多层膜每相邻2个层形成一个周期，称为调制周期，用Λ来表示，Λ=hCu+hZr，其中hCu和hZr分别为纳米多层膜组元Cu和Zr的厚度，调制比η=hCu/hZr。当调制周期尺寸减小到纳米量级时，高的界面密度成为纳米多层膜的结构特征，两相界面作为位错源与位错运动的障碍，扮演着与晶界相似的角色，成为影响纳米多层膜力学性能和塑性变形机制的关键因素之一[5]。Cu/Zr多层膜具有fcc/hcp的非共格界面结构，研究应变率敏感性随Cu/Zr纳米多层膜调制周期的变化规律，有助于深入了解纳米多层膜的塑性变形机理，特别是界面结构对其塑性变形机理的影响。

磁控溅射是一种常用的制备金属纳米多层薄膜的物理气相沉积技术，所制备的薄膜具有纯度高、致密性好和成膜均匀等特点，可制备有特定取向的沉积态纳米晶结构多层膜。笔者将通过强度、应变率敏感性来探讨磁控溅射方法制备的沉积态Cu/Zr纳米多层膜的力学性能及塑性变形行为。

1 实验部分

1.1 样品的制备和表征

利用AS500DMTXB型非平衡磁控溅射离子镀设备制备Cu/Zr纳米多层膜，其靶材为纯度均为99.99%的Cu和Zr，基体材料为Si<100>基片。

首先将基片在丙酮中超声清洗10 min，然后用去离子水超声清洗10 min，最后用氮气吹干，立刻放入真空室进行镀覆，其真空预抽至5×10-4Pa。镀层沉积时，氩气流量控制为15.0 mL/min，溅射气压保持在0.5 Pa，交替启动Zr靶和Cu靶，通过控制镀膜时间来确保单层Zr膜和Cu膜的厚度相等。靶与基片间距为60.0 mm，溅射时基片自转设定在10 rad/min，每次实验前进行10 min的预溅射以除去靶表层的氧化物，样品总厚度控制在500 nm左右。

利用日本理学生产的D/max-rB转靶X射线衍射仪(X-Ray Diffraction, XRD)进行纳米多层膜晶体结构分析，CuKα为特征X射线，入射波长为0.154 nm，管电压为40 kV，管电流为120 mA。利用Nava Nano SEM450/650场发射型超高分辨率扫描电镜(Scanning Electron Microscopy, SEM)表征纳米多层膜截面形貌。采用Nano-Test 600型纳米压痕仪进行纳米压痕实验，其最大压入深度为450 nm，应变率为0.01、0.03、0.05、0.1、0.2、0.5 s-1，每个应变率下采样点为5个，结果取平均值[6]。

1.2 强度的计算方法

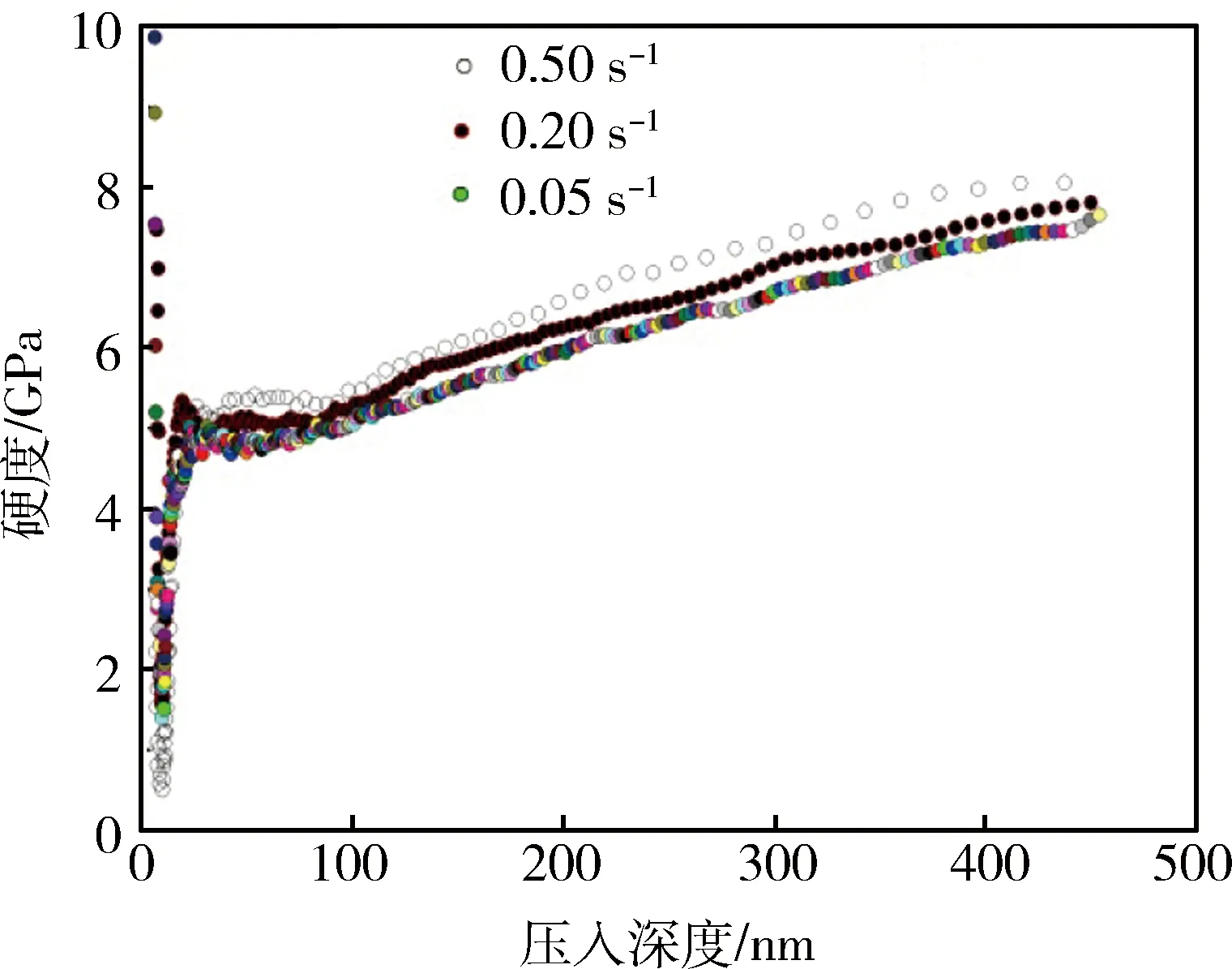
图1 不同应变率下Cu/Zr多层膜的硬度值随压入深度变化曲线

纳米压痕实验能获取薄膜硬度值，但很多研究多层膜形变机理的模型都是根据强度进行分析，多层膜的强度通常可认为是使位错开始运动所需要的最小应力，笔者按照H/2.7[7]的规则将测试所得硬度H换算成强度，以便于研究其形变机理。为排除基体的影响，纳米多层膜硬度按照样品总厚度(500 nm左右)的1/10～1/7规则进行计算。图1为不同应变率下Cu/Zr多层膜硬度值随压入深度的变化曲线。可以看出：压入深度在70～450 nm范围内硬度测量值升高，说明随压入深度增加，硬度测量值受到基体的影响；压入深度在40～70 nm范围内硬度测试值随调制周期变化出现平台，表明此压入深度范围内测试获得的硬度不受基体影响，选取此范围内的硬度测试平均值与真实硬度值接近。

2 结果与分析

2.1 结构与形貌

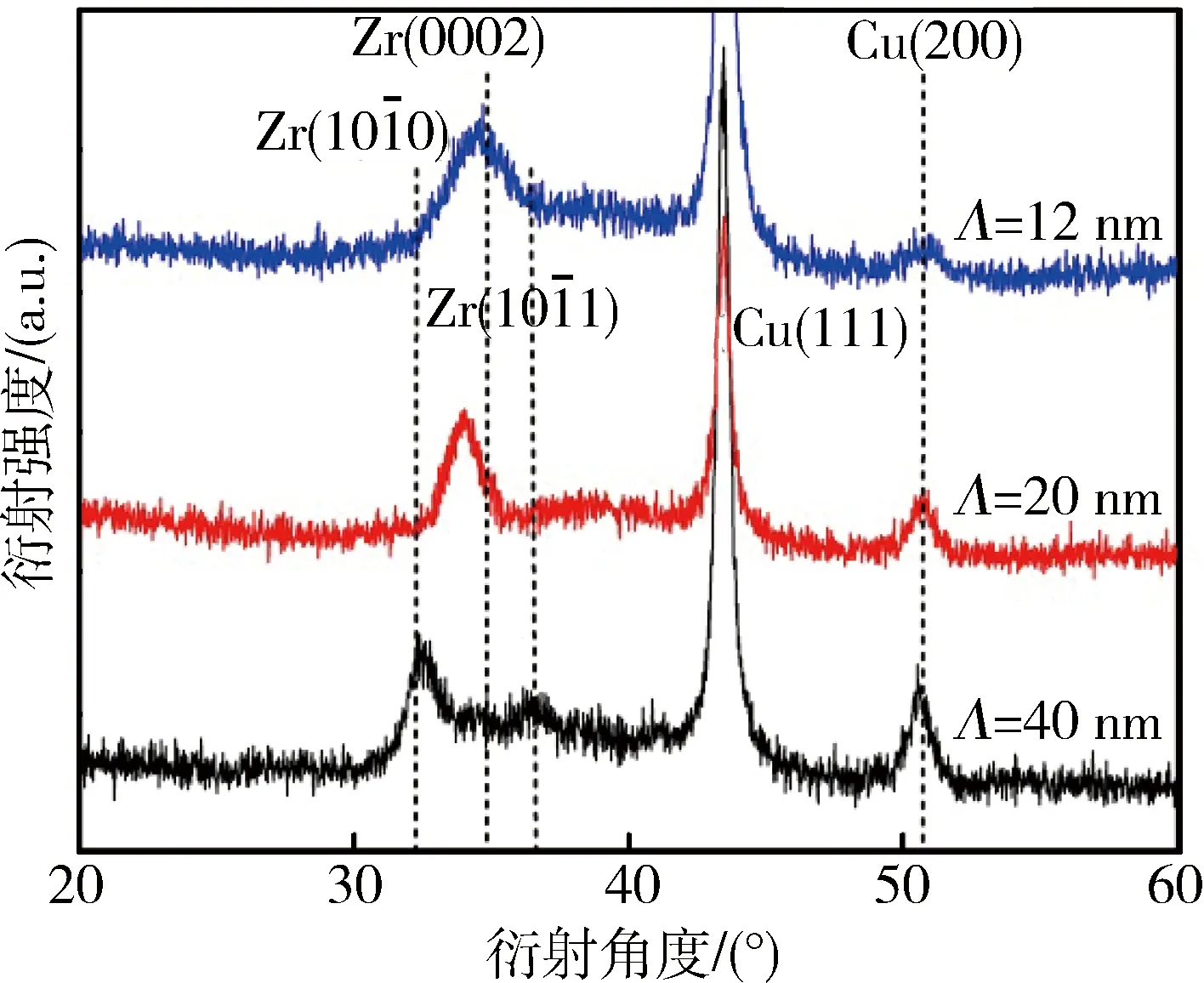
图2 不同调制周期Cu/Zr纳米多层膜的XRD图谱

金属纳米多层膜异质界面属于何种界面结构主要取决于晶体结构和组元间的晶格错配度ζ，即

ζ=(aA-aB)/(aA+aB)，

(1)

式中：aA和aB分别为纳米多层膜A和B的晶格常数。ζCu/Zr=11.2%，晶格错配度较大，且Cu/Zr界面结构为fcc/hcp结构，晶体结构不同，因此本文Cu/Zr多层膜界面属于非共格结构[10]。

图3为不同调制周期的Cu/Zr纳米多层膜SEM截面图。从图3(a)可以看出：Λ=40 nm的Cu/Zr多层膜未观察到清晰的分层现象，多层膜的总厚度为530 nm。从图3(b)可以看出:Λ=20 nm的Cu/Zr多层膜观察到了分层现象，多层膜总厚度为510 nm。出现上述现象的原因为：由于Si基体的薄膜材料截面样品制备通常采用直接折断的方法，因此断裂方式对断口形貌有较大影响，Cu/Zr多层膜有良好的塑性，多层膜塑性断裂后在SEM下可能观察不到分层现象[11]。

图3 不同调制周期的Cu/Zr纳米多层膜SEM截面图

2.2 力学性能与变形机理

图4为应变率0.05 s-1下不同调制周期的Cu/Zr纳米多层膜的强度实验值与模型拟合值，σCu=0.78 GPa，σZr=1.2 GPa，则按照复合材料混合规则计算，Cu/Zr纳米多层膜强度的平均值σROM=(σCu+σZr)/2=0.99 GPa，如图4中箭头标示。由图4可以看出：当Λ=40 nm时，多层膜的强度值为0.8 GPa，与多层膜强度平均值近似；但随着调制周期由40 nm减小到12 nm，纳米多层膜的强度明显提高，由0.80 GPa增大到了1.90 GPa，表现出了强化效应[12]。

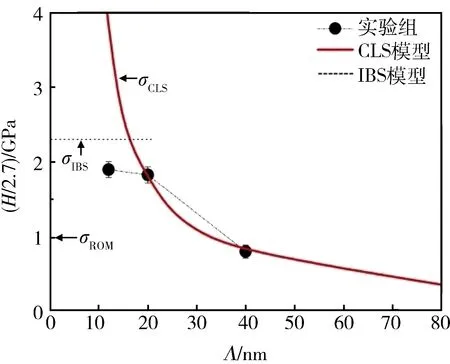
图4 应变率0.05 s-1下不同调制周期的Cu/Zr纳米多层膜的强度实验值与模型拟合

2.2.1 CLS模型

近20年的研究表明：当调制周期在亚微米到微米量级(也有学者认为是调制周期大于40 nm)时，界面可以等同于晶界对位错运动起钉扎作用，此时纳米多层膜的强化机制为位错在界面处的塞积，纳米多层膜强度(或硬度)与调制周期的关系符合Hall-Petch公式[13]。当调制周期下降到几十纳米到几纳米之间时，由于纳米多层膜层内位错密度太小，界面处产生的应力集中无法使位错穿越界面，Hall-Patch理论已不能解释强化现象，这时变形机制符合单个位错在层内滑移模型或CLS模型[14]。纳米多层膜的强度计算公式为

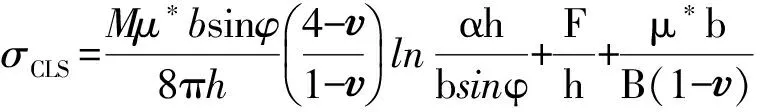
(2)

式中：M=3.06，为泰勒常数；b为柏氏矢量，其中bCu=0.25 nm[15]；α为位错芯部区域的常数，在Cu/X多层膜体系中，对于Cu/Cr与Cu/Zr，α=0.2[16]；Cu= 0.34[17]，为泊松比；F/h为界面弹性变形造成的界面应力，B为不滑移位错之间的距离，两者作为常数经拟合得到；φ=70.5°，为滑移面与界面所成角度；μ*=μCu·μZr/(2VCu·μCu+2VZr·μZr)，为Cu和Zr的平均剪切模量，其中μCu=45 GPa，μZr=33 GPa[16],VCu与VZr分别为Cu和Zr的体积分数。

根据式(2)可得CLS模型的拟合曲线，如图4中实线所示。

拟合结果为：F=17.4 J/m2，B=14.8 nm，如果位错滑移引起的面内应变ε由滑移过程中在界面上形成的不滑移位错协调，则满足B=b/ε，当b=0.25 nm,B=14.8 nm时，ε=1.7%。Misra等[18]指出:选取1%～2%的塑性应变时，根据CLS模型计算所得流变应力能够很好地吻合强度数值。这说明此处拟合得到B=14.8 nm是合理的。

由图4可以看出：Cu/Zr纳米多层膜强度在Λ=20,40 nm时采用CLS模型拟合较好，而在Λ=12 nm时则远远偏离CLS模型拟合值。这表明：随着调制周期减小，Cu/Zr纳米多层膜的塑性变形机制发生了转变，不再符合位错约束层滑移机制。大量研究表明：当调制周期下降到某个临界值以下时，位错在单层膜内滑移所需要的最小外应力要大于位错穿越界面所需要的应力，此时纳米多层膜的塑性变形机制将转变为位错穿越界面机制，纳米多层膜的强度趋近于界面强度。

2.2.2 IBS模型

Misra等[18]摆出纳米多层膜的峰值强度/硬度是由单根位错穿过界面所需应力决定的，界面对位错滑移运动的阻力由界面结构决定。纳米多层膜具有共格界面、半共格界面以及非共格界面3种界面结构，其中：非共格界面的纳米多层膜的界面强度取决于组元材料间的模量失配以及失配位错与界面的相互作用。根据2.1节的分析结果可知：Cu/Zr纳米多层膜具有非共格界面，因此可利用界面强度模型(Interfacial Bonding Strongth，IBS)估算具有非共格界面结构的Cu/Zr纳米多层膜在小调制周期的强度σIBS[19-20]，σIBS的计算公式为

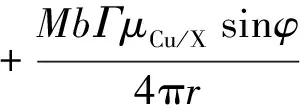
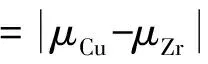
根据IBS模型计算出Cu/Zr纳米多层膜界面理论强度为2.37 GPa，如图4中虚线所示。可以看出：与Λ=12 nm的Cu/Zr纳米多层膜的强度测量值1.89 GPa相比，IBS模型计算值略高。这是由于随着调制周期减小，少量的Cu固溶入Zr晶格中，使得Cu/Zr不能形成完全清晰的界面，界面位错缺陷的增加导致滑移位错更容易在界面上通过位错反应穿越界面，从而使实际界面强度比IBS模型中计算的数值要低。

2.3 应变率敏感性

图5 Λ=20 nm的Cu/Zr纳米多层膜在不同应变率下的压入深度-载荷曲线

图5为Λ=20 nm的Cu/Zr纳米多层膜在不同应变率下的压入深度-载荷曲线。可以看出：随着应变率的增大，达到相同的压入深度需要的载荷也增加，表明Cu/Zr纳米多层膜的硬度对应变率具有敏感性，这与纳米晶金属Ti的应变率敏感性实验中得到的结果相似[21]。

图6为不同调制周期和应变率下Cu/Zr纳米多层膜的硬度，可以看出：不同调制周期的Cu/Zr纳米多层膜硬度随应变率增大均出现了不同程度的提升。

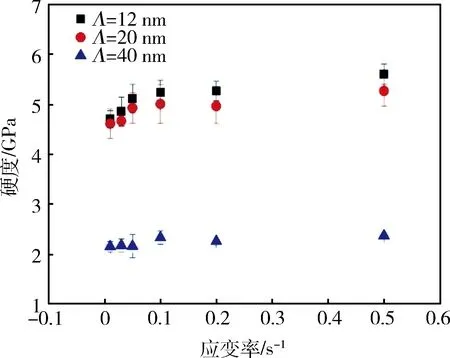
图6 不同调制周期和应变率下Cu/Zr纳米多层膜的硬度

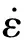
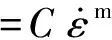
(4)

式中：m为应变率敏感性指数，也是材料随应变率改变的硬化指数，其值越大，说明发生相同应变量所需要的应力越大。用H代替σ，对等式两边做双对数变换后可得

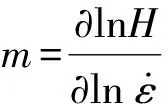
(5)

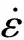
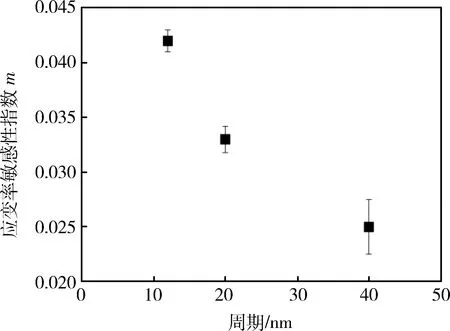
图7 不同调制周期Cu/Zr纳米多层膜的应变率敏感指数

3 结论

采用磁控溅射法制备了不同调制周期的Cu/Zr纳米多层膜，讨论了Cu/Zr多层膜的硬度、强度和应变率敏感性，并对应变率敏感性随调制周期的变化特点进行了深入分析。结果表明：随着调制周期减小，Cu/Zr多层膜的硬度、强度和应变率敏感性逐渐增大，这为提升Cu/Zr多层膜综合力学性能提供了一种可行的方法。下一步，将对更小调制周期的Cu/Zr多层膜力学性能进行研究。

[1] Dehm G. Miniaturized Single-crystalline FCC Metals Deformed in Tension: New Insights in Size-dependent Plasticity[J]. Progress in Materials Science, 2009, 54(6): 664-688.

[2] 谢子令, 武晓雷, 洪友士. 微纳米晶金属的应变率敏感性及应变硬化行为分析[J]. 固体力学学报, 2007, 28(1):43-48.

[3] 张文勇, 孙德恩, 裴晨蕊, 等. 调制周期对CrAlN/ZrN纳米多层膜韧性的影响[J]. 表面技术, 2016, 45(1): 55-61.

[4] 顾超, 朱宏喜, 任凤章, 等. 双槽电沉积法制备Cu/Ag纳米多层膜[J]. 表面技术, 2011, 40(4):4-7.

[5] Huang P, Wang F, Xu M, et al. Strain Rate Sensitivity of Un-equal Grained Nano-multilayer[J]. Materials Science and Engineering A, 2011, 528(18):5908-5913.

[6] 龙东平, 薛建荣, 晏智鑫. 纳米压痕和划痕法测定TiO2纳米薄膜的力学性能[J]. 表面技术, 2015, 44(6): 115-119.

[7] 朱晓莹. 若干金属纳米纳米多层膜界面结构及力学性能研究[D]. 北京: 清华大学, 2010.

[8] 关志良. Cu/Zr和Cu/Ta纳米多层膜的制备与电/力学性能研究[D]. 西安： 西安理工大学, 2012.

[9] 曹峻. TiVCN复合膜与TiN/VCN, TiCN/VCN多层膜的性能研究[D]. 镇江： 江苏科技大学, 2012.

[10] 魏明真. 金属多层膜微观结构与力学性能的尺度效应[D]. 南京： 南京大学， 2015.

[11] 文胜平. 若干金属多层膜的微结构及力学性能研究[D]. 北京： 清华大学, 2007.

[12] Hang J Y, Li J, Liang X Q, et al. Achieving Optimum Mechanical Performance in Metallic Nanolayered Cu/X(X=Zr, Cr) Micropillars[J]. Scientific Reports, 2014, 4(3): 528-536.

[13] Carlton C E, Ferreira P J. What is behind the Inverse Hall-Petch Effect in Nanocrystalline Materials[J]. Acta Materialia, 2007, 55(11): 3749-3756.

[14] Abdolrahim N, Zbib H M, Bahr D F. Multiscale Modeling and Simulation of Deformation in Nanoscale Metallic Multilayer Systems[J]. International Journal of Plasticity, 2014, 52: 33-50.

[15] 张金钰. 金属多层膜力学行为及其组元与尺寸效应[D]. 西安： 西安交通大学, 2011.

[16] Zhang J Y, Liu Y, Chen J, et al. Mechanical Properties of Crystalline Cu/Zr and Crystalamorphous Cu/Cu-Zr Multilayers[J]. Materials Science & Engineering: A, 2012, 552(34): 392-398.

[17] Zhang J Y, Zhang X, Liu G, et al. Scaling of the Ductility with Yield Strength in Nanostructured Cu/Cr Multilayer Films[J]. Scripta Materialia, 2010, 63(1): 101-104.

[18] Misra A, Hirth J P, Hoagland R G. Length-scale-dependent Deformation Mechanisms in Incoherent Metallic Multilayered Composites[J]. Acta Materialia, 2005, 53(18): 4817-4824.

[19] Niu J J, Zhang J Y, Liu G, et al. Size-dependent Deformation Mechanisms and Strain-rate Sensitivity in Nanostructured Cu/X (X=Cr, Zr) Multilayer Films[J]. Acta Materialia, 2012, 60(9): 3677-3689.

[20] Mara N A, Misra A, Hoagland R G, et al. High-temperature Mechanical Behavior/Microstructure Correlation of Cu/Nb Nanoscale Multilayers[J]. Materials Science and Engineering: A, 2008, 493(1): 274-282.

[21] Wang J L, Yang Z. Orientation-dependent Hardness in As-Deposited and Low-temperature Annealed Ti/Ni Multilayer Thin Films[J]. Journal of Applied Mechanics, 2015, 82(1): 1008-1016.

[22] Zhou Q, Li J J, Wang F, et al. Strain Rate Sensitivity of Cu/Ta Multilayered Films: Comparison between Grain Boundary and Heterophase Interface[J]. Scripta Materialia, 2016, 111:123-126.

[23] Zhang J Y, Wang Y Q, Wu K, et al. Strain Rate Sensitivity of Nanolayered Cu/X(X=Cr, Zr) Micro-pillars: Effects of He-terophase Interface/twin Boundary[J]. Materials Science & Engineering: A, 2014, 612(33): 28-40.

[24] Huang P, Wang F, Xu M. Dependence of Strain Rate Sensitivity upon Deformed Microstructures in Nanocrystalline Cu[J]. Acta Materialia, 2010, 58(15): 5196-5205.

[25] 王岩. Fe注入α-A12O3、CO注入单晶硅注入态与退火态的微结构研究[D]. 大连： 大连理工大学, 2008.

(责任编辑:尚菲菲)

Mechanical Properties and Plastic Deformation Behavior of Cu/Zr Nanoscale Multilayer Films

LIU Gui-min, WANG Yao, ZHU Xiao-ying, DU Jun

(Department of Equipment Remanufacture Engineering, Academy of Armored Force Engineering, Beijing 100072, China)

To investigate the mechanical properties and plastic deformation behavior of Cu/Zr nanoscale multilayer films, Cu/Zr nanoscale multilayer coatings with different modulation periods (Λ=12, 20, 40 nm) are deposited in a magnetron sputtering system, fixing the layer thickness ratio Cu ∶Zr as 1. The microstructure and cross-section fracture morphology are investigated by X-Ray Diffraction (XRD) and Scanning Electron Microscopy (SEM). Hardness tests are conducted using MTS Nanoindenter XP®system under Continuous Stiffness Measurement (CSM) mode over a range of loading strain rates (0.01, 0.03, 0.05, 0.1, 0.2, 0.5 s-1).The Results show that all the multilayers are crystalline in spite of the varying modulation periods. The strength (H/2.7) of Cu/Zr nanoscale multilayers withΛ=12, 20, 40 nm are 1.90,1.83,0.80 GPa, respectively. The strain rate sensitivity values (m) withΛ=12，20，40 nm are 0.042, 0.033 and 0.025, respectively. The strength values of the Cu/Zr nanoscale multilayers increase with the decreasing modulation periods and the transition of the deformation mechanism from confined layer slip to crossing of dislocations across interfaces occurred as the modulation periods decrease down to 20 nm. The strain rate sensitivity values increase with the decreasing modulation period, which can probably be attributed to the smaller crystal size and higher incoherent interface density that caused by decreasing modulation period.

Cu/Zr nanoscale multilayer films; modulation periods; strength; strain rate sensitivity; deformation mechanism

1672-1497(2016)05-0077-05

2016-04-11

国家自然科学基金资助项目(51401238)

刘贵民(1971-)，男，教授，博士。

TG174.444

A

10.3969/j.issn.1672-1497.2016.05.016