作战体系加权网络节点重要度评估

孙成雨， 申卯兴， 王宇峰， 汪 鑫

(空军工程大学防空反导学院， 陕西 西安 710051)

作战体系加权网络节点重要度评估

孙成雨， 申卯兴， 王宇峰， 汪 鑫

(空军工程大学防空反导学院， 陕西 西安 710051)

针对作战体系中各作战实体的重要度评估问题，建立了作战体系加权网络模型，提出了基于拓扑势指标的网络节点重要度评估方法。首先，采用基于模糊偏序关系的多属性决策方法获得节点的属性重要度值；其次，设计基于社团的改进最短路径距离算法，获得节点的交互作用路径及距离；最后，利用拓扑势指标度量评估节点的重要度。通过实例分析验证了改进最短路径距离算法及拓扑势指标的有效性，可进一步为体系的抗毁性研究提供支撑。

节点重要度； 拓扑势； 多属性决策； 加权网络

网络节点重要度评估是网络科学研究中的一个热点[1-3]。传统的节点重要度评估方法主要有基于社会网络分析中“重要性等价于显著性”思想的方法和基于系统科学领域“破坏性等价于重要性”思想的方法，这些方法及其指标多是针对同质节点网络，对于节点具有异质性以及节点作用范围具有局域性的各类作战网络，其具有一定局限性。

作战体系各组成实体具有异质性，其作战单元的重要度主要包括作战单元自身的属性重要度和作战单元在体系网络上的结构重要度[4]。作战单元在作战体系中不同的属性、作战能力使得其具备不同的属性重要度，同时各单元在体系网络结构中因发挥不同的作用而具有不同的结构重要度。卞泓斐等[5]采用灰色关联分析法将节点个体重要度和网络重要度进行了综合；姜志鹏等[6]提出了一种利用节点重要度评价矩阵确定加权网络节点重要度的方法。以上评估方法采用不同的方式融合个体属性和结构属性，采用平均距离、介数等指标度量节点在网络全局的结构重要度。但是，作战体系中各作战实体因受指挥控制、作战协同和情报保障关系的约束而使其作用范围变得有限，全局性的结构指标已不再适用。因此，笔者考虑到节点作用范围的有限性及节点间作用路径的约束特征，设计基于社团的节点最短路径距离算法，利用拓扑势理论融合节点个体属性和网络结构属性，提出基于拓扑势指标的作战体系加权网络节点重要度评估方法。

1 作战体系加权网络

复杂系统由相互作用的众多子系统组成，如果把子系统抽象成节点，把子系统之间的相互作用抽象为节点之间的连边，则复杂系统就可以抽象为复杂网络[7]。作战体系是由各类感知、指控和火力等实体经过不同通信方式连接而成的复杂系统[8]，各实体间存在复杂的交互关系。

定义1：作战体系网络是以作战体系中的感知、指控和火力等实体为节点，以实体间的交互关系为边的网络。

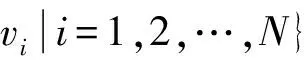
作战体系的物理结构由体系组成实体间的物理连接关系形成，反映各个实体间通过通信网络形成的实际连接情况；作战体系的逻辑结构由实体间的业务处理关系形成，反映了各实体间因业务处理而形成的信息交互情况，基本业务处理关系有情报保障、指挥控制和作战协同关系。因此，获得作战体系网络节点连边集E={E1,E2,E3}，其中：E1为情报保障关系连边集合；E2为指挥控制关系连边集合；E3为作战协同关系连边集合。同时，由于网络连边的属性(业务时延、业务重要程度)多样，因此可建立其连边权值矩阵W。

定义2：作战体系加权网络模型G用四元组表示为

G={V,E,Q,W}。

(1)

根据作战实体的特点提取其属性，可获得Q={q1, q2, q3, q4, q5}，其中：q1为节点对敌威胁程度；q2为节点与作战意图一致度；q3为节点的抗毁能力；q4为节点对我作战影响；q5为节点修复难易度。由于作战实体间的信息传输时延yij∈R+，影响节点业务交互的时效性，因此取其作为网络连边的权值wij，可获得连边权值矩阵W=[wij]N×N，其中

(2)

2 拓扑势理论

在物理学中，场的概念用于描述物质粒子间的非接触相互作用，例如：核子场刻画了核子间的非接触相互作用，场中各点处的势值随距离的增加迅速下降为0[9]。在实际网络中，节点通过连边发生相互作用，由于网络的模块化和社团特性，节点间的相互作用范围有限。因此，拓扑势理论认为：网络节点间的直接或间接关系中存在相互作用，这种作用大小随着网络拓扑距离的增加而迅速衰减。因此，拓扑势理论指出：网络节点拓扑势是节点受自身和近邻节点共同影响所具有的势值[10-11]。

网络的节点集V和连边集E均为非空有限集合，其节点vi的拓扑势[10]为

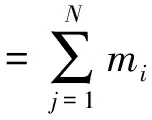
(3)

式中：mi为节点vi的质量、权重等固有属性值；dij为节点vi和vj之间的最短路径距离；σ为影响因子，用于控制节点的影响范围。

3 节点重要度评估

根据节点拓扑势的定义可知：利用节点拓扑势评估作战体系网络节点的重要度，应获得节点的属性值mj以及节点相互影响的最短路径距离dij。

3.1 节点属性重要度

由于基于模糊偏序关系的多属性决策方法可避开权重的问题，不需要提供决策信息表[12]，因此本文采用该方法评估作战体系网络中节点的属性重要度，获得节点的属性值mi，具体步骤如下：

1)确定节点属性集合Q={q1,q2,q3,q4,q5}。

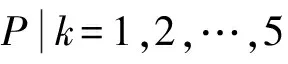
3)获得连续值信息系统。对节点各属性取值进行归一化处理：由于节点的q1、 q2、q3、q4为效益型属性，因此其归一化后的属性值为

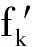
(4)

由于作战体系网络中节点的q5为成本型属性，因此其归一化后的属性值为

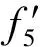
(5)

4)转化为偏序关系模型。在偏序集(V,≤)中，若R为模糊偏序关系，则称关系模型(V,≤,R)为模糊偏序模型，其表达式为

(6)

采用式(6)将评估值模型(V,Q,F′)转化为评估关系模型(V,R)，其模糊偏序关系为

(7)

5)获得网络节点的属性重要度。节点属性重要度的表达式为

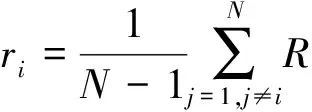
(8)

经过归一化后，可得节点的标准属性重要度为

(9)

3.2 节点间最短路径距离算法

3.2.1 节点交互的最短路径

作战体系网络中节点之间的连边受到作战任务、条令条例、战术战法以及情报保障、作战协同、指挥控制关系的约束，其交互和影响并不是随机和全局的，而是通过指控节点对感知、火力节点的指挥控制实现，具有局部特性。因此，在一定的作战时间、空间内，作战体系网络中各节点间的关系是相对固定的，节点的交互最终会通过指控节点进行。

图1为某舰艇编队防空作战体系加权网络。该舰艇编队中作战实体的性质、属性不同，对应网络节点的属性重要度也不同，其中：v3为战术级指控节点；v13为编队获取空情信息的关键感知节点；v1节点指控的各节点为该防空体系网络中的骨干型装备；v4、v5为编队的骨干火力节点；v2节点指控的各节点为辅助型装备实体，节点间存在多种交互关系。作战实体交互的信息传输时延对应为网络连边的权值。

图1 某舰艇编队防空作战体系加权网络

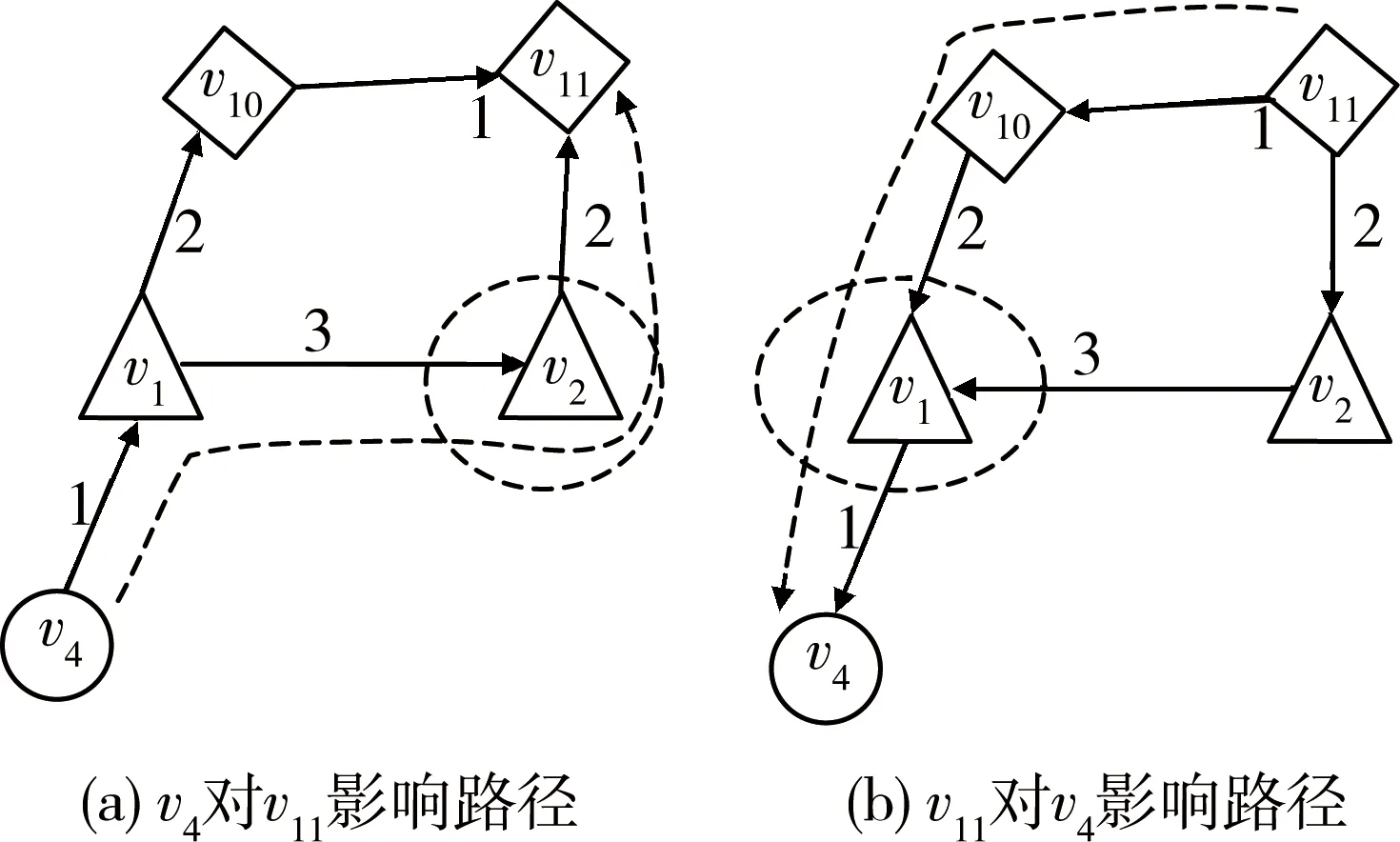
图2 节点v4与v11交互作用的最短路径

图2为节点v4与v11交互作用的最短路径，具体分析过程如下：

1)v4影响v11的最短路径有v4→v1→v10→v11和v4→v1→v2→v11，其中后者符合指控、协同关系。虽然前者的整体时延较短，但v10和v11之间的感知信息交互只实现空情数据的共享，火力节点v4难以通过感知节点影响v11，而是通过指控节点v1和v2的协同实现对v11的影响，因此v4对v11的影响必定通过指控节点v2。

2)v11影响v4的最短路径有v11→v10→v1→v4和v11→v2→v1→v4，二者都符合体系的运行规律和要求，但前者的路径时延最短，因此v11对v4的影响必定通过指控节点v1。

通过以上分析可知：求解节点vi、vj交互的最短路径可转化为求解vi通过某指控节点vc到达vj的最短路径。

3.2.2 指控节点的确定

为求得作战体系网络中节点交互的最短路径距离，首先需要确定指控节点vc，该节点的选择应符合各作战节点的约束关系，为此给出作战体系网络社团的定义。

定义3：在作战体系网络中，包含某指控节点vc及其直接指控的感知、火力节点的部分网络构成一个作战体系网络社团Gc，vc称为该社团的中心节点。

对于任意节点vi、vj，判断节点所在社团及社团中心节点vc。若vi、vj在同一社团中，即vi,vj∈Gc，则dij=dic+dcj，其中指控节点vc是节点vi和vj所在社团的中心；若vi、vj在不同社团中，即vi∈Gc1，vj∈Gc，则dij=dic+dcj，其中指控节点vc只是节点vj所在社团的中心。

3.2.3 算法步骤

在作战体系网络中，节点vi与vj之间的最短路径经过目的节点vj所在社团Gc的指控节点vc，最短路径距离dij=dic+dcj。采用Floyd算法的思想进行改进，设计最短路径距离算法如下：

输入：网络G的连边权值矩阵W。

输出：网络节点间最短路径距离矩阵D。

具体步骤如下：

1)确定各节点所在的社团。以指控节点为中心对网络G进行划分，获得C个社团以及社团节点集合。

2)对于任意节点vi、vj，确定vj所在社团Gc及其中心指控节点vc。

3)对于节点vi、vc，令dic=wic且k=1。

4)更新dic。若dik+dkc

5)令k=k+1，转至步骤4)，直至k=N停止，获得dic。

6)对于节点vc、vj，令dcj=wcj且h=1。

7)更新dcj。若dch+dhj

8)令h=h+1，转至步骤7)，直至h=N停止，获得dcj。

9)由dic和dcj得到dij=dic+dcj。

10)遍历节点vi、vj，获得符合作战约束的最短路径距离矩阵D=[dij]N×N。

3.3 实例分析

3.3.1 节点拓扑势

以图1 所示作战体系加权网络为例，各节点的属性值如表1所示。采用基于模糊偏序关系的多属性决策方法获得节点的属性重要度mi，如表2所示。

表1 作战体系加权网络节点属性值

表2 作战体系加权网络节点的属性重要度

表3 节点拓扑势

3.3.2 节点重要度排序分析

设定节点作用范围l=3，分别基于Floyd算法和改进最短路径距离算法获取节点最短路径，求得节点拓扑势并进行排序，结果分别为v1>v3>v4>v13>v10>v11>v2>v9>v5>v7>v6>v12>v8和v13>v1>v2>v3>v4>v5>v7>v6>v10>v9>v12>v11>v8。

在基于Floyd算法的拓扑势排序中，节点v10、v11的重要度大于节点v2的重要度，分析Floyd算法的基本原理可知：v11、v10和v1、v2是不同社团交互的中继节点，连边(v11,v10)权值小于连边(v1,v2)权值，Floyd算法计算不同社团间节点路径距离较多地选择连边(v11,v10)或(v10,v11)，最终提高了节点v11、v10的结构重要度，使其大于指控节点v2的重要度。同理，感知节点v13的重要度小于火力节点v4的重要度。考虑节点对应作战实体的功能特点和作战信息流动规律，v11、v10的互连只是实现了共享空情信息，并不能传递指控、协同信息，v1、v2才是最终实现指控、协同的节点。可见：Floyd算法在求解最短路径时因忽略了指控、协同关系的约束而存在局限性。

在基于改进最短路径距离算法的拓扑势排序中，v13重要度最高，这是因为v13作为舰艇编队的空情信息来源，直接影响着防空体系作战效能的发挥；v1、v2、v3作为指控节点指控、协同网络中各节点的信息交互，其影响力最大，拓扑势相对较高；v4、v5作为作战体系中骨干型火力系统首先发挥拦截作用，在网络中的影响力同样较大。可见：改进的最短路径距离算法从指控、协同关系出发，通过基于网络社团的最短路径距离算法求解路径，适用于作战体系网络的路径分析；同时，节点的拓扑势指标可以对节点重要度进行有效排序。

4 结论

在作战网络节点的重要度评估中，利用节点拓扑势指标可充分体现节点属性及其在网络结构上的相互作用；基于网络社团的改进最短路径距离算法，可准确求解出符合情报保障、指挥控制和作战协同关系约束的交互路径。在网络化作战体系中，体系网络的社团结构因受作战任务、资源的约束而复杂多变，社团的划分更加困难，为重要节点的评估发现、保护带来困难。下一步，笔者将研究复杂情况下的体系网络社团划分方式。

[1] Corley H, Sha D. Most Vital Links and Nodes in Weighted Network[J].Operations Research Letters, 1982, 1(4):157-160.

[2] Nardelli E, Proietti G, Widmayer P. Finding the Most Vital Node of a Shortest Path[J]. Theoretical Computer Science, 2001, 296(1):167-177.

[3] 刘建国, 任卓明, 郭强, 等. 复杂网络中节点重要性排序的研究进展[J]. 物理学报, 2013, 62(17):178901.

[4] 贾子英, 侯学隆, 潘大志. 网络化防空体系中作战单元重要度评估[J]. 现代防御技术, 2013,41(5): 12-16.

[5] 卞泓斐, 杨根源, 陈榕. 舰艇编队网络化防空体系中节点重要度评估[J]. 四川兵工学报, 2015, 36(8):15-19.

[6] 姜志鹏, 张多林, 马婧, 等. 基于加权网络模型的指挥节点重要度评估方法[J]. 装甲兵工程学院学报, 2014, 28(4):19-23.

[7] 蓝羽石, 毛少杰, 王衍. 指挥信息系统结构理论与优化方法[M]. 北京:国防工业出版社, 2015: 24-25.

[8] 金伟新, 肖田元. 作战体系复杂网络研究[J]. 复杂系统与复杂性科学, 2009, 6(4):12-25.

[9] 张健沛, 李泓波, 杨静, 等. 基于归属不确定性的变规模网络重叠社区识别[J]. 电子学报, 2012, 40(12):2512-2518.

[10] 李泓波. 基于拓扑势的网络社区发现方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2013.

[11] 段松青, 于兴隆, 吴斌, 等. 基于有向拓扑势的用户角色分析方法[J]. 通信学报, 2014, 35(12):124-134.

[12] 宋伟健,丁勇鹏,陈小卫.基于模糊偏序关系的装备保障点选址多属性决策[J]. 海军航空工程学院学报,2012,227 (1):103-106.

(责任编辑: 尚彩娟)

Node Importance Evaluation for Weighted Combat SoS Network

SUN Cheng-yu, SHEN Mao-xing, WANG Yu-feng, WANG Xin

(Air and Missile Defense College, Air Force Engineering University, Xi’an 710051, China)

For the issue of operational unit’s importance evaluation of combat SoS network, the weighted network model for combat SoS is established, and a new method based on topological potential is presented: firstly, multiple attribute decision making method based on fuzzy partial ordering relation is used to obtain the node attribution importance value; secondly, a new algorithm based on network community is designed to find the shortest distance between two nodes; finally, node topological potential which is obtained from the node attribution importance value and the shortest distance, is adopted as index of node importance. Experiments show that the designed shortest distance algorithm and the topological potential index are effective, which can be applied for the study of network invulnerability.

node importance; topological potential; multiple attribute decision making; weighted network

1672-1497(2016)05-0095-05

2016-08-08

孙成雨(1989-)，男，博士研究生。

E911; TP393.02

A

10.3969/j.issn.1672-1497.2016.05.020