基于加权峭度的滚动轴承故障特征提取
陈祥龙, 张兵志, 冯辅周, 江鹏程
(1. 装甲兵工程学院机械工程系, 北京 100072; 2. 北京特种车辆研究所, 北京 100072)
基于加权峭度的滚动轴承故障特征提取
陈祥龙1, 张兵志2, 冯辅周1, 江鹏程1
(1. 装甲兵工程学院机械工程系, 北京100072;2. 北京特种车辆研究所, 北京100072)
针对峭度谱(Kurtogram)无法有效区别振动信号中的瞬态故障冲击和脉冲噪声,难以准确提取微弱的滚动轴承故障特征的问题,提出一种基于加权峭度(WeightedKurtosis,WK)的滚动轴承故障特征提取方法,通过固定设置滤波带宽,利用加权峭度识别共振中心频率,确定带通滤波器的滤波中心频率和带宽,结合包络分析提取滚动轴承故障特征,并通过采集变速箱滚动轴承振动数据对该方法进行了验证。结果表明:该方法能够有效克服峭度谱的缺陷,稳健识别滚动轴承共振中心频率,准确提取滚动轴承故障特征,验证了该方法的有效性。
峭度谱; 加权峭度(WK); 滚动轴承; 特征提取
滚动轴承是机械设备最容易发生失效的部位之一,在机械设备状态监测和故障诊断时,需要及时有效地提取滚动轴承的故障特征,确保机械设备连续可靠运行,以避免因突发故障造成的不必要损失[1]。当滚动轴承发生局部故障时,轴承会以一定的故障通过频率产生具有共振频率调制特征的循环故障冲击,在振动信号中表现出频率调制特点。包络分析能够用于解调故障特征,但如何准确地识别滚动轴承共振频带是有效提取故障特征的关键[2]。
峭度(Kurtosis)能够有效检测信号中的瞬态故障冲击及其频带位置,识别包含瞬态故障冲击的共振频带。ANTONI等[3-5]最早提出利用峭度检测滚动轴承振动信号中的瞬态故障冲击成分,确定滚动轴承共振频带的频域位置;然后,基于二叉树频带划分带通滤波器组,提出了峭度谱(Kurtogram),以自适应确定共振频带并包络解调故障特征。LEI等[6]提出利用小波包变换替代二叉树划分频带,构造了一种改进峭度谱,用于滚动轴承故障诊断;WANG等[7]基于小波包变换和包络功率谱构造了一种增强峭度谱,能够增强滚动轴承故障特征提取效果;马新娜等[8]基于峭度识别共振中心频率,通过固定共振滤波带宽提出了一种典型峭度谱算法,有效地提取了滚动轴承故障特征。
但在实际工程应用中,受背景噪声和信号传递路径等因素的影响,滚动轴承故障特征比较微弱。同时,由于振动信号信噪比较低,噪声信号中的脉冲干扰也会引起滚动轴承振动信号瞬时能量的波动,导致峭度无法有效区分信号中的瞬态故障冲击与脉冲噪声,难以准确识别共振中心频率并提取滚动轴承故障特征。针对峭度的缺陷,研究者们提出了一些新的滚动轴承瞬态故障冲击检测方法,用于识别共振中心频率并包络解调滚动轴承故障特征:TSE等[9-10]提出了基于包络功率谱稀疏度的故障冲击检测方法;ANTONI等[11]提出了基于负熵的故障冲击检测方法;张龙等[12]提出了基于包络谱峰值因子的故障冲击检测方法;代士超等[13]提出了基于子频带平均峭度的故障冲击检测方法;樊新海等[14]提出了基于加权峭度(Weighted Kurtosis,WK)的故障冲击检测方法。
因此,在深入研究峭度以及峭度谱的基础上,笔者提出了一种基于加权峭度的滚动轴承故障特征提取方法,通过固定设置滤波带宽,利用加权峭度准确识别滚动轴承共振中心频率,结合包络分析提取滚动轴承故障特征,并通过采集变速箱滚动轴承振动数据验证了该方法的有效性。
1 基本原理
1.1峭度
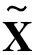
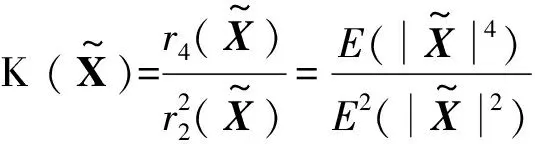
(1)
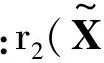
根据式(1),高斯分布实信号的峭度恒等于3,因此零均值实信号X的峭度也可表示为
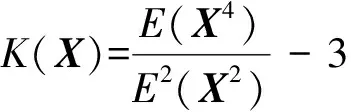
(2)
谱峭度(SpectralKurtosis,SK)是峭度在频谱上的构造形式,其基本思想是通过计算信号谱线上的峭度值,识别包含瞬态故障冲击特征的信号频段。谱峭度SK(f)可表示为
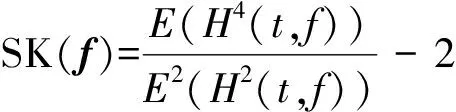
(3)
式中:H(t,f)为信号在频率f处的复包络。
1.2峭度谱
鉴于峭度在检测瞬态故障冲击中的优越性,ANTONI等[5]基于峭度提出了峭度谱的分层结构,如图1所示,其算法流程如下:
1) 设置峭度谱最大分析层数k,利用1/3二叉树均匀迭代划分信号滤波子频带,获得带通滤波器的滤波中心频率fc和带宽B′;
2) 依据带通滤波器滤波中心频率和带宽,构造带通滤波器组,获得子频带滤波信号;
4) 选取具有最大峭度值的带通滤波信号进行包络分析,提取故障特征。
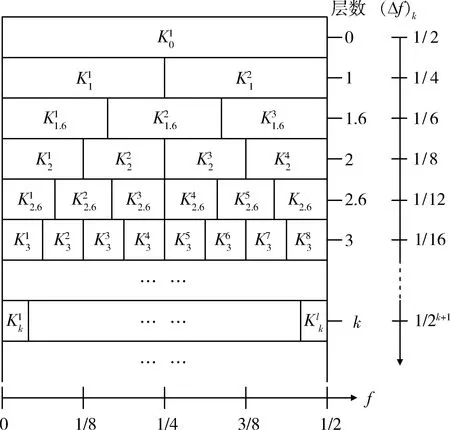
图1 峭度谱的分层结构
2 加权峭度及故障特征提取方法
2.1加权峭度
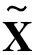
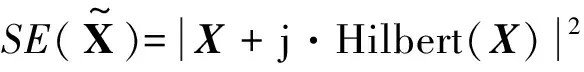
(4)
式中:SE(·)为平方包络信号;Hilbert(·)为希尔伯特解析运算;j为虚数。
根据文献[11]、[14]中的推导计算,将式(4)代入式(1),则可将式(1)改写为

(5)
式中:d[·]表示标准差。
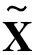
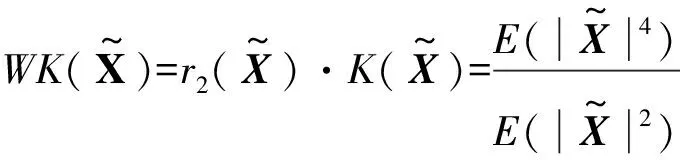
(6)
2.2基于加权峭度的故障特征提取方法
在结合峭度谱和加权峭度的基础上,笔者提出了基于加权峭度的滚动轴承故障特征提取方法,其算法流程如图2所示。
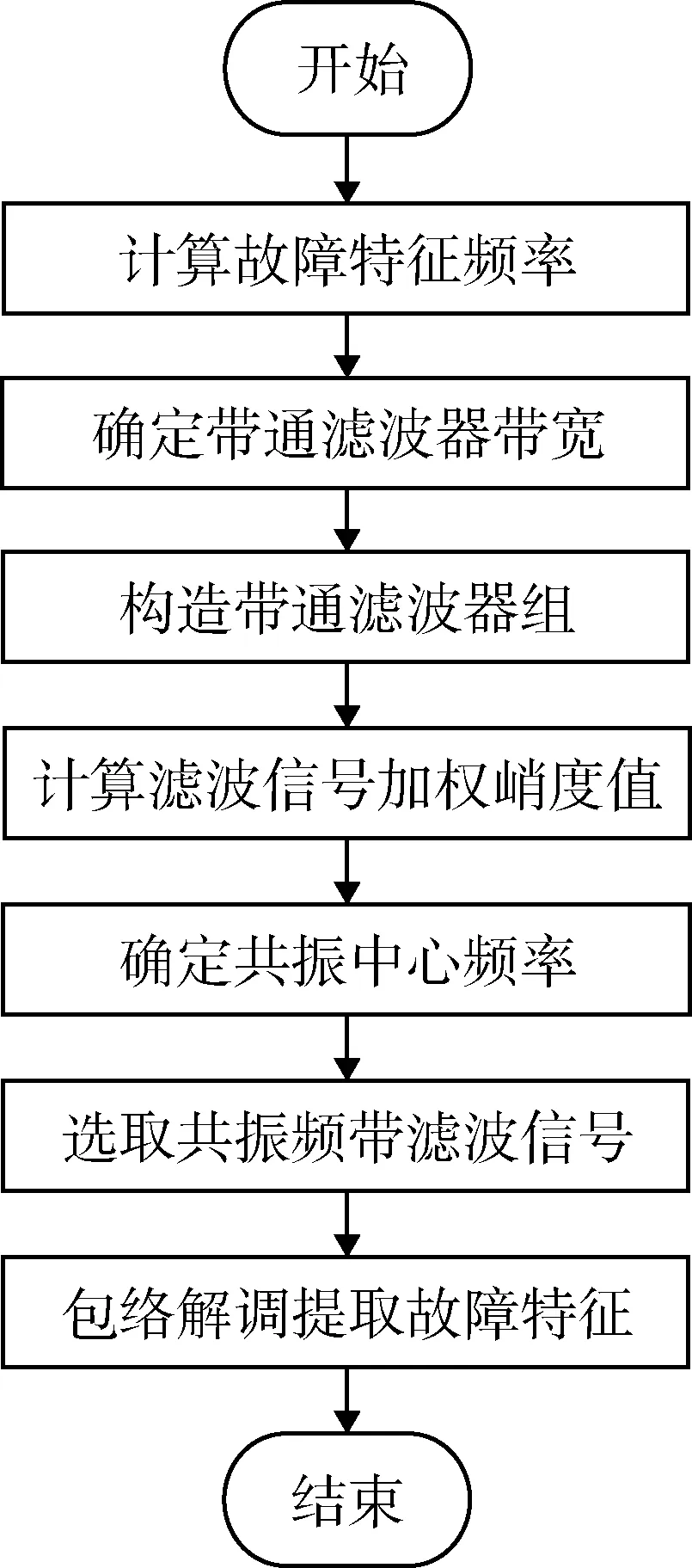
图2 基于加权峭度的滚动轴承故障特征提取方法的算法流程图
基于加权峭度的滚动轴承故障特征提取方法的算法流程描述如下:
1)根据滚动轴承几何参数和机械系统运行工况,计算滚动轴承的故障特征频率ffault。
2)根据文献[8],在滚动轴承故障特征提取中,带通滤波器带宽应不小于3倍的滚动轴承故障特征频率,即B′≥3ffault。
3)以fs为采样频率,在[0.5B′,fs-0.5B′]频率范围内,以0.5B′为初始带通滤波器中心频率,以B′为带通滤波器带宽,以0.2ffault为滤波器滤波中心频率的步长,构造带通滤波器组。
4)利用带通滤波器组对滚动轴承信号进行滤波,计算各滤波信号频谱的加权峭度,标记具有最大加权峭度值的滤波信号所对应的中心频率为共振中心频率fc。
5) 选取共振频带[fc,B′]的滤波信号并进行包络分析,提取滚动轴承故障特征。
3 仿真分析
利用滚动轴承数值仿真模型模拟滚动轴承外圈故障,验证基于加权峭度的滚动轴承故障特征提取方法的有效性。数值仿真模型表示为[2]
(7)
设置滚动轴承的故障特征频率ffault=100 Hz,T=1/ffault=0.01 s,A=1,B=3,C=900,D=600,fm=2 500 Hz,fn=4 000 Hz,t1=0.125 s,t2=0.225 s,仿真信号信噪比SNR=-12.8 dB,采样频率fs=12.8 kHz,采样点数为6 400,其滚动轴承仿真信号时域波形、频谱以及平方包络谱如图3所示。由图3可以看出:受强背景噪声影响,表征故障特征的瞬态冲击淹没于噪声信号中,导致仿真信号的信噪比较低,仿真信号的频谱和平方包络谱中均难以识别出有价值的故障特征信息。
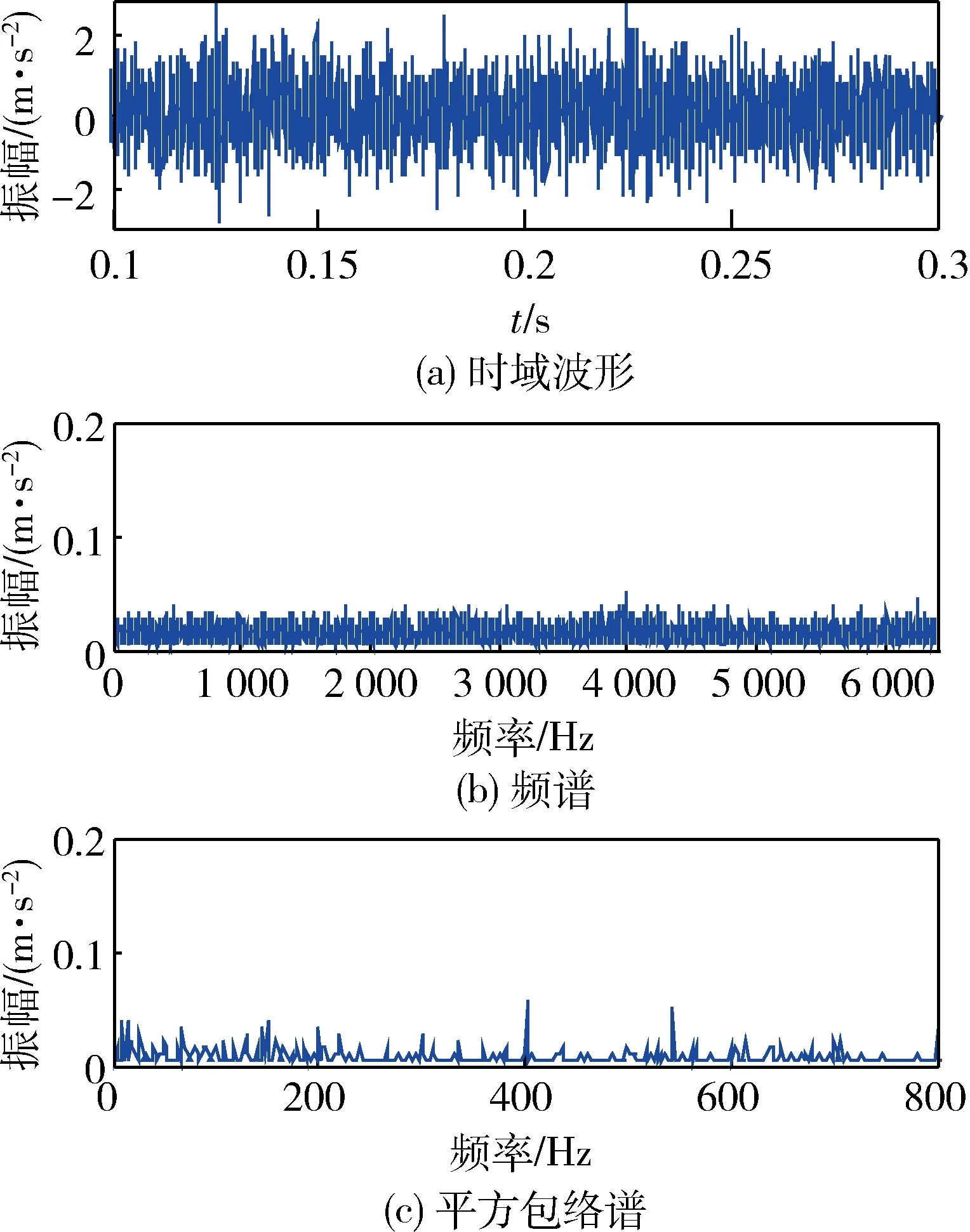
图3 滚动轴承仿真信号
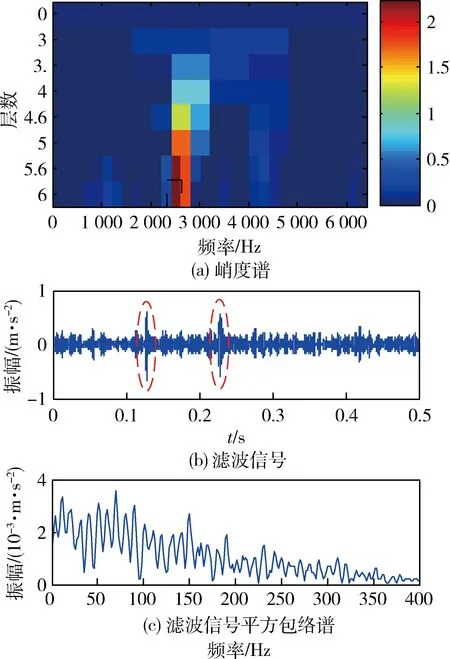
图4 基于峭度谱的滚动轴承仿真信号分析结果
利用峭度谱算法提取滚动轴承仿真信号的故障特征,其基于峭度谱的滚动轴承仿真信号分析结果如图4所示。由图4(a)可以看出:具有最大峭度的滤波信号在第6层,对应共振中心频率为fc=2 400 Hz,带宽B′=400Hz,说明峭度谱识别的共振中心频率与脉冲噪声的共振中心频率fm=2500Hz基本吻合。由图4(b)可以看出:滤波信号中清晰地包含脉冲噪声成分。由图4(c)可以看出:受强背景噪声以及噪声脉冲干扰等因素的影响,导致平方包络谱中无法提取出滚动轴承故障特征。
利用基于加权峭度的滚动轴承故障特征提取方法分析同一组信号,在150~6 250 Hz频率范围内,设置初始带通滤波器滤波中心频率为150 Hz,带宽为300 Hz,步长为20 Hz,构造带通滤波器组。其基于加权峭度的滚动轴承仿真信号分析结果如图5所示。
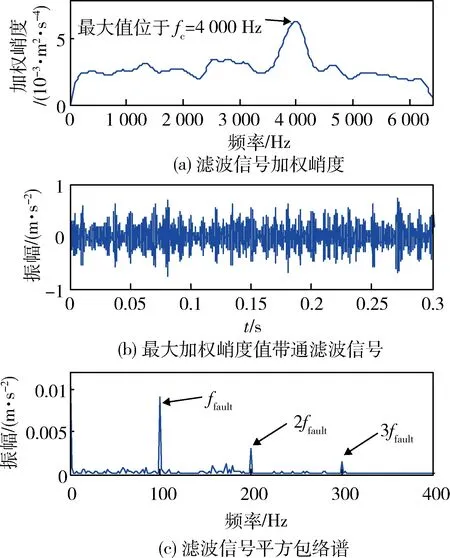
图5 基于加权峭度的滚动轴承仿真信号分析结果
由图5(a)可以看出:具有最大加权峭度值的滚动轴承滤波信号对应共振中心频率fc=4 000 Hz,与模拟轴承共振频率相一致。由图5(b)可以较清晰地看出故障冲击信号。由图5(c)可以看出:平方包络谱中能够清晰地提取出信号的故障特征频率及其倍频。
由图5可以得出:基于加权峭度的滚动轴承故障特征提取方法能够克服强背景噪声以及脉冲噪声干扰等因素的影响,准确识别出仿真信号中包含瞬态故障冲击共振中心频率,提取出故障特征频率及其倍频。
4 试验验证
为进一步验证基于加权峭度的滚动轴承的故障特征提取方法的有效性,对某型变速箱滚动轴承振动数据进行采集,其变速箱试验装置组成如图6所示。该变速箱输出轴支撑轴承为深沟球轴承,振动传感器安装在其对应的机体位置。采用电火花加工法在堪用轴承的外圈设置尺寸微小的点状缺陷,模拟轴承外圈点蚀剥落故障,采集滚动轴承振动信号和输出轴转速信号。设置采样频率为12 kHz,试验时的输出轴转频为fr=29.5 Hz,滚动轴承外圈故障特征频率为106 Hz。
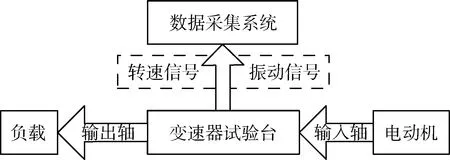
图6 某型变速箱试验装置组成
一组滚动轴承外圈故障振动信号的时域波形、频谱及其平方包络谱如图7所示。可以看出:该信号的频谱及其平方包络谱中很难直接提取出任何故障特征信息。
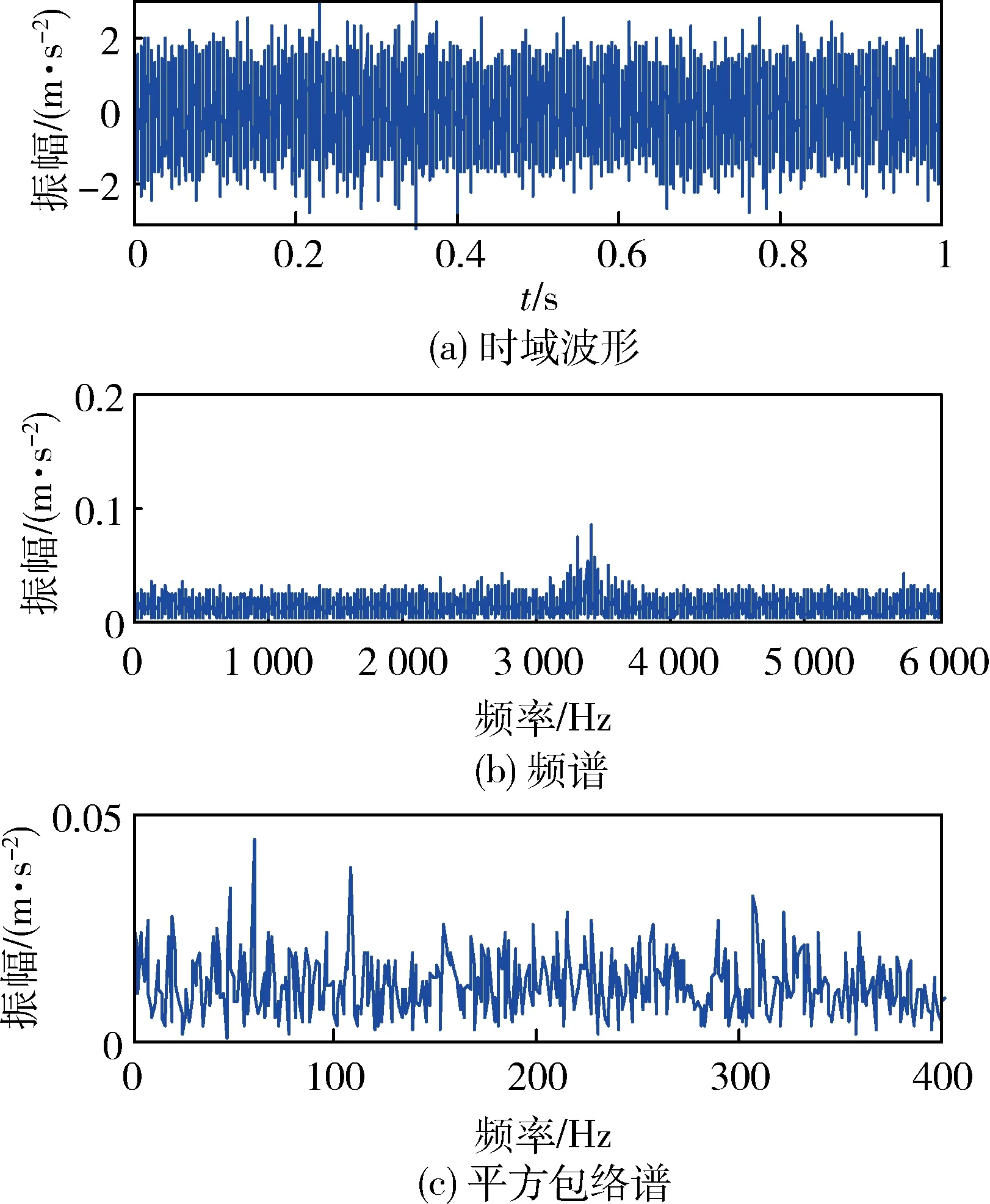
图7 一组滚动轴承外圈故障振动信号
利用峭度谱算法分析该组滚动轴承外圈故障振动信号,基于峭度谱的分析结果如图8所示。由图8(a)可以看出:具有最大峭度值的滤波信号位于谱图的第5.6层,对应共振中心频率为fc=4 687 Hz。由图8(b)可以看出:滤波信号中无法识别出循环发生的瞬态故障冲击,却包含有异常的噪声脉冲。由图8(c)可以看出:平方包络谱中无法清晰地识别出滚动轴承外圈故障特征频率。
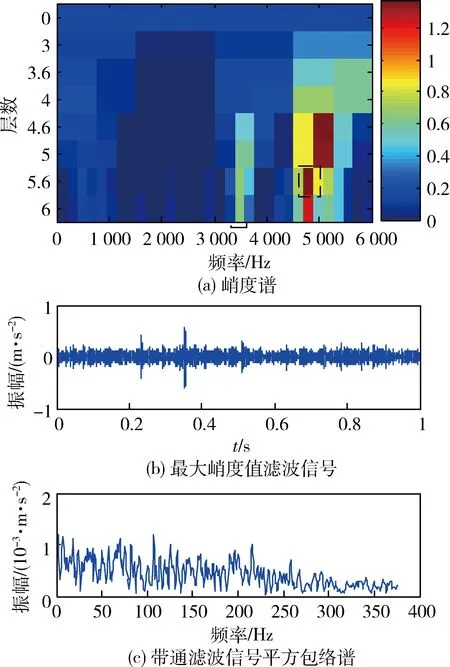
图8 基于峭度谱的滚动轴承外圈故障振动信号分析结果
利用基于加权峭度的滚动轴承故障特征提取方法分析该组滚动轴承外圈故障振动信号,基于加权峭度的分析结果如图9所示。由图9(a)可以看出:具有最大加权峭度值的滤波信号对应共振中心频率fc=3 450 Hz。由图9(b)可以较清晰地识别出循环瞬态冲击。由图9(c)可以看出:基于加权峭度的滚动轴承故障特征提取方法能够清晰地提取出滚动轴承外圈故障振动信号的转频、故障特征频率及其倍频,验证了该方法的有效性。
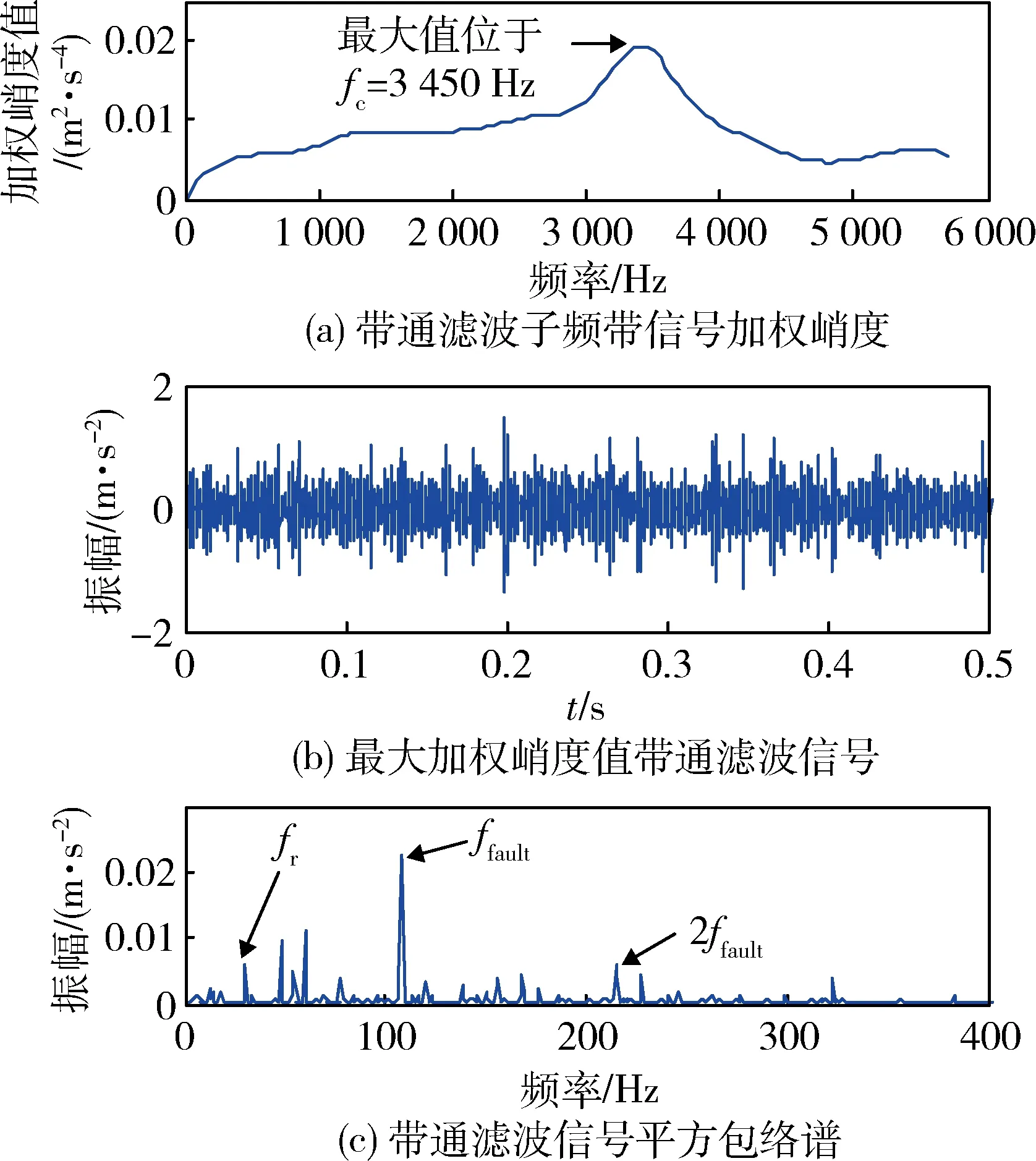
图9 基于加权峭度的滚动轴承外圈故障振动信号分析结果
5 结论
基于加权峭度的滚动轴承故障特征提取,通过固定设置滤波频带带宽,利用加权峭度检测瞬态故障冲击,能够克服峭度谱的不足,稳健识别滚动轴承共振中心频率,准确提取出滚动轴承故障特征。仿真和试验分析结果验证了该方法的有效性。
[1] SMITH W A,Randall R B.Rolling element bearing diagnostics using the Case Western Reserve University data:a benchmark study[J].Mechanical systems and signal processing,2015(64/65):100-131.
[2] CHEN X,FENG F,ZHANG B.Weak fault feature extraction of rolling bearings based on an improved Kurtogram[J].Sensors,2016,16(9):1482.
[3] ANTONI J.The Spectral Kurtosis:a useful tool for characterising non-stationary signals[J].Mechanical systems and signal processing,2006,20(2):282-307.
[4] ANTONI J,RANDALL R B.The Spectral Kurtosis:application to the vibratory surveillance and diagnostics of rotating machines[J].Mechanical systems and signal processing,2006,20(2):308-331.
[5] ANTONI J.Fast computation of the Kurtogram for the detection of transient faults[J].Mechanical systems and signal processing,2007,21(1):108-124.
[6] LEI Y,LIN J,HE Z,et al.Application of an improved Kurtogram method for fault diagnosis of rolling element bearings[J].Mechanical systems and signal processing,2011,25(5):1738-1749.
[7] WANG D,TSE P W,TSUI K L.An enhanced Kurtogram method for fault diagnosis of rolling element bearings[J].Mechanical systems and signal processing,2013,35(1/2):176-199.
[8] 马新娜,杨绍普.典型快速谱峭图算法的研究及应用[J].振动与冲击,2016,35(15):109-114.
[9] TSE P W,WANG D.The automatic selection of an optimal wavelet filter and its enhancement by the new sparsogram for bearing fault detection[J].Mechanical systems and signal processing,2013,40(2):520-544.
[10] TSE P W,WANG D.The design of a new sparsogram for fast bearing fault diagnosis:Part 1 of the two related manuscripts that have a joint title as “Two automatic vibration-based fault diagnostic methods using the novel sparsity measurement-Parts 1 and 2”[J].Mechanical systems and signal processing,2013,40(2):499-519.
[11] ANTONI J.The infogram:Entropic evidence of the signature of repetitive transients[J].Mechanical systems and signal processing,2016,74:73-94.
[12] 张龙,熊国良,黄文艺.复小波共振解调频带优化方法和新指标[J].机械工程学报,2015,51(3):129-138.
[13] 代士超,郭瑜,伍星,等.基于子频带谱峭度平均的快速谱峭度图算法改进[J].振动与冲击,2015,34(7):98-102.
[14] 樊新海,张传清,刘相波,等.基于短时加权峭度的信号冲击特征提取[J].装甲兵工程学院学报,2016,30(5):73-76.
[15] BORGHESANI P,PENNACCHI P,CHATTERTON S.The relationship between kurtosis-and envelope-based indexes for the diagnostic of rolling element bearings[J].Mechanical systems and signal processing,2014,43(1/2):25-43.
(责任编辑: 尚菲菲)
ExtractingFaultFeaturesofRollingBearingsBasedonWeightedKurtosis
CHEN Xiang-long1, ZHANG Bing-zhi2, FENG Fu-zhou1, JIANG Peng-cheng1
(1. Department of Mechanical Engineering, Academy of Armored Force Engineering, Beijing100072, China;2. Beijing Special Vehicle Research Institute, Beijing100072, China)
As the Kurtogram cannot effectively differentiate noise impulse and transient fault shock in the vibration signal, it is difficult to extract weak fault features of rolling bearings, a novel method based on Weighted Kurtosis(WK) is proposed to extract fault features of rolling bearings in this paper. The proposed method utilizes a WK to identify the resonant central frequency and confirm the band-pass filter central frequency by setting triple fault frequency as filtered bandwidth, coupling with envelope analysis. Finally, rolling bearing vibration data sampled from gearbox are ultilized to verify the efficiency of the proposed method. The results show that, the proposed method can effectively overcome the defects of Kurtogram, steadily identify resonant central frequency band, and accurately extract fault features of rolling bearings. The validity of the method is verified.
Kurtogram; Weighted Kurtosis (WK); rolling bearing; feature extraction
1672-1497(2017)04-0046-06
2017-03-04
军队科研计划项目
陈祥龙(1989-),男,博士研究生。
TH133.3;TP206
:ADOI:10.3969/j.issn.1672-1497.2017.04.009

