基于动态阈值函数的改进小波包遥测信号去噪方法

胡 健，玄志武，刘 学，徐洪洲

(中国人民解放军91550部队，辽宁 大连 116023 )

0 引言

在进行飞行器试验时，通过利用遥测信号来获取飞行器的工作状态和环境数据，为评定性能和故障分析提供依据。因此，遥测信号的好坏影响到对飞行器性能的判断和改进，以及飞行故障的原因分析和部位定位。由于遥测信号在试验中易受到环境噪声和测量噪声的干扰，所以在进行遥测数据处理前，对遥测信号进行去噪预处理是必不可少的重要步骤。

早期采用傅里叶变换法[1-3]来去除遥测信号噪声，在处理有效信号和噪声信号重叠较多的情形时效果不太理想，具有局限性。小波变换[4-6]因具有较好的时频局部化特性，特别适用于非平稳信号分析，近年来在遥测信号去噪领域得到了广泛应用。但是小波去噪法不对高频细节信号进行分解，较难刻画信号的局部边缘特性。因此虽然小波分析方法比传统的傅立叶方法消除噪声干扰效果好，但有时并不是十分理想。小波包去噪法[7-9]是在小波去噪法的基础上，对信号分解后的各个频段同时进行分析。小波包分析与小波分析相比，由于同时对上一级分解信号的低频和高频部分进行分解，能够进一步去除高频信号中的噪声，提高了频率分辨率，对于细节信号刻画更加精细。

小波包去噪的关键是阈值的选取及阈值函数的定义，为提高小波包去噪法的效果，针对阈值选取开展了大量研究。目前较为常见的小波包去噪法阈值准则有4种：固定形式阈值准则(Sqtwolog)、自适应阈值准则(Rigrsure)、启发式阈值准则(Heursure)、极小化极大阈值准则(Minimaxi)。其中，去噪效果最好的是Sqtwolog准则，但是也最易造成有用信号的丢失，适合高频段使用。最保守的是Minimaxi准则，但能够保证有效信号不易丢失，适合低频段使用。因此，文献[10-11]采用了多阈值准则的小波包去噪方法，对小波包分解的高频系数和低频系数采用不同的阈值准则处理，提高了去噪效果。对于阈值函数的定义，目前普遍使用的是阈值函数，它是由Donoho提出的硬阈值函数和软阈值函数。其中，硬阈值函数可以较好地保留信号边缘等局部特性，但是由于不连续，使得重构信号出现原有信号没有的振荡，所以适合突变信号。软阈值函数处理信号时具有较好的连续性，处理效果相对平滑，但去噪后信号幅值会出现与原信号偏差的情形，适合处理平滑信号。针对软、硬阈值函数的研究，文献[12]通过控制噪声和信号之间的过渡区域的衰减程度，更加符合自然信号的连续性；文献[13]提出一种基于Shannon熵的自适应小波包阈值去噪算法，实现在不同噪声强度背景下，阈值函数的平滑过渡。这些通过改进阈值函数的方法，扩大了小波包去噪方法的适用范围。

本文在传统小波包去噪方法的基础上，提出一种基于动态阈值函数的改进小波包遥测信号去噪方法：1)首先根据小波包分解后的不同频段，根据各分频段的特征，采用不同的阈值准则，来代替单一阈值准则;2)其次对阈值函数进行改进，构建一个介于硬阈值函数和软阈值函数之间并可切换的动态阈值函数，通过在阈值函数中量化待分解信号的平滑程度，来改变新阈值函数的软硬程度。在处理信号平滑部分时，动态阈值函数向软阈值函数转变，在处理信号突变部分时，动态阈值函数向硬阈值函数转变。最后，利用本文所提方法与传统小波包方法对仿真算例信号进行去噪比较，结果表明本文方法对信号去噪后，能在保持良好信号边缘特性的同时，有效减小振荡，具有更好的去噪效果。

1 小波包去噪理论

小波变换主要适用对信号的低频部分进行分解，较难对高频部分进行分解，因此去噪效果不够精细。而小波包信号可以没有遗漏地对信号全频进行分解，因此不会丢失信号高频部分的有用信息。其信号分解的过程是利用高-低通共轭滤波器将信号进行分解，这过程中会引起各层分解信号的频率顺序与节点的顺序不一致。以3层小波包分解为例，其分解结构如图1所示。

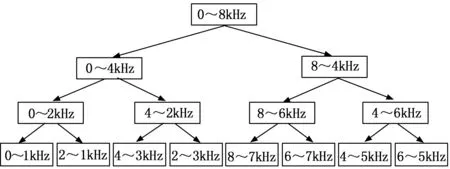
图1 3层小波包分解结构图

小波包去噪的步骤如下：

1)选取合适的小波包分解层次，利用小波包分解公式，对信号进行小波包分解；

其中，小波包的分解公式如式(1)：

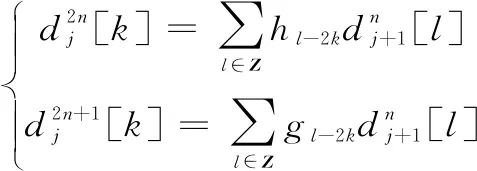
(1)

式中，dj2n和dj2n+1分别表示第j层第2n个节点和第j层第2n+1个节点的小波包系数。h和g为滤波器系数。

2)选取最优小波包基，确定最优树：小波包基是一组小波包的正交规范基，因此对于需要去噪的信号，小波包基可以有很多个。在进行小波包去噪时，根据不同的小波包基的时频特性进行选取，最终的去噪效果也会不同。为了达到最好的去噪效果，在用小波法去噪时，会采用选取最优小波包基来提高去噪效果。选取最优小波包基方法是，通过一个熵标准，利用代价函数取最小值时来确定最优小波包基。

3)进行阈值计算和阈值函数处理：通过阈值法来确定小波包系数，使得有效信号分量对应的小波包系数较大，而噪声信号分量对应的小波包系数较小。然后通过与阈值的比较，只保留大于阈值的小波包系数，而比阈值小的小波包系数则被舍去忽略不计，这样就把噪声信号分量给消去了。阈值法适合用于信噪比较大的信号消噪处理，其中阈值的选择是关键，若阈值取得过于保守，在消噪的过程中可能会损失部分有用信号，若阈值选择过小，则去噪效果不理想。

4)根据小波包重构公式，通过利用阈值处理后的小波包系数进行小波包重构。

小波包重构公式如式(2)：

(2)

2 改进的小波包去噪方法

由于飞行器在飞行试验过程中，通常存在飞行状态的改变，改变过程中测量参数往往会在平缓变化下突然发生较大改变，飞行器遥测信号是既包含平滑成分也含突变成分，因此在去噪的过程中，不能简单地认为低频段反映的是有用信息，高频段的是噪声。此时若使用传统阈值函数法进行去噪处理，不能在保持良好信号边缘特性与消除恒定偏差的同时，又能避免出现信号原本没有的振荡。

本文针对遥测信号复杂成分，提出一种基于动态阈值函数的改进小波包遥测信号去噪方法，主要分为阈值准则的选取，和对阈值函数进行改进，引入平滑因子根据信号实时改变阈值函数软硬程度，步骤如下所述。

2.1 阈值准则选取

目前4种常用的阈值准则表达式如下所示：

1)固定形式阈值准则(Sqtwolog)。其表达式形式固定，如式(3)所示：

(3)

式中，N为信号的长度，σ为信号噪声标准差。

2)自适应阈值准则(Rigrsure)。其表达式如式(4)所示：

(4)

式中，Q为根据无偏似然估计得到的分解系数平方。

3)启发式阈值准则(Heursure)。其表达式如式(5)所示：

(5)

式中，W为长度为N的信号小波包分解系数平方和。

4)极小化极大阈值准则(Minimaxi)。其表达如式(6)所示：

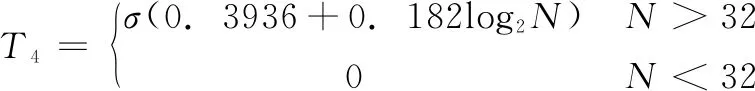
(6)

由于4种阈值准则根据频率分布均有自己的适用范围，因此只选用一种阈值准则对小波包分解系数进行处理有可能造成过度去噪或者去噪效果不理想。本文采用文献[11]所提的分段阈值准则，根据频段选用合适的准则，其选取如表1所示。

表1 分段阈值准则

2.2 改进的动态阈值函数

目前广泛使用的传统阈值函数是Donoho提出的软硬阈值函数，其表达式如式(7)和式(8)所示：

(7)

(8)

传统的硬阈值和软阈值函数都存在各自的缺点：对于硬阈值函数，当小波包原始分解系数小于阈值时，将其清为零，大于时则保持不变，这种处理方式适合处理突变信号，但这种不连续的处理方式，在处理平滑信号时，容易错误的重构出系统原本没有的振荡。对于软阈值函数，当小波包原始分解系数小于阈值时，将其清为零，大于阈值时则将原始小波包系数的绝对值与阈值的差作为处理后的小波包分解系数，这种处理方式适合平滑信号，但这使得去噪后信号幅值存在恒定差值，丧失高频特征，影响重构精度。

为了改进传统阈值函数法的不足之处，本文提出了一种新的动态阈值函数，首先用参数R来量化信号平滑程度，其表达式如下：

(7)

式中，N为信号长度，Rn为第n个信号点的平滑程度的量化值，其取值在0～1之间，当R为0的时候表示信号值在此刻值与前一刻值不变，值越大表示信号突变程度越大。提出改进的阈值函数表达式如式(8)所示：

(8)

根据式(8)可知，

(9)

(10)

再对所提阈值函数进行分段分析：

(1)当|d|≥λ时：

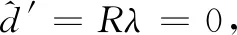
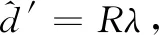
(2)当Rλ≤|d|<λ时：

当R值为最大值1时，Rλ=λ，式(8)等号右边第二式可以和第一式合并，变为硬阈值函数；

当R值为最小值0时，Rλ=0，式(8)等号右边第二式可以和第三式合并，变为软阈值函数；

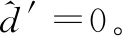
3 实验结果与分析

采用仿真信号和试验算例对本文所提的基于动态阈值函数的改进小波包去噪方法，同传统小波包硬阈值函数法、软阈值函数法进行性能对比验证，选择信噪比(SNR)和均方根误差(RMSE)来对比各方法的去噪效果。

(11)

(12)

3.1 仿真信号分析

构造仿真信号如式(13)所示：

ψ(τi,θi)=

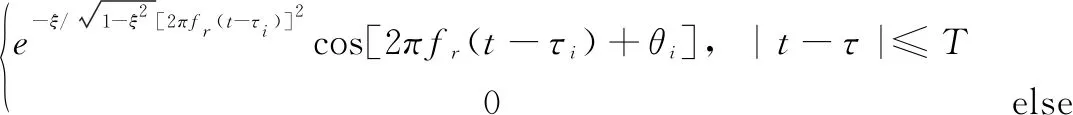
(13)

其中：n(t)为高斯白噪声，信号长度N=1 024，采样频率为fs=10 kHz，A=[4.5,6,4]和θ=[π/6,π/4,π/3]和分别为给定的幅值和初始相位向量，驱动频率fr=1 kHz，阻尼系数ξ=0.01，τ=[0.02,0.06,0.1]为脉冲起始时刻，T为脉冲持续时间，n(t)为加入-2 dB的高斯白噪声。

通过对比db系列小波包基函数输出信噪比后，采用db4小波包基函数进行5层小波包分解，表2为去噪效果对比，图2为原始信号，图3为含噪信号图，图4～6分别为传统小波包软阈值函数法、硬阈值函数法、以及本文方法的去噪效果。

图2 原始信号

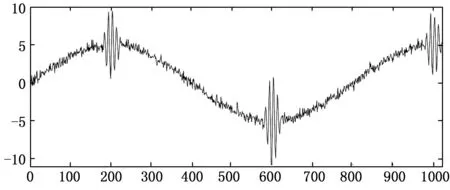
图3 含噪信号

图4 软阈值法去噪效果

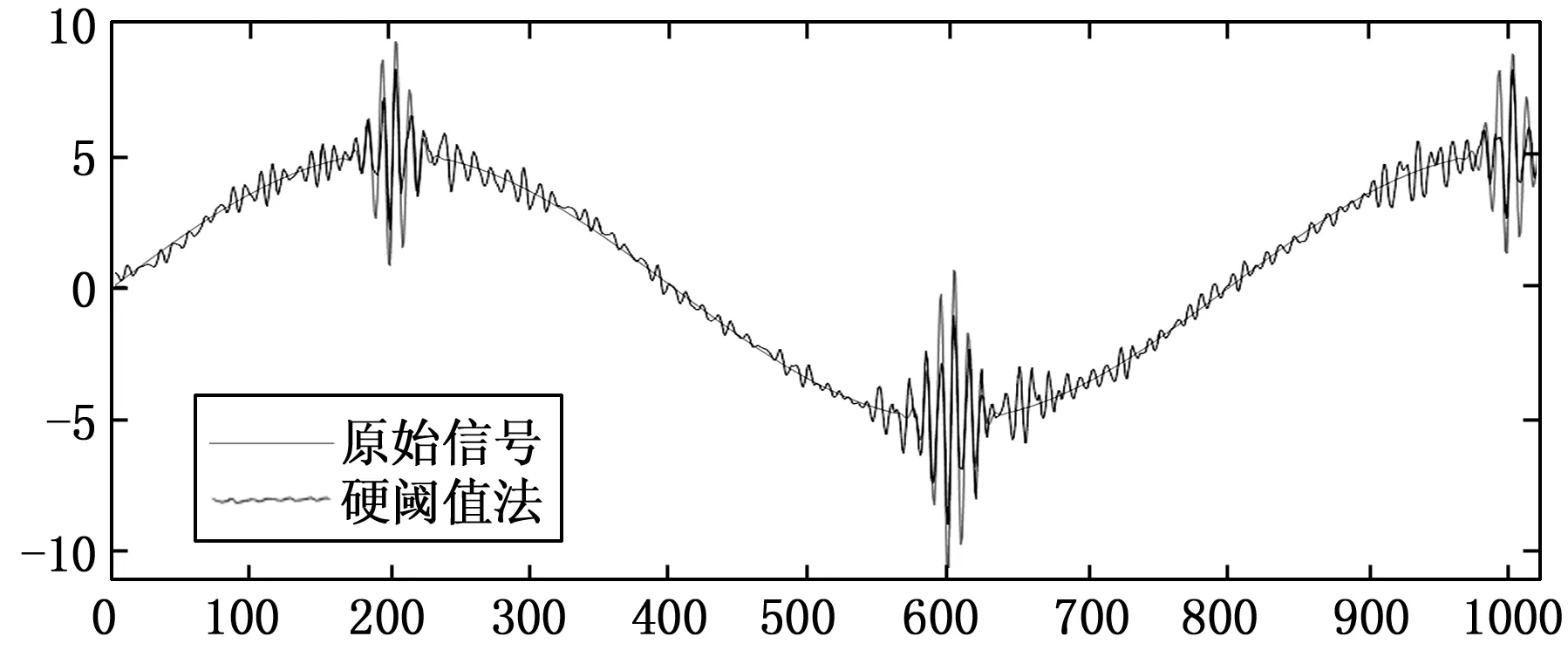
图5 硬阈值法去噪效果

图6 本文方法去噪效果

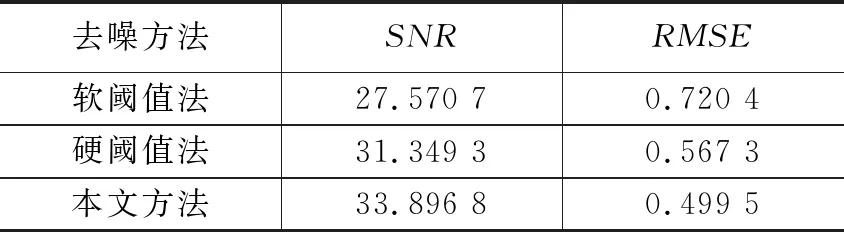
去噪方法SNRRMSE软阈值法27.570 70.720 4硬阈值法31.349 30.567 3本文方法33.896 80.499 5

由图4可以看出，用传统小波包软阈值去噪方法进行去噪时，虽然原始信号平滑部分获得了较好的去噪效果，但是遇到信号突变时，丢失了原始信号的高频特征；由图5可以看出，用传统小波包硬阈值去噪方法进行去噪时，由于阈值函数的不连续性，在信号发生突变前后，重构信号出现了原始信号和含噪信号都没有的振荡；由图6可以看出，用所提方法进行去噪时，高频特征得到了保留的同时，在信号突变前后，并未在增加原始信号没有的振荡信号，对噪声信号起到了较好的去噪作用。

由表2对比可以看出，本文所提方法提高了信噪比，降低了均方根误差证明了本文方法的有效性。

3.2 试验信号分析

选取飞行器试验过程中某压力遥测信号进行分析。通过对比db系列小波包基函数输出信噪比后，采用db4小波包基函数进行6层小波包分解，图7～9分别为传统小波包软阈值函数法、硬阈值函数法、以及本文方法的去噪效果示意图。

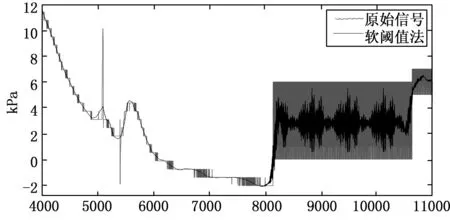
图7 软阈值法去噪效果

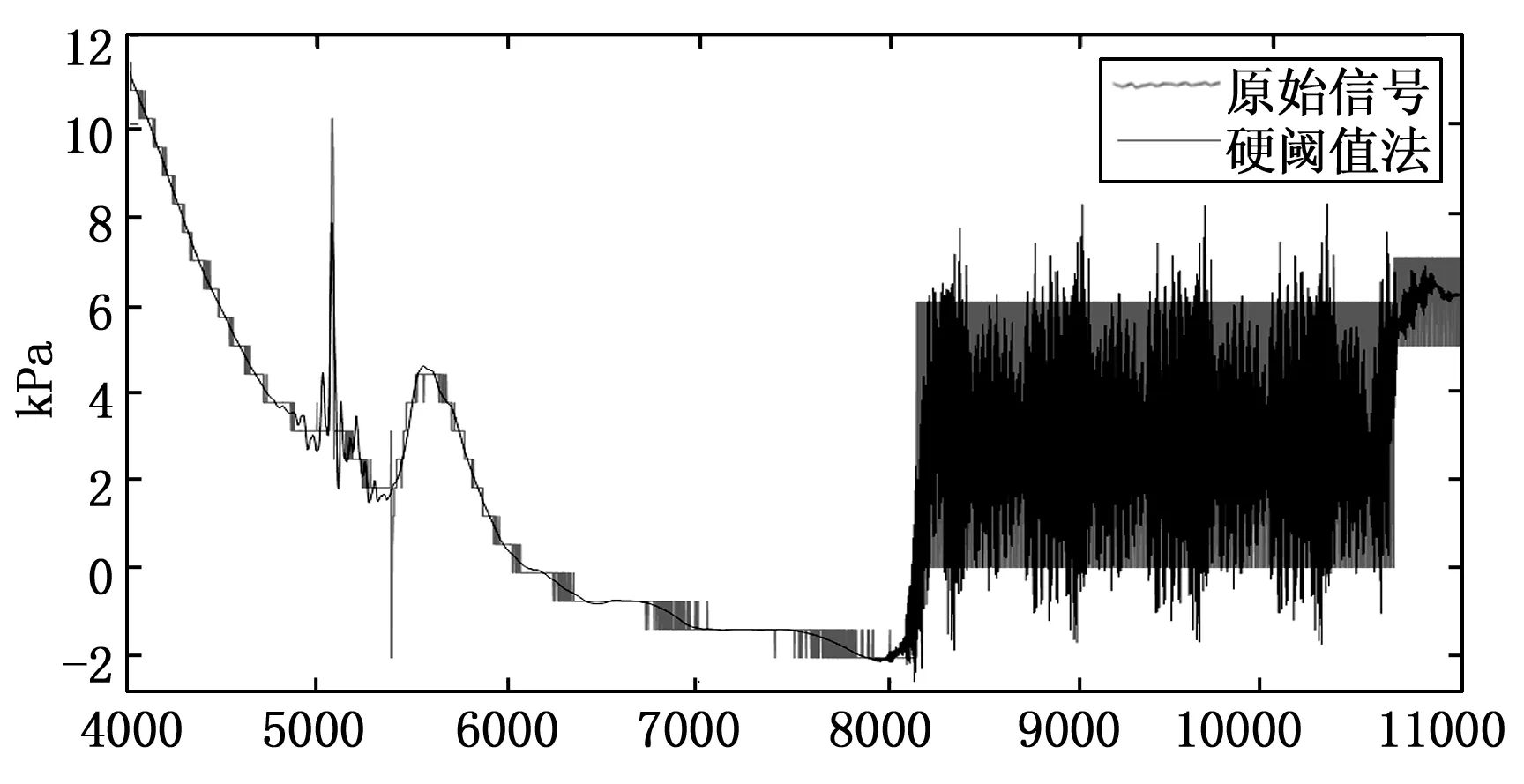
图8 硬阈值法去噪效果

由图7可以看出，用传统小波包软阈值去噪方法对遥测信号进行去噪时，信号平滑段发生突变后，高频特征存在丢失；由图8可以看出，用传统小波包硬阈值去噪方法进行去噪时，由于阈值函数的不连续性，对于信号发生变化较多的部分，重构信号虽然高频特征得到恢复，但是振荡变得更剧烈了；由图9可以看出，用所提方法进行去噪时，高频特征得到了保留的同时，在信号突变前后，并未在增加原始信号没有的振荡信号，对噪声信号起到了较好的去噪作用。

图9 本文所提方法去噪效果

通过算例对比，证明本文方法在处理既含突变又含平滑信号时，比传统小波包法具有更好的去噪效果。

4 结束语

针对传统小波包去噪方法的阈值函数在处理既含突变又含平滑信号的情形下，不能在保持良好信号边缘特性与消除恒定偏差的同时，又能避免出现信号原本没有的振荡的问题，本文通过采用改进阈值函数的方法，利用量化反映信号的平滑程度的信息来对阈值函数进行调整，使得去噪方法在处理既含平滑又含突变信号时，能够分别采用适合各信号特征的阈值函数进行处理，避免了去噪后出现信号原本没有的振荡的同时，有效保留信号的高频特征，提高重构精度。