导弹武器射程评估的多因素正交试验设计方法
胡庆军, 王炯琦
(国防科学技术大学理学院数学与系统科学系,湖南长沙410073)
导弹武器射程评估的多因素正交试验设计方法
胡庆军, 王炯琦
(国防科学技术大学理学院数学与系统科学系,湖南长沙410073)
[摘要]“问题驱动”式的教学理念、教学模式和方法是教学改革和发展的趋势.以导弹武器射程鉴定与评估为背景,探讨了正交试验设计的课程教学在其中的应用.通过对影响导弹武器射程因素的分析,在确定的水平条件下,进行正交试验设计,得到较好的组合方式.从理论分析和仿真案例,回答了多因素水平下的导弹射程试验评估问题.通过“问题驱动”,不仅有利于提高学生学习兴趣和积极性,同时还有利于加深对理论和方法的认识和理解.
[关键词]问题驱动; 试验设计; 多因素; 武器射程
1引言
在第二次世界大战后期(1942年)德国研制成了V-2火箭.后来,一些国家以V-2为基础,逐步进行改进,到目前为止,已经出现了射程不同、性能不同、用途不同的各种导弹.
导弹是一种携带战斗部,依靠自身动力装置推进,由制导系统导引控制飞行航迹,导向目标并摧毁目标的飞行器.其组成包括战斗部、控制系统、发动机装置、弹体.导弹既可以携带普通弹头,用于常规的实战,也可以携带核弹头,用于战略威慑.它早已成为现代战争中最重要的武器之一.
作为导弹技战术的一个重要指标,导弹射程直接决定着导弹的打击效能.然而,在导弹研发过程中,影响导弹射程的因素往往很多,包括推进器、助推器、燃料、射向、射角、导弹载荷、空间环境、抗干扰能力以及操作人员的水平等,而每一因素的改变都有可能影响导弹武器的射程,当然有些因素影响较大,有些因素影响较小.目前,在我国各靶场进行的导弹武器试验鉴定,就是要找出哪些是主要影响因素,哪些是次要影响因素,以便在后续的导弹研发和生成过程中加以改进.
导弹武器的试验与鉴定,就是通过一系列实弹试验,获取足够有价值的数据资料(信息),并将所获得的数据进行处理、逻辑组合和综合分析,将其结果与装备研制总要求中规定的战术技术指标(射程、精度、毁伤效果)和作战使用要求进行分析比较,对实现导弹武器研制目标的情况进行评价,对导弹武器装备(包括系统、分系统及其部件)的战术技术性能和作战使用性能进行评定的过程.其目的是为装备定型、部队使用、研制单位验证设计和检验生产工艺提供科学决策依据.
然而,从导弹靶场试验鉴定角度来看,导弹试验具有小子样试验特点,也就是说由于实弹射击是消耗性的,不可能进行大量试验,因而从统计意义上看,属小子样范围.针对导弹试验小子样的特点,相对于试验数据分析而言,试验设计更为重要,如何设计好的试验方案,从而使得通过尽少的试验次数,来得到反映整体能力的试验结果.这就是试验设计所要解决的问题.
本文以导弹武器射程的评估为研究背景,利用正交试验设计方法,进行了导弹武器射程评估的多因素正交试验设计研究,给出了正交试验设计表格的设计方案,并利用极差分析法对试验数据进行合理性分析.
2问题描述及正交试验方案
2.1 问题描述
问题某基地进行导弹武器射程的鉴定与评估,通过靶场实弹测试,要寻找影响武器系统射程的主要因素.为简单起见,先考虑如下四个因素,分别是推进器(A)、燃料(B)、射向(C)、空间环境(D),并假定以上因素间无交互作用,由此确定了各因素的三个不同水平如下表1所示.
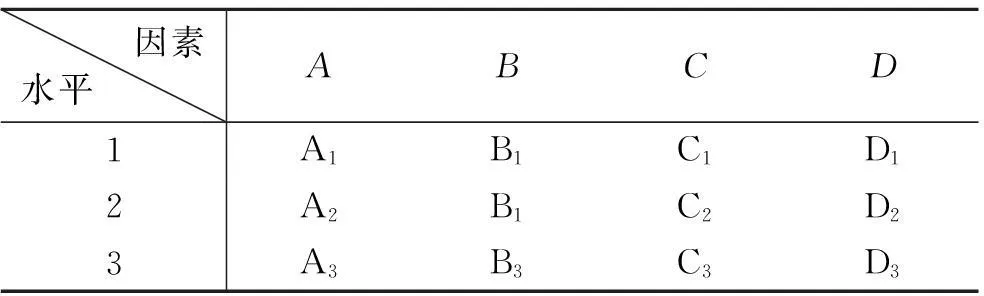
表1 导弹武器射程试验影响因素及水平
若做导弹武器射程鉴定的全面试验,共需要34=81次试验,次数太多,实际不允许,且试验数据的统计分析较复杂.
针对以上问题,本文考虑用多因素试验的设计方法之一——正交试验设计来讨论.
2.2 正交表及正交试验方案
针对导弹武器射程评估的多因素试验问题,试验设计方法众多,研究的基本内涵是如何制定试验方案使导弹试验次数尽可能少,并使试验结果能有效地进行统计分析,最终目的是分析因素对导弹射程是否有显著影响或寻找较优(或最优)试验方案.目前具有代表性的试验设计方法之一是正交试验设计,它是利用一套规格化的表格——正交表来安排多因素多水平试验,并对试验结果进行统计分析,找出较优(或最优)试验方案的一种科学方法.下面先对正交试验设计进行简要的介绍.
2.2.1正交表介绍
同水平的正交表形如Ln(tm)(如下表2是一张L9(34)正交表),其中L表示正交表符号;n表示正交表行数,即正交表安排试验的次数;m表示正交表列数,即最多可安排因素的个数;t表示每个因素的水平数.
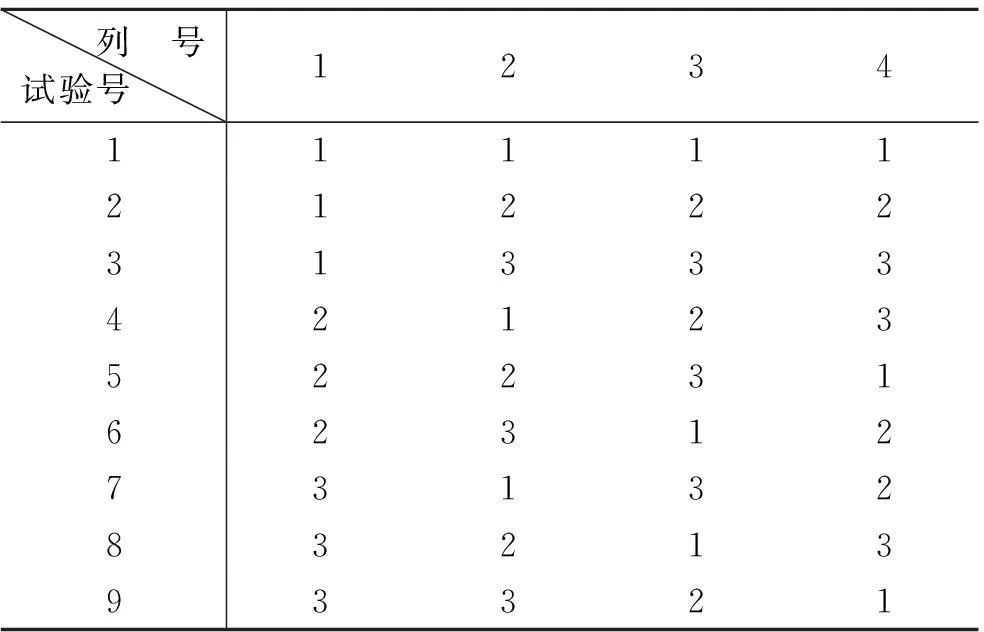
表2 L9(34)正交表
正交表的两个基本特征是:
(i)整齐可比性:每列中各种水平出现的次数相同;
(ii)均衡搭配性:任意两列中横向间所有各种“数对”出现的次数相同,且各种搭配都出现,是全面搭配,一般分类同水平的正交表、混合正交表以及交互作用列表三大类[1-2].关于正交表的构造,在正交拉丁方的基础上运用组合数学理论而形成,参见文献[2].
2.2.2正交试验方案
正交试验设计的任务之一是用正交表确定试验方案.对于问题,关心的导弹射程,所考察四个因素(假定因素间无交互作用)

要寻找影响导弹射程的主要因素,需要用正交表安排试验:
(i)选一张合适的正交表:在三水平正交表中考虑,如用L9(34)(也可用L27(313)[2]);
(ii)表头设计:将因素A,B,C,D依次填入L9(34)的1~4列上(原则上是随机填入),各因素的水平与L9(34)中因素所在列的水平对应起来,得表2.这就完成了表头设计(注:此处是无交互作用情形的表头设计).由此表确定了试验方案,即从全面试验的81次中只选9次进行试验,如第6号试验条件:
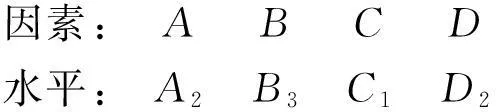

表3 正交表L9(34)实施方案
一旦试验方案确定,严格按各号试验条件进行试验,得表3,最右侧的导弹射程数据yi,i=1,2,…,9.
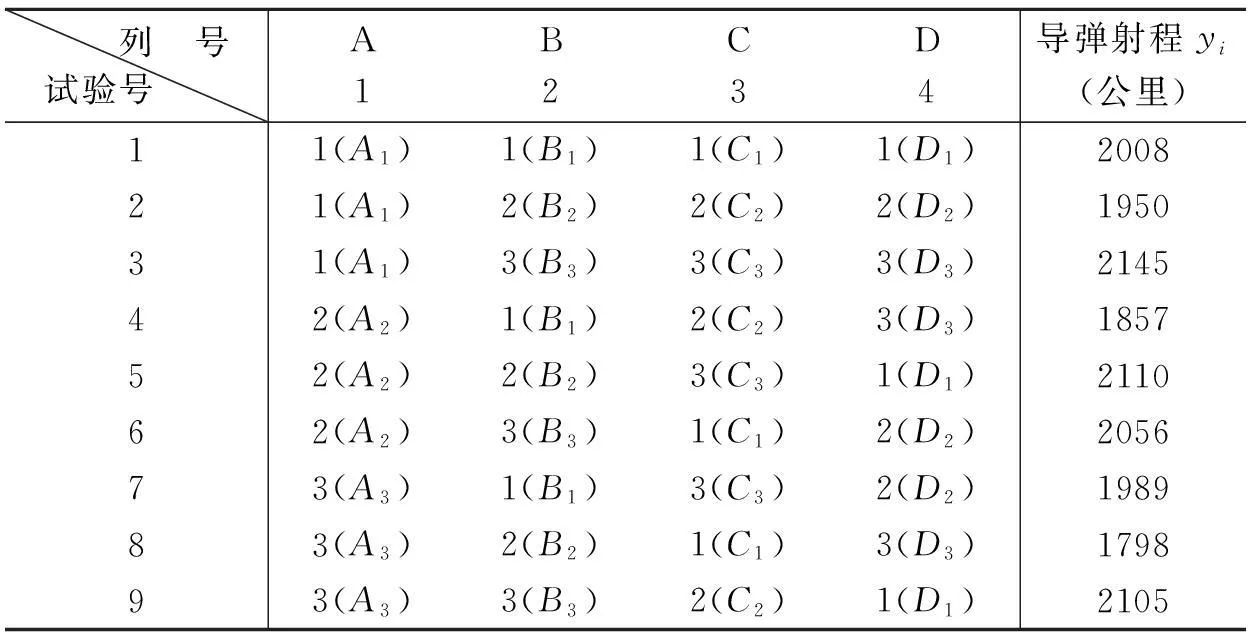
表4 由正交表L9(34)实施的导弹射程试验

图1 L9(34)正交表试验方案的示意图
2.2.3正交试验方案的合理性解释
用正交表制定试验方案,可大大减少试验次数,且试验点具有很好的代表性.例如:对于问题一中,假设只考虑三个因素A,B,C(假定因素之间无交互作用)的影响,每个因素各取三个水平,分别记为
A: A1,A2,A3; B: B1,B2,B3;C: C1,C2,C3
决定进行试验以寻找较好组合方式.若进行全面试验需做33=27次试验,如图1所示立方体上的各条线的交点表示了这27个试验条件.若用正交表安排试验,选L9(34)较合适,如用L9(34)的前三列分别安排因素A,B,C,则只需安排9次试验,且这9个试验点“·”很均匀地分布在立方体的各个部位,可以说是面面俱到,线线俱到.在上、中、下,左、中、右,前、中、后的九个面的每个面上均衡整齐地分布着三个试验点,在27条线上,每条线上分布一个试验点,非常均匀.这是正交表的两个特征所决定的,可以说用正交表安排的这9个试验点能很好地代表27个试验点[3].
3正交试验的数据分析——极差分析法
对于导弹射程评估的正交试验方案下的试验数据(见表3的最右侧),随后进行数据分析以获得最优决策,常用方法有极差分析法与方差分析法[1].极差分析法:直观、简单,但过于粗糙,未能深入考虑试验误差的大小;方差分析法:结论更精确,但理论深刻,计算量稍大.下面仅讨论极差分析法[4].
3.1 数据计算
将问题中实弹测试的结果(见表3)y1,y2,…,y9按每列的同水平分别求和,得到数据和Ij,IIj,IIIj(对应第j列的“1”,“2”,“3”水平),并计算极差
Rj≜max{Ij,IIj,IIIj}-min{Ij,IIj,IIIj},j=1,2,3,4
得到极差分析数据表4.

表5 极差分析数据表
3.2 试验因素分析及最优组合方式
首先指出:提高导弹射程(指标yi)是试验的目的,yi越大越好.
关于数据和Ij,IIj,IIIj及极差Rj的直观分析(以j=1为例).
I1反映因素A(第1列所排因素)的“1”水平的三次作用及其它因素(B,C,D)各水平的一次作用;II1反映因素A的“2”水平的三次作用及其它因素各水平的一次作用;III1反映因素A的“3”水平的三次作用及其它因素各水平的一次作用.由此可以认为:
B,C,D三个因素对I1,II1,III1的作用大体相同;I1,II1,III1之间的差异主要由因素A的水平不同所致,且大者为好;R1反映了A的水平变动对导弹射程影响的大小.
同理,I2,II2,III2,R2反映因素B(第2列所排因素)的情况;I3,II3,III3,R3反映因素C(第3列所排因素)的情况;I4,II4,III4,R4反映因素D(第4列所排因素)的情况.分析结论:
(i)因素对导弹射程影响的主次
由Rj(j=1,2,3,4)这一行知作用大小:

B,D,C,A
即燃料(因素B)和空间环境(D)最重要,其次射向(C),而推进器(A)就不太重要了.
(ii)找出较好的生产工艺条件
由各因素的重要地位及Ij,IIj,IIIj,可得较好的组合方式为:
A1B3C3D1
(iii)各因素的水平改变时,指标的变化趋势:
可用因素—指标图描述:对每个因素,以指标(用Ij,IIj,IIIj表示)为纵坐标,因素的水平为横坐标,描点,并连成折线,如图2.
(iv)若希望进一步提高导弹射程,可由图2再做探索性试验.
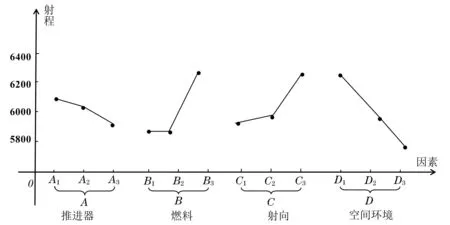
图2 因素-指标图
3.3 导弹射程试验评估基本步骤
导弹射程评估的试验设计方法的基本步骤如下:
Step 1:定试验指标、确定因素、选水平;
Step 2:选用适当的正交表,表头设计,确定试验方案;
Step 3:严格按条件做试验,并记录试验结果;
Step 4:计算各列的同一水平的数据和与极差;
Step 5:按极差大小排出因素的主次;
Step 6:选取较好的组合方式;
Step 7:进行验证性试验,做进一步分析.
4结论
本文将正交试验设计的教学内容应用于导弹武器射程评估的实际鉴定中,通过对影响导弹武器射程影响的分析,在确定的水平条件下,进行正交试验设计,得到较好的组合方式.结合理论分析和仿真案例,回答了多因素水平下的导弹射程试验评估问题.正交试验设计方法能很好地解决如下问题:
(i)指出了导弹武器射程评估中影响其射程的各因素的主次关系,并进行了排序分析;
(ii)通过不同的组合方式,结合正交试验,得到了最优的因素间的组合模式;
(iii)利用因素-射程图能指出因素与射程的关系,即每个因素水平的改变,导弹射程是怎样变化的;
(iv)利用因素-射程图还可探索进一步试验的方向.
值得注意的是,本文仅考虑了各因素间无交互作用下的正交试验设计方法.然而,在实际应用中,往往存在各因素交互作用,此时的试验设计方案需要进一步分析和研究.
[参考文献]
[1]吴翊, 李永乐, 胡庆军. 应用数理统计[M]. 长沙:国防科技大学出版社,1995.
[2]子胥. 正交表的构造[M]. 济南: 山东人民出版社, 1978.
[3]赵选民. 试验设计方法[M]. 北京: 科学出版社, 2010.
[4]任露泉. 试验设计及其优化[M]. 北京:科学出版社, 2009.
Multi-Factor Orthogonal Experiment Design for
Missile Weapon’s Range Evaluation
HUQing-jun,WANGJiong-qi
(Department of Mathematics and System Science, College of Science,
National University of Defense Technology, Changsha 410073, China)
Abstract:Teaching ideology, teaching mode and method based on problem driven is the trend for the current teaching innovation and development. Taking the evaluation for missile range as the research object, the course teaching for orthogonal experiment design and its application is discussed in this paper. Firstly, the influence factor for missile range is analyzed, and then the orthogonal experiment is designed under the given test levels. Moreover, the optimum combination mode is obtained based on the relationship between factor and index. Multi-factor and multi-level experiment evaluation is researched both from theory analysis and simulation. The problem-driven teaching mode is propitious to enhance study interest and enthusiasm. Besides, the cogitation and comprehension ability can also be strengthened.
Key words:problem driven; experiment design; multi-factor; missile range
[基金项目]国防科技大学研究生数学公共课一流课程体系建设项目
[收稿日期]2014-10-16
[中图分类号]G642.0
[文献标识码]C
[文章编号]1672-1454(2015)02-0066-06

