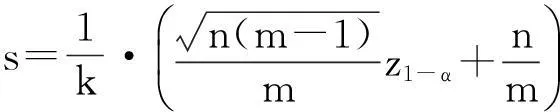案例式中心极限定理教学研究
陈学慧,赵鲁涛,张志刚
(北京科技大学数理学院,北京100083)
案例式中心极限定理教学研究
陈学慧,赵鲁涛,张志刚
(北京科技大学数理学院,北京100083)
[摘要]以案例教学法作为中心极限定理教学的主要手段,选取贴近实际生活的案例——合理规划用电问题和竞争问题,作为教学切入点,激发学生学习兴趣,引导学生从实际情景中发现问题解决问题.课堂实践表明,案例式教学加深了学生对中心极限定理的理解和应用,开阔了学生视野,并对促进课堂教学,课程建设,师生能力提高都有重要意义.
[关键词]中心极限定理; 竞争问题; 正态分布; 案例式教学
1引言
概率论与数理统计是研究探索客观世界随机现象规律性的一门数学学科,它以随机现象为研究对象,是现代数学的重要分支,在金融、保险、经济与企业管理、工农业生产、医学、地质学、气象与自然灾害预报等诸多领域都起着非常重要的作用[1].作为概率论与数理统计课程中一个非常重要的定理,中心极限定理在概率论与数理统计的知识体系中起着承上启下的作用,数理统计中大多统计方法基本以中心极限定理为理论基础.利用中心极限定理,自然界与生产中许多纷乱复杂的随机变量序列和的分布可以利用正态分布近似,而正态分布有着许多重要完美的结论,从而可以获得普遍适用的统计分析方法和结论.中心极限定理有着广泛的实际应用背景,在数理统计、管理决策、近似计算以及保险业等诸多领域中有着重要的应用价值.
中心极限定理是概率论与数理统计学科教学中的一个难点,学生难以短时间内理解,为了使学生掌握定理并能很好的运用定理解决问题,不少教师在其教学方法上进行了探讨.案例式教学是教学改革的有效方式[2],它不同于传统的教学方法,是一种以案例为基础的教学,教师在教学中扮演着设计者和激励者的角色,引导激发学生积极参与分析问题和解决问题,加深学生对中心极限定理的理解和应用.本文将重点研究如何选取贴近现实生活的实例,并按照“案例导入、提出问题、分析求解和思考拓展”的顺序, 由易而难、逐渐深入的对相关模型和应用进行讲授分析.
2案例导入
案例1(住宅小区用电规划问题)城市设计院对某住宅小区设计时估算用电负荷,设该小区有300户居民,晚5∶30-7∶30每户居民使用电器总功率Xi~U(1,3) (单位:kW), 则该小区用电负荷设计至少多大才能以0.99的概率保证居民正常用电?
引导学生分析设用电负荷设计为hkW,记Y为该小区总电器功率(单位:kW),则
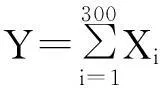
(1)
注意到 X1,X2,…,X300相互独立,即由
P{Y≤h}≥0.99,
求h.于是,需要知道300个独立的随机变量和的分布,那么这大量随机变量和的分布该如何计算呢?
案例2(竞争问题)假设北京与广州之间有两个不同航空公司的航班,两个航班的机型、出发到达时间及价格都相同. 现假定有500位乘客选乘哪一航班是相互独立且是等可能的,且飞机的成本入座率是75%,问飞机设置多少座位可使航班亏损的概率控制在0.05?
引导学生分析记X为500人中选乘某航班的人数,设飞机设有s个座位.由题意,由P{X<0.75·s} =0.05,求s,注意到X服从二项分布B(500,0.5),但直接求s计算非常复杂,无法求出.若将X看成500个两点分布的和,那么大量随机变量和的分布的极限分布会是什么分布呢?
案例3(观察实验)
(i) n个独立同均匀分布的随机变量的和的分布

图1 独立同均匀分布的随机变量的和的分布图
(ii) n个独立同泊松分布的随机变量的和的分布

图2 独立同泊松分布的随机变量的和的分布图
引导学生观察两组分布图,直观地看出独立随机变量和的分布的趋向——正态分布.
3提出中心极限定理
中心极限定理研究的是在什么条件下,独立随机变量和的极限分布是正态分布.为使学生真正理解中心极限定理的内涵,解释以下四个问题:
(i) 为什么中心极限定理研究和的极限分布,而不是精确分布?
(ii) 为什么独立随机变量和的极限分布是正态分布,而不是别的分布?
(iii) 如何描述极限分布是正态分布?
(iv) 为什么称为中心极限定理,这个“中心”是什么意思?
3.1 列维-林德贝格中心极限定理
(ii)∀i,E(Xi)=μ,D(Xi)=σ2,0<σ2<∞.

(2)
并具有应用形式

(3)
或者

(4)
3.2 隶莫佛-拉普拉斯中心极限定理


(5)
一般在实际应用中, 若X~B(n,p),当n较大时, 可使用如下近似公式
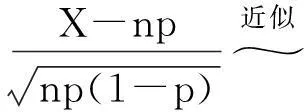
(6)
或者

(7)
4分析求解
案例1求解因为Xi~U(1,3),所以EXi=2,DXi=1/3,可以求得
EY=600,DY=102,
由列维—林德贝格定理知

因此
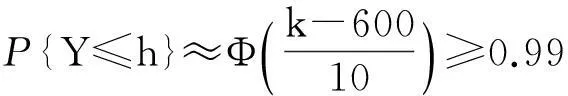
查表得Φ(2.33)=0.9901,求得h≥623.3,即该小区用电负荷设计至少为623.3千瓦时,才能以0.99的概率保证居民正常用电.
案例2求解因为X服从二项分布B(500,0.5) 易算得:
EX=250,DX=125,
由中心极限定理知

因此
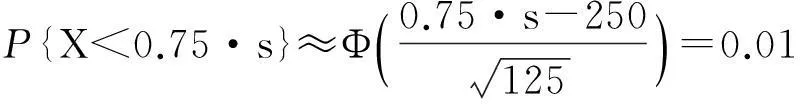
从中解得s≈309.即航空公司选购309个座位的飞机,可使入座率小于75%的概率控制在0.05.
5Matlab实现与拓展思考
利用Matlab软件强大的计算功能,得到座位数s与损失概率

的函数关系α=f(s),如图3所示:
图3中,横坐标为设置座位数,纵坐标为损失概率,显然随着座位数的增多,飞机亏损的概率严格单调递增,在座位数333附近的区间(309,358)内数值变化剧烈,正好符合正态分布“中间大两头小”的特性.随着座位数的减小,损失的概率趋于0.

图3 座位数与亏损概率函数关系图
思考拓展1飞机座位越少越好吗?
分析不是.座位少可能引起乘客人员的损失,所以应该是在飞机控制在较低亏损可能性的情况下,使飞机的收益最大化.让同学课后思考,比较普通的空客客机A330与南航巨无霸A380,在竞争中,谁盈利的可能性更大.
思考拓展2同一航线上如果有多个航空公司竞争,如何设置飞机座位?
分析设有m个航班竞争n位乘客,航班的成本入座率为k, 选乘某个航班的顾客数X服从二项分布B(n, 1/m),航空公司给定一个亏损风险a, 座位数设为s, 据题意:由
P{X 求 s. 由中心极限定理知 所以有 (8) 进而得到s=g(α,k,n,m)关系式为 (9) 当给定α=0.05, k=0.75, n=1000 时,计算出s=g1(m)如图4所示. 图4 座位数s与航班数m的函数关系图 由此可以看出,竞争者增多,只要机型选择适当,仍可保证航班的盈利.引导学生思考类似问题,比如某地区多家电影院竞争观众的座位设置问题以及某区域幼儿园的规模设置问题等. 6结论 案例式教学研究中,城市用电规划问题和竞争问题是我们生活中常见问题.采用中心极限定理来解决上述问题,引导学生对实际问题进行观察分析,建立实际例题与中心极限定理之间的联系,获得实用而简单的统计分析方法和结论.实际上,生活中有许多事物,都可以用概率的眼光去发现研究.通过对实例的分析,意在培养学生自觉主动地用课堂上悟到的思想去分析他所见到的,培养学生的数学素养,是大学数学教师的责任和追求. [参考文献] [1]范玉妹,王萍,汪飞星,李娜.概率论与数理统计[M]. 2版.北京:机械工业出版社,2012. [2]徐群芳.《概率论与数理统计》课堂教学的探索与实践[J]. 大学数学,2010,26(1):10-13. The Study on Case-based Teaching Method of Central Limit Theorem CHENXue-hui,ZHAOLu-tao,ZHANGZhi-gang (School of Mathematics and Physics, University Of Science and Technology Beijing, Beijing 100083, China) Abstract:An actual case is chose for central limit theorem by case-based teaching method, which is the issue on reasonable planning of electricity usage and the competitive consideration. Moreover it will motivate the interests of students and guide them to find and solve problems. Practices in class indicated that case teaching method deepened the comprehension on central limit theorem, widen their views. It has important significance for the improvement of class teaching, curricula construction and capacity improving of teachers and students. Key words:central limit theorem; the problem of competition; normal distribution; case-based teaching [基金项目]北京高等学校青年英才计划项目(YETP0386) [收稿日期]2015-02-15 [中图分类号]O21 [文献标识码]C [文章编号]1672-1454(2015)02-0114-05