超球面上的切触有理插值
许 艳,郭清伟
(合肥工业大学数学学院,安徽合肥230009)
超球面上的切触有理插值
许艳,郭清伟
(合肥工业大学数学学院,安徽合肥230009)
[摘要]给定单位超球面Sd-1上n+1个点及其对应的参数值和其中n个点处的导向量,基于向量的Samelson逆,构造了广义逆向量值有理函数.证明了所构造的向量值有理函数为[2n,2n]型,在指定的参数值处插值于所给点及其导向量,且向量值有理函数位于超球面上.为了说明方法的有效性,给出了数值实例.
[关键词]超球面; 超球面上插值; Samelson逆; 向量值有理函数
1引言
因为多项式函数和有理多项式函数已是工业应用中曲线曲面表示的标准形式,所以大多数的计算机辅助设计系统都采用参数多项式或参数有理多项式表示曲线曲面.由于在计算机辅助设计、计算机图形学中经常要用到二次曲线曲面,二次曲线曲面的有理参数表示曾受到学者们的关注.同样,对在球面上或一般的二次曲面上取定的一列点及其指定的参数值,如何构造位于相应曲面上的向量值有理插值曲线,也是人们通常考虑的问题.进一步,又有人考虑对于球面的情形,这个问题能否推广到超球面上.1986年,Piegl在文献[1]中证明了球面片可以用参数有理Bézier面片精确表示.文献[2]给出了单位球面上任一条不可约有理Bézier曲线和任一片不可约有理Bézier曲面片的显示表示式,并把这一结果推广到椭球面、双曲面、抛物面的情形,证明了若在单位球面上取定互不相同的奇数个点,并给这些点指定不同的参数值,则构造单位球面上的参数有理插值的问题是一个线性问题,且该问题有唯一解曲线.作为文献[2]的后续工作,文献[3]研究了以给定的单位球面上或双曲抛物面上的曲线作为边界线,在相应的曲面上构造有理曲Bézier面片的方法,利用该方法可得到相应二次曲面上的有理参数插值曲线.Anton Gfrerrer[4]把文献[2]的结果推广到超球面的情形,指出在d (d>3)维欧式空间Ed中的超球面Sd-1上给定n个互不相同的点及其对应的参数值,要么存在唯一的在超球面Sd-1上的参数有理曲线在相应的参数值处插值于这些点,要么不存在参数有理曲线,但当所给点的个数为奇数个时,一定存在唯一的参数有理曲线.对给定的单位球面Sd-1(d≥3)上的2n+1个点及相应的参数值,Thierry Gensane[5]基于Samelson逆,构造了Thiele型向量值有理插值式,证明了它是Graves-Morris型(即满足整除性)向量值有理插值,且位于球面上,分子与分母的次数均为2n次.
本文拟解决如下问题:给定单位球面Sd-1(d≥3)上n+1个互不相同的点υ0,0,υ1,0,…,υn-1,0,υn,0及相应的参数值t0,t1,…,tn-1,tn(当i≠j时,ti≠tj)和点υ0,0,υ1,0,…,υn-1,0处的导向量υ0,1,υ1,1,…,υn-1,1,构造参数向量值有理函数R(t),其满足R(ti)=υi,0,i=0,1,…,n,R′(ti)=υi,1,i=0,1,…,n-1,且R(t)位于Sd-1上.R(t)也称为超球面上的切触有理插值函数.
2广义逆向量值有理函数的构造
下面给出R(t)的构造过程.令
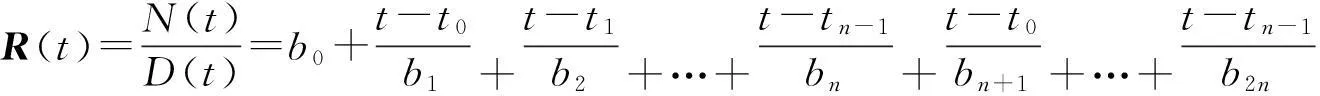
(1)
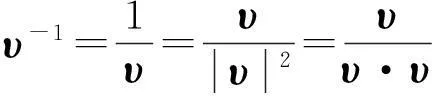

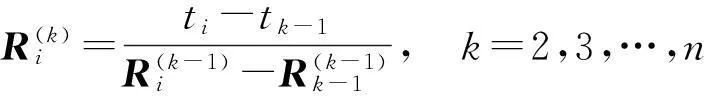

再确定余下的d维向量bn+1,bn+2…,b2n.
对(1)式求导,得

(2)
将ti(i=0,1,…,n-1)带入(2)式,令R′(yi)=υi,1,得
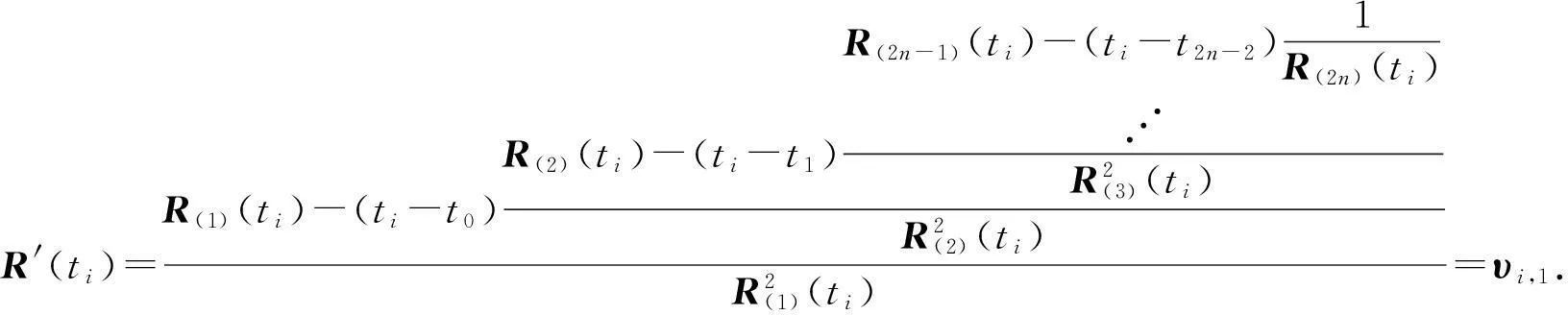
(3)

(4)
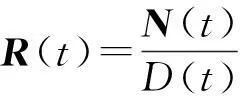
(i) R(tn)=υn,0,R(j)(ti)=υi,j,i=0,1,…,n-1,j=0,1;
(5)
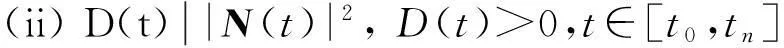
(6)


3主要定理的证明
为证明上节中的定理,先引入以下引理
引理[6]设b0,b1,…,bn,bn+1,…,b2n∈d,ti∈{t0,t1,…,tn},t∈. 如果对向量连分式(1)从末项起逐项向前施行Samelson逆变换,则必存在d维向量多项式N(t)和实多项式D(t)满足

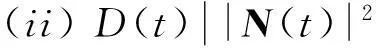
下面给出定理的证明
由b0,b1,…,bn,bn+1,…,b2n的确定过程和引理可得(5)式与(6)式.
由已证明的(6)式知存在多项式Q(t),使得|N(t)|2=Q(t)D(t),即

(7)

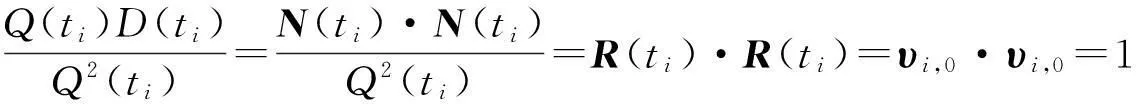
(8)
所以由(8)式得
D(ti)=Q(ti),i=0,1,…,n.
(9)
对(7)式两边关于t求导,得

=2N′(t)·R(t)-D′(t)[R(t)·R(t)].
(10)

Q′(ti)=2N′(ti)·υi,0-D′(ti),i=0,1,…,n-1.
(11)
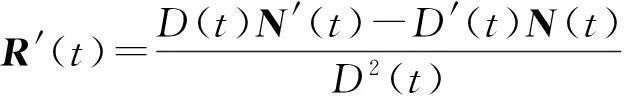
N′(ti)=D(ti)υi,1+D′(ti)υi,0,i=0,1,…,n-1.
(12)
把(12)式代入(11)式右端,得
Q′(ti)=2(D(ti)υi,1+D′(ti)υi,0)·υi,0-D′(ti).
(13)
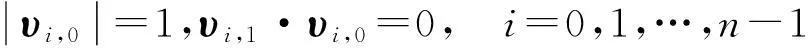
Q′(ti)=D′(ti),i=0,1,…,n-1.
(14)
注由于υi,0,i=0,1,…,n-1是单位球面Sd-1(d≥3)上的点,而υi,1,i=0,1,…,n-1是其导向量,故υi,0与υi,1垂直,从而υi,1·υi,0=0,i=0,1,…,n-1.
由(iii)知
deg|N|2=4n,deg(D)=2n,
所以有
deg(Q)=2n.
(15)
由(9)式、(14)式和(15)式得
D(t)=Q(t).

4数值实例
为说明本文所给方法的有效性,下面给出数值实例.
例1给定单位球面上的三个向量
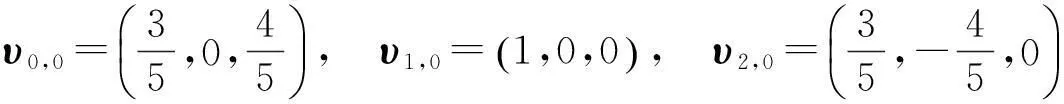
和相应的参数值t0=0,t1=2,t2=4以及υ0,0,υ1,0处的导向量

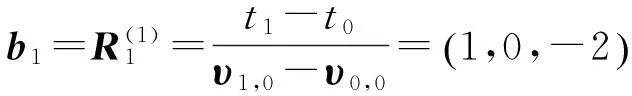
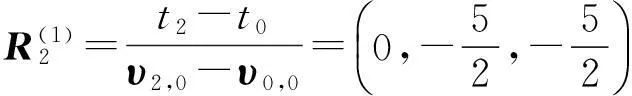


解得


其中
N1(t)=7t4+16t3+t2-60t+108,
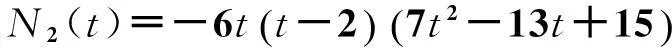
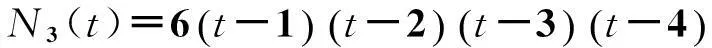
D(t)=43t4-164t3+307t2-276t+180.
R(t)的图形如图1,其中带箭头的线段表示相应点处的切向量.

图1 球面S2上的切触有理插值曲线
例2给定单位球面上的三个向量
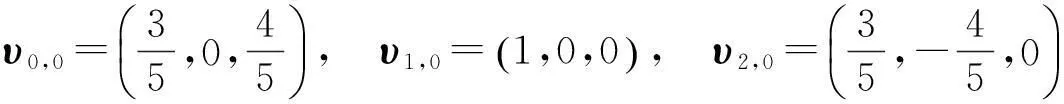
和相应的参数t0=0,t1=2,t2=4以及υ0,0,υ1,0处的导向量

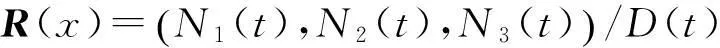
其中
N1(t)=-17t4+472t3-575t2-60t+108,


D(t)=163t4-284t3+307t2-276t+180.
R(t)的图形如图2,其中带箭头的线段表示相应点处的切向量.图3为 例1与例2中球面S2上的切触有理插值曲线的组合.

图2 球面S2上的切触有理插值曲线 图3 例1与例2中球面S2上的切触有理插值曲线的组合
5总结
对给定的单位球面Sd-1(d≥3)上n+1个互不相同的点υ0,0,υ1,0,…,υn-1,0,υn,0及相应的参数值t0,t1,…,tn-1,tn(当i≠j时,ti≠tj)和点υ0,0,υ1,0,…,υn-1,0处的导向量υ0,1,υ1,1,…,υn-1,1,本文给出了求广义逆有理函数的方法,并证明了所得到的广义逆有理函数满足插值条件,且在超球面上.用数值实例说明了方法的有效性.由数值实例可看出,当插值点及其参数相同,但插值点处的切向量不同时,得到的插值曲线也是不同的.关于超球面上更高阶的切触有理插值问题,将另文讨论.
[参考文献]
[1]Piegl L. The sphere as a rational Bézier surface[J]. Computer Aided Geometric Design,1986,3(1):45-52.
[2]Dietz R, Hoschek J. and Jüttler B. An algebraic approach to curves and surfaces on the sphere and other quadrics[J]. Computer Aided Geometric Design,1993,10(4):211-229.
[3]Dietz R, Hoschek J. and Jüttler B. Rational patches on quadric surfaces[J]. Computer-Aided Design, 1995,27(1):27-40.
[4]Anton Gfrerrer. Rational interpolation on hypersphere [J]. Computer Aided Geometric Design,1999, 16(1): 21-37.
[5]Thierry Gensane. Interpolation on the hypersphere with Thiele type rational interpolants[J]. Numerical Algorithms,2012,60(3):523-529.
[6]Graves-Morris P R. Vector-valued rational interpolants I [J]. Numer.ische Mathematik, 1983,42(2): 331-348 .
[7]王仁宏,朱功勤.有理函数逼近[M].北京:科学出版社,2004,133-139.
Osculatory Rational Interpolation on the Hypersphere
XUYan,GUOQing-wei
(School of Mathematics, Hefei University of Technology, Hefei 230009, China)
Abstract:We have created the generalized inverse vector-valued rational function, based on vector’s Samelson inverse when given n+1 points and n derivative vectors on a unit hypersphere Sd-1. We prove that every vector-valued rational function created is a [2n,2n] type and is on a hypersphere, and the given parameter values interpolate in the given points and its derivative vectors. Numerical results are given to prove the effectiveness of the method.
Key words:the hypersphere; interpolation on hypersphere; Samelson inverse; vector-valued rational function
[中图分类号]O241.5
[文献标识码]A
[文章编号]1672-1454(2015)02-0005-05

