关于树指标二阶齐次马氏链的等价定义

季金莉,　石志岩,　杨卫国

(江苏大学理学院, 江苏镇江212013)



关于树指标二阶齐次马氏链的等价定义

季金莉,石志岩,杨卫国

(江苏大学理学院, 江苏镇江212013)

[摘要]树指标随机过程是近年来概率论的研究方向之一，已引起了概率论、物理学、计算机等学科的广泛关注，国内外关于树指标随机过程的研究已经取得了一定的成果.树指标随机过程中的一类重要的模型就是树指标马氏链.Benjiamini和Peres首先给出了树指标马氏链的定义.杨卫国、陈晓雪和王豹给出了树指标一阶马氏链的等价定义.杨卫国等又研究了树指标马氏链强极限定理.为了更有效的研究树指标随机过程，本文给出树指标二阶齐次马氏链的等价定义，并证明其等价性.

[关键词]等价定义; 树; 马氏链; 树指标随机过程

1引言

图1　Gayley树TC,2形成的双根树

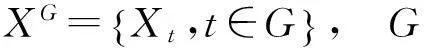
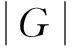
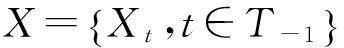
树指标随机过程是用来描述具有树的结构的数据模型，在生物学中有着很好的应用.生物学家研究杆状菌的分裂时，总结出杆状菌分裂的规律，即一个杆状菌在分裂时，从中间断开，这样分裂成两个新杆状菌，这两个新的杆状菌为原来的杆状菌的后代.如果我们把每一次分裂中的杆状菌看成一个顶点，那么所有杆状菌全体就是一个树指标随机过程[1].因此研究树指标随机过程的各种极限理论不仅有较高的理论意义，同时也具有较好的实际应用价值.Benjiamini和Peres[2]首先给出了树指标马氏链的定义并研究了其常返性质和射线常返性质.Berger[3]等研究了齐次树图上平稳随机场熵率的存在性.杨卫国等[4-6]研究了齐次树图上马氏链场状态发生频率，以及二阶有限非齐次马氏链的强大数定律.杨卫国等[7]研究了树指标马氏链的等价定义.石志岩等[8]研究了树上二阶非齐次马氏链随机转移概率调和平均的极限性质.本节我们主要给出树指标二阶齐次马氏链的定义，并研究树指标二阶齐次马氏链若干的等价定义.

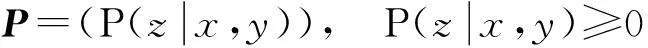
则称P为二阶转移矩阵.

p=(p(x,y)),x,y∈G,

(1)

(2)

分别为G2上的概率分布和G3上的二阶转移矩阵.如果对于任何顶点t,

(3)

且

P(X-1=x-1,X0=x0)=P(x-1,x0),∀x-1,x0∈G,

(4)

2主要结果

给出二阶树指标马氏链的等价定义.

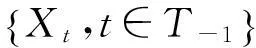
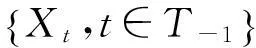
(5)

证(i)→(ii)：由(i)式及条件概率的乘法公式有

=P(X-1=x-1,X0=x0,XL1=xL1,XL2=xL2…XLn=xLn)

(6)

设i≥1,∀t∈Li,有

=…

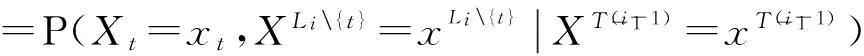
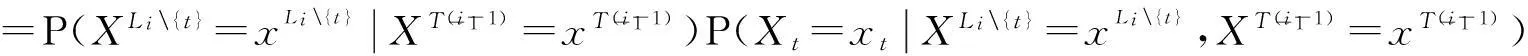
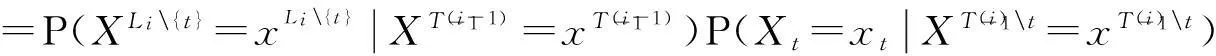
将上式代入(6)中

显然有

P(X-1=x-1,X0=x0)=P(x-1,x0),x-1,x0∈G,

只需要证明，对于任何顶点t,(t≠-1,0)

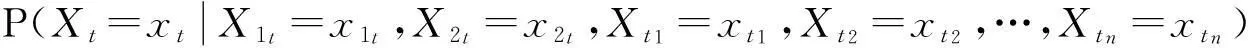
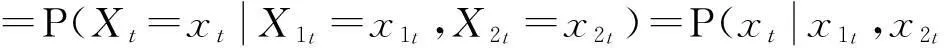
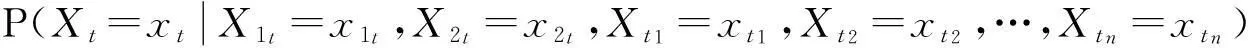
(7)

又

P(X1t=x1t,X2t=x2t,Xt1=xt1,Xt2=xt2,…,Xtn=xtn)

(8)

于是得

即(i)式成立.

注2将(5)式作为二阶齐次马氏链的等价定义.如果t仅和父代1t有关，就是陈晓雪[7]等研究的树指标马氏链等价定义.显然本文t不仅和父代1t有关，而且和祖父代2t也有关系，所以本文将树指标马氏链等价定义的推广到树指标二阶马氏链.类似地，也可以给出树指标高阶马氏链的定义.

[参考文献]

[1]Guyon J. Limit theorems for bifurcating Markov chains[J]. Application to the detection of cellular aging, Ann. Appl.Probab.， 2007, 17 (5-6): 1538-1569.

[2]Benjamini I,Peres Y. Markov chains indexed by trees[J]. The Annals of Probability,1994,22(1):219-243.

[3]Toby B,Ye Z X. Entropic aspects of random fields on trees[J]. IEEE Transactions on Information Theory,1990,36(5):1006-1018.

[4]Yang W G,Liu W. Strong law of large numbers for Markov chains fields on a bethe tree[J]. Statist Probab Lett, 2000,49:245-250.

[5]Yang W G. Some limit properties for Markov chains indexed by a homogeneous tree[J]. Statist Probab Lett,2003, 65:241-250.

[6]杨卫国,刘杰.关于二重有限非齐次马氏链的强大数定律[J].江苏大学学报:自然科学版,2009,30(2):209-212.

[7]陈晓雪,杨卫国,王豹. 树指标马氏链的等价定义[J]. 数学研究,2012, 45(4):411-414.

[8]Shi Z Y,Yang W G. Some limit properties of random transition probability for second-order nonhomogeneous Markov chains indexed by a tree[J]. Journal of Inequalities and Applications,2009,25:65-71.

[9]石志岩,杨卫国.树上非齐次马氏链随机转移概率的极限性质[J].应用数学学报,2008,31(4):648-653.

[10]刘文.有限非齐次马氏链随机转移概率调和平均的一个强极限定理[J].数学物理学报,2000,20(1):81-84.

[11]严加安,测度论讲义[M].北京:科学出版社,2004:107.

The Equivalent Definition of Second-Order

T-indexed Markov Chains

JIJin-li，SHIZhi-yan，YANGWei-guo

(Faculty of Science, Jiangsu University, Zhenjiang 212013, China)

Abstract:T-indexed stochastic processes have been one of the research directions in probability theory,which have draw wide attention of probability theory,physics,computer science and so on in recent years.There have been some works on tree-indexed stochastic processes at home and abroad.Tree-indexed Markov chain is a kind of important model of tree-indexed stochastic processes.Benjiamini and Peres firstly give the definition of Markov chains.Yang,Chen and Wang give the equivalent definition of t-indexed Markov chains.Yang have studied the strong laws of large numbers and Asymptotic Equipartition Property (AEP) for Markov chains field on trees and studied the strong limit theorem of t-indexed Markov chains.In order to study series of related problems about t-indexed stochastic processes efficiently,this paper presents the equivalent definition of second-order t-indexed Markov chains and proves the equivalence of it.

Key words:equivalent definition; tree; Markov chains; T-indexed Markov Chains; tree-indexed stochastic processes

[基金项目]国家自然科学基金资助课题(11071104,11226210); 江苏大学高级人才启动基金(11JDG116)；江苏省教育厅统计应用研究基地；2014年江苏大学统计学校级重点学科

[收稿日期]2014-11-20

[中图分类号]O211.6

[文献标识码]A

[文章编号]1672-1454(2015)02-0010-04