一类两个变量的弱奇性Wendroff积分不等式的推广

刘兴燕，曾德宇

(1.宜宾学院数学研究所，四川宜宾644007；　2.四川省宜宾市第一中学校， 四川宜宾644000;

3. 四川大学电子信息学院， 四川成都610041)



一类两个变量的弱奇性Wendroff积分不等式的推广

刘兴燕1，曾德宇2，3

(1.宜宾学院数学研究所，四川宜宾644007；2.四川省宜宾市第一中学校， 四川宜宾644000;

3. 四川大学电子信息学院， 四川成都610041)

[摘要]建立了一类有两个变量的非线性弱奇性Wendroff型积分不等式解的估计， 所得结果推广了过去关于非线性弱奇性Wendroff型积分不等式的相关结果， 所给出的解的估计更具有一般性.

[关键词]非线性; 弱奇性积分不等式; 解的估计; 两个变量

Key words:quadric surface; tangent line; tangent point; plane nonlinearity; weakly singular integral inequality; estimate on solutions; two variables

1引言

奇异积分不等式是微分方程理论中一个十分重要的部分， 有大批学者从事这方面的理论研究，取得了一系列较好的结果[1-7].特别地， Henry[1]提出了一种估计带有弱奇异核的线性积分不等式解的方法， 他的不等式在研究抛物型偏微分方程中与著名的Gronwal不等式(如文[8-11])在常微方程中一样起着重要的作用. 1997年Medved[2]研究了Gronwall-Bellman-Bihari型和Henry型奇异积分不等式， 2002年马庆华和杨恩浩[3]研究了弱奇性Volterra型积分不等式. 2008年，Ma[4]研究了一类非线性Volterra-Fredholm型积分不等式

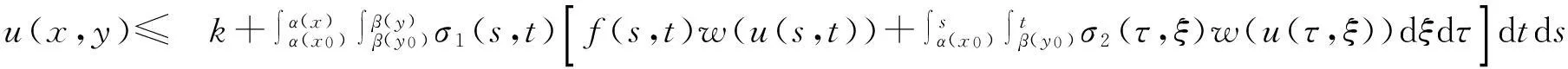
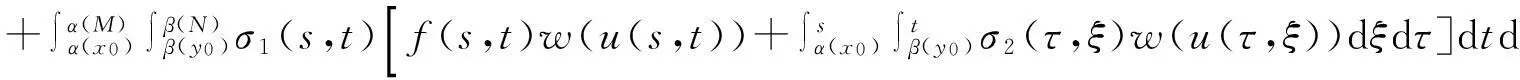
(1.1)

2013年吴宇[5]等研究了一类更广的一类弱奇性Wendroff型积分不等式

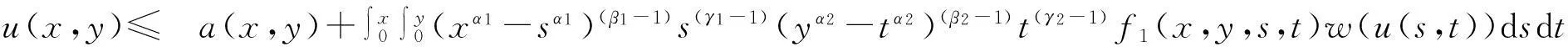
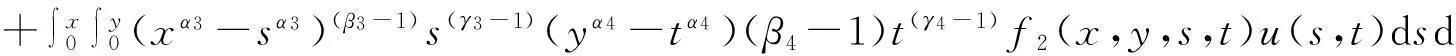
(1.2)

2014年Wang[6]等研究了一类含有两个变量的弱奇性Wendroff型积分不等式

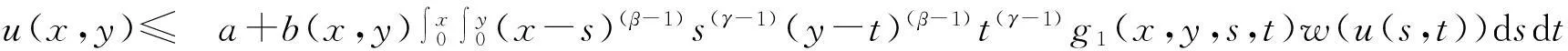
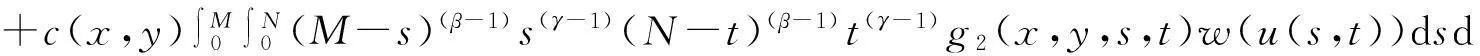
(1.3)

在Wang[6]等工作的基础上， 本文用函数a(x，y)代替(1.3)中的常量a， 考虑更广的一类非线性弱奇性Wendroff型积分不等式

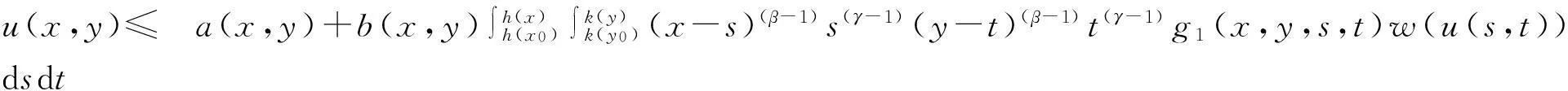
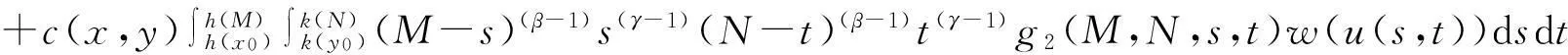
(1.4)

解的估计.

与不等式(1.3)相比，(1.4)式所研究的范围更广， 且函数a(x，y)所满足的条件很简便(可不连续， 不可积)，本文给出解的估计更具有一般性.

2预备知识

为了方便论述，首先引入引理.

引理[3]若α，β，γ，p为正常数， 则

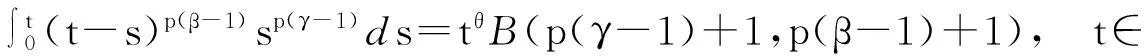
(2.1)

其中B(ζ，η)是Beta函数， 而

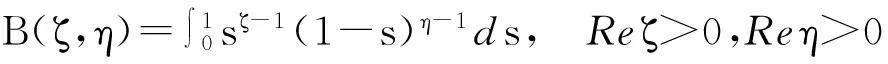
(2.2)

θ∶=p(β+γ-2)+1≥0.

(2.3)

3主要结果

定理如果u(x，y)是定义在(Δ，+)上的连续函数，且满足弱奇性不等式(1.6)， 其中Δ=I1×I2，

I1=[x0，M]，I2=[y0，N]，M≥x0，N≥y0，M，N∈+，

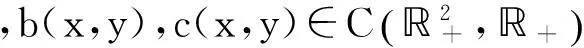
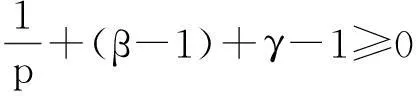
其中p>1且满足p(β-1)+1>0. 则

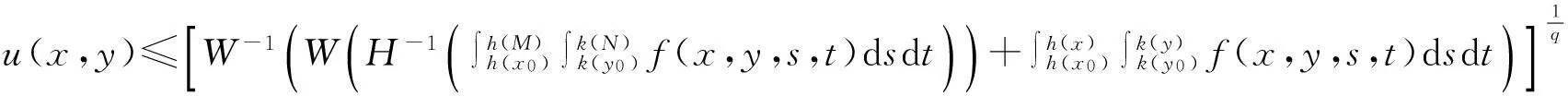
其中

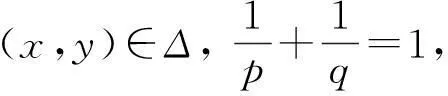
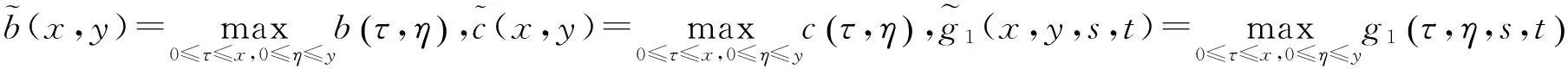
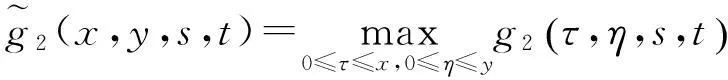
W-1(u)是W(u)的反函数， H-1(u)是H(u)的反函数.

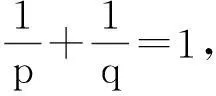
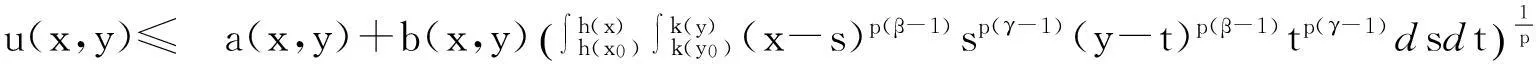
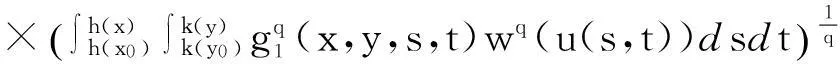
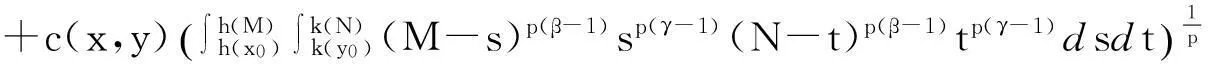
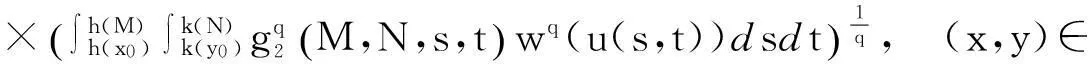
由0≤h(x)≤x， 0≤k(y)≤y，得

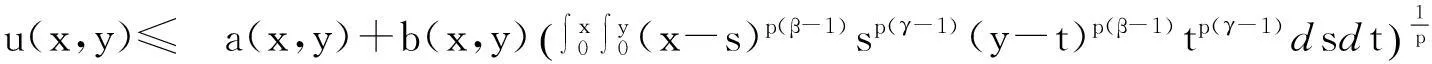
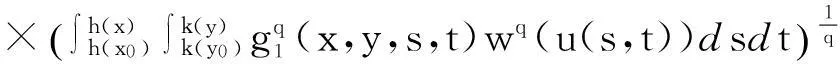
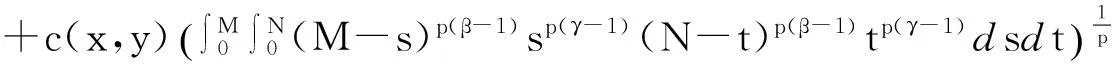
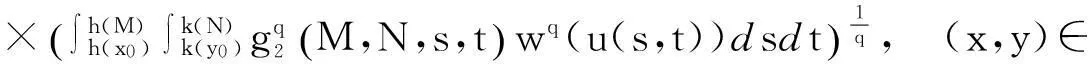
(3.1)

将上式两边q次方， 应用文[2]中不等式“若n为正整数，而r(≥1)，A1，…，An是非负数， 则

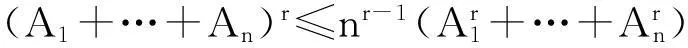
可得

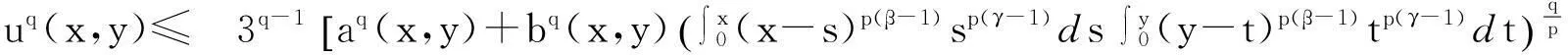
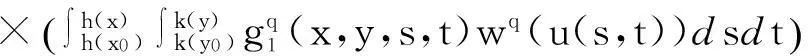
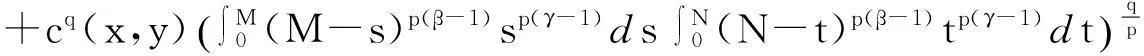
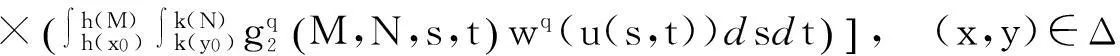
由本文引理及d(x，y)的定义， 得

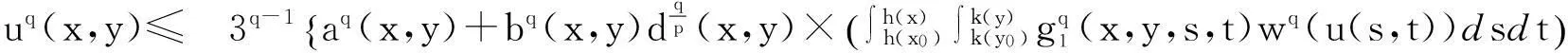
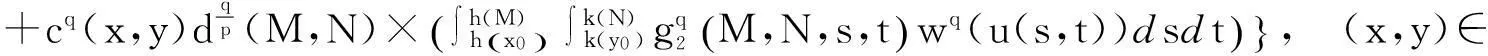
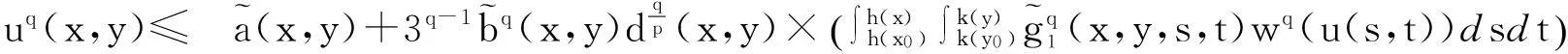
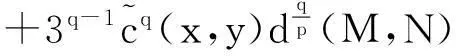
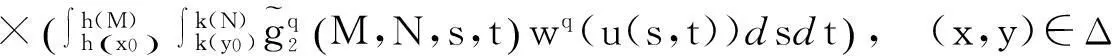
由f(x，y，s，t)的定义有

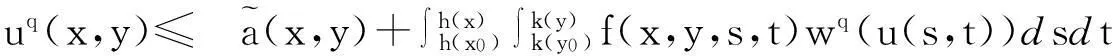
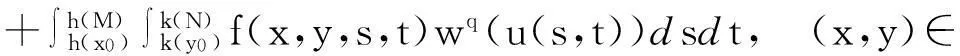
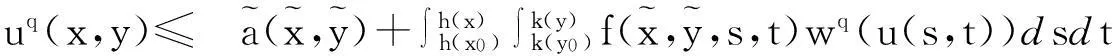
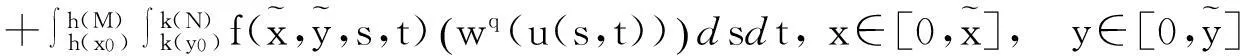
令

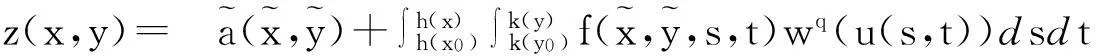
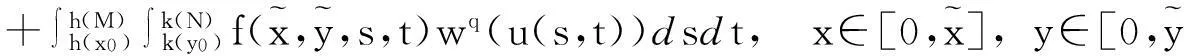
(3.2)

有uq(x，y)≤z(x，y)， 即

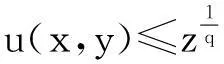
(3.3)

利用函数w(u)关于u单调不减可有

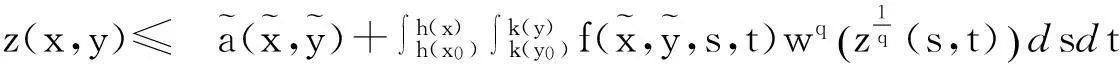
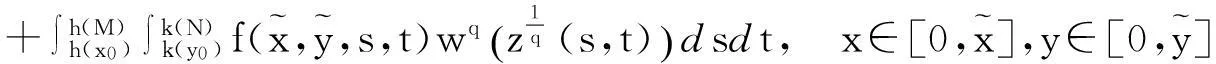
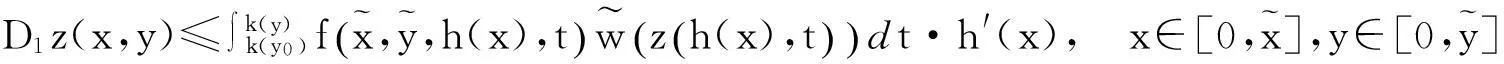
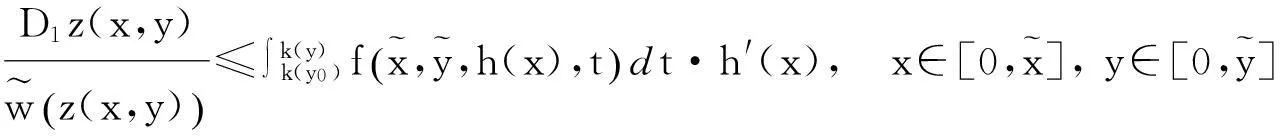
由W(u)的定义， 有

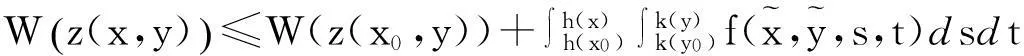
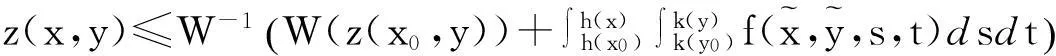
由(3.2)式可得

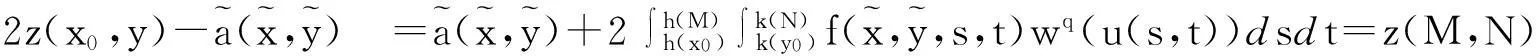
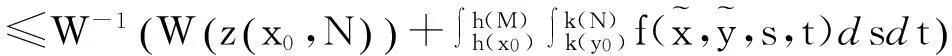
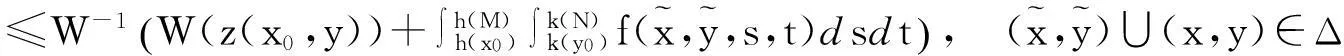
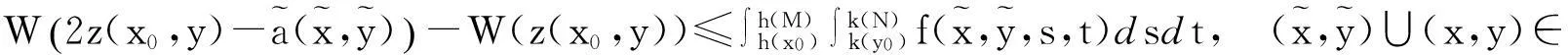
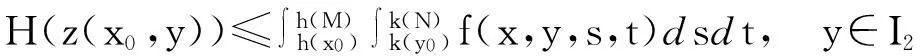
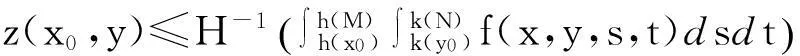
有

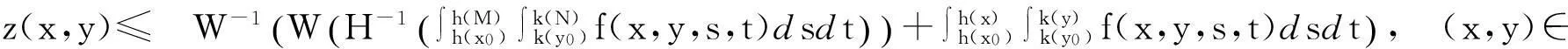
由(3.3)式，得

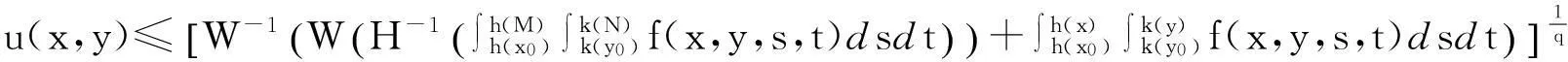
其中(x，y)∈Δ. 定理得证.

注当a(x，y)≡a，h(x)≡x，k(y)≡y时， 才是Wang[6]等所研究的情形.

4在弱奇性微分方程中的应用

若

u(x，y)≤arctan(x+y)

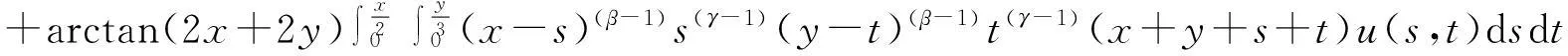
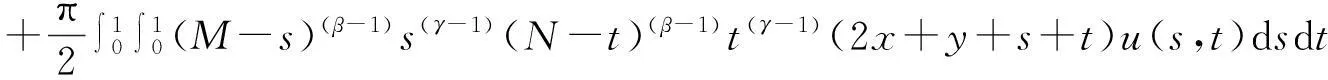
(4.1)

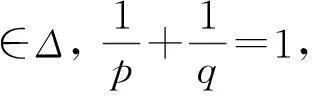
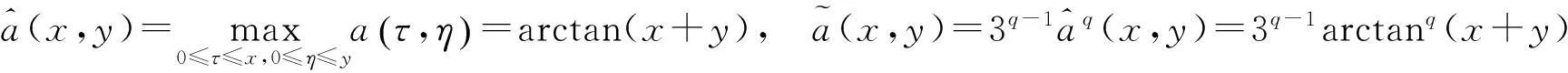
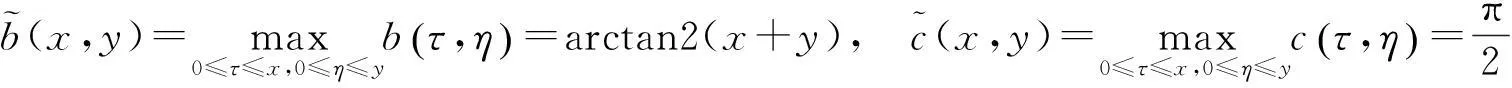
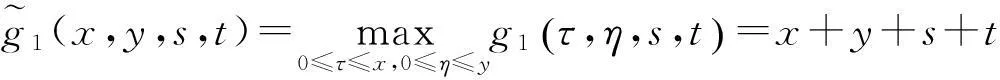
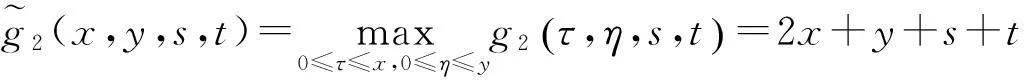
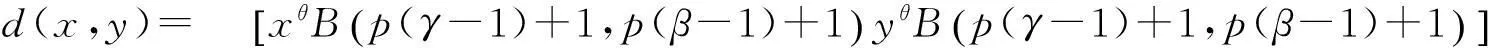
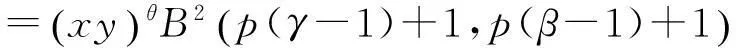
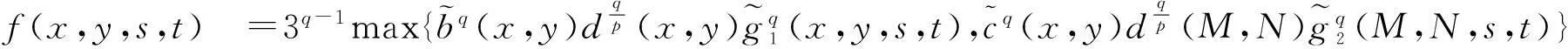
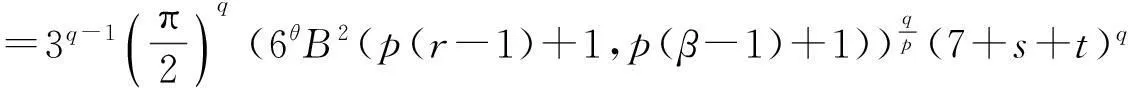
=k(7+s+t)q，

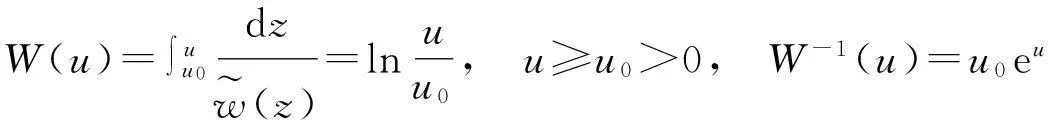
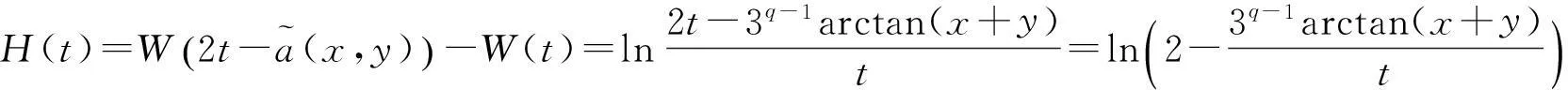
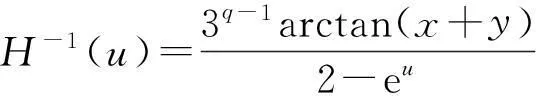
则

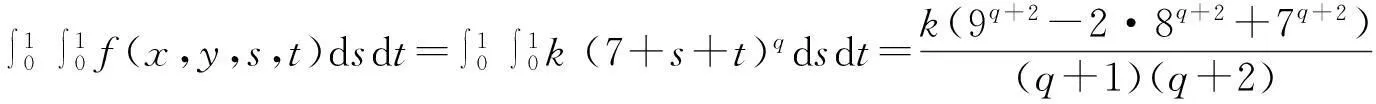
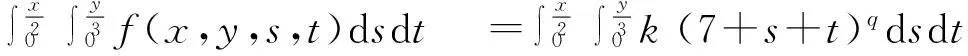
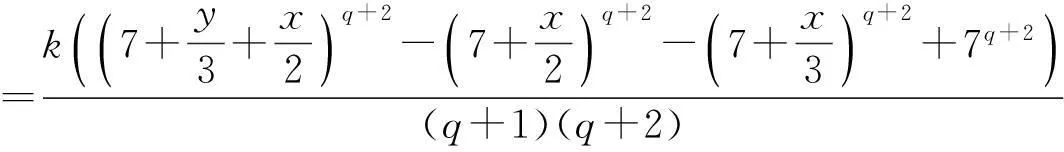
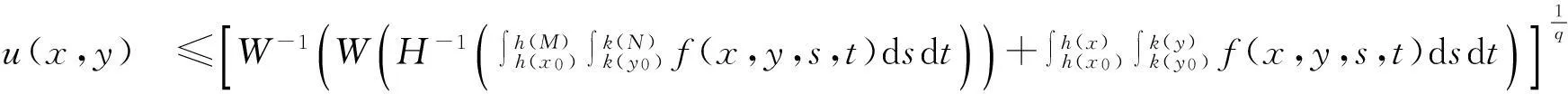
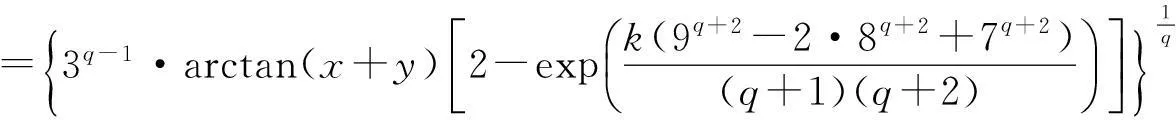
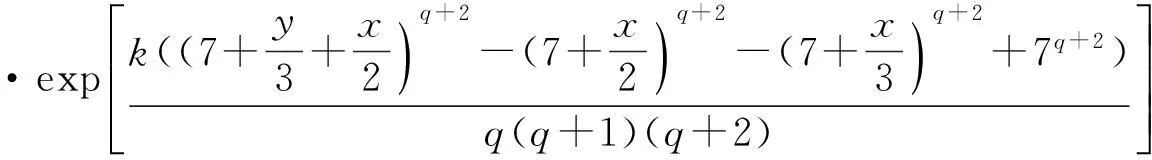
[参考文献]

[1]Henry D. Geometric theory of semilinear parabolic equations [M]. New York: Springer-Verlag， Berlin: Heidelberg， 1981.

[2]Medved M. A new approach to an analysis of Henry type integral inequalities and their Bihari version [J]. J. Math. Anal. Appl， 1997， 214(2): 349-366.

[3]马庆华，杨恩浩. 弱奇性Volterra积分不等式解的估计[J]. 应用数学学报， 2002， 25(3): 505-515.

[4]Ma O H， Josip P. Estimates on solutions of some new nonlinear retarded Volterra-Fredholm type integral inequalities[J]. Nonlinear Analysis， 2008，69: 393-407.

[5]吴宇，唐敏，周察金. 一类新的弱奇性Wendroff型积分不等式解的估计[J]. 应用数学学报， 2013. 36(1): 97-107.

[6]Wang W， Lai Y. A class of nonlinear weakly singularity Wendroff type integral inequality with two variables and application [J]. Advanced Materials Research ， 2014， 1008-1009:1493-1496.

[7]吴宇. 一类新的弱奇性Volterra积分不等式[J]. 应用数学学报， 2008， 31(4): 584-591.

[8]张伟年. 投影下的Gronwall不等式[J]. 数学研究与评论， 1997， 17(2): 257-260.

[9]邓圣福，张伟年. 可积情形下的Gronwall不等式[J]. 数学研究与评论， 2002， 22(2): 307-313.

[10]Zhang W， Deng S. Projected Gronwall-Bellman’s inequality for integrable functions [J]. Math. Comput. Modelling， 2001， 34(3-4): 393-402.

[11]Deng S， Prather C. Generalization of an impulsive nonlinear singular Gronwall-Bihari inequality with delay [J]. J. Inequal Pure and Appl Math， 2008， 9(2): Art. 34， 11 pp. [ Online: http://jipam.vu. edu.au/].

A Kind of Two Variables Weak Singularity Wendroff

Integral Inequality

LIUXing-yan1，ZENGDe-yu22，3

(1. Institution of Mathematical Science， Yibin University， Yibin Sichuan 644007， China;

2. The First High School of Yibin， Yibin Sichuan 644000， China;

3. College of Electronics and Information Engineering， Sichuan University， Chengdu 610041， China)

Abstract:Set up a class of nonlinear weak singularity has two variables Wendroff integral inequalities solution estimates， the obtained results generalize the past type nonlinear Wendroff weak singularity integral inequality related results， is more general solution is given by the estimates.

[基金项目]宜宾学院自然科学重点项目(2012S10)

[收稿日期]2014-12-15

[中图分类号]O178

[文献标识码]C

[文章编号]1672-1454(2015)02-0108-06