一道数学竞赛试题的推广
王 政,尚德生
(山东理工大学理学院,山东淄博255049)
一道数学竞赛试题的推广
王政,尚德生
(山东理工大学理学院,山东淄博255049)
[摘要]对第五届中国大学生数学竞赛决赛(数学类)的一道试题的结论进行了推广,得到了一系列推论.
[关键词]二次曲面; 切线; 切点; 平面
1引言
2014年3月第五届中国大学生数学竞赛决赛(数学类)试题一如下:
该结论其实可以推广至一般二次曲面.
2推广
考虑一般的二次曲面S
Ax2+By2+Cz2+Dxy+Exz+Fyz+Gx+Hy+Iz+J=0.
(1)
曲面外一固定点P(x0,y0,z0),设过定点P的曲面S的切线的方向向量为τ=(u,v,w),则切点Q(X,Y,Z)的坐标可表示为

切点坐标需满足方程(1),则有
A(x0+tu)2+B(y0+tv)2+C(z0+tw)2+D(x0+tu)(y0+tv)+E(x0+tu)(z0+tw)
+F(y0+tv)(z0+tw)+G(x0+tu)+H(y0+tv)+I(z0+tw)+J=0.
化简,得

(2)
其中
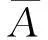

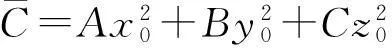
由条件知,(2)式关于t有唯一重根,从而有

(3)
与

(4)
利用(4)式,得
(2Ax0+Dy0+Ez0+G)X+(2By0+Dx0+Fz0+H)Y+(2Cz0+Ex0+Fy0+I)Z
=(2Ax0+Dy0+Ez0+G)(x0+tu)+(2By0+Dx0+Fz0+H)(y0+tv)
+(2Cz0+Ex0+Fy0+I)(z0+tw)
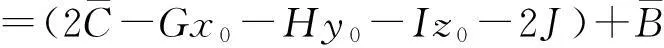

=-Gx0-Hy0-Iz0-2J.
由此可以得到如下结果:
定理过二次曲面S(式(1))外一固定点P(x0,y0,z0)作曲面S的切线,则这些切线的切点均在同一平面上,即
(2Ax0+Dy0+Ez0+G)x+(2By0+Dx0+Fz0+H)y
+(2Cz0+Ex0+Fy0+I)z+Gx0+Hy0+Iz0+2J=0.
x0x+y0y-z-z0=0.

x0x+y0y-z0z=0.
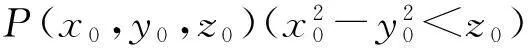
2x0x-2y0y-z-z0=0.

x0x+y0y+z0z=R2.
若S为其他二次曲面,类似可得到相应的结论,在此不再赘述.
[参考文献]
[1]华东师范大学数学系.数学分析[M].4版.北京:高等教育出版社,2010.
On Improvement of a Mathematical Contest Question
WANGZheng,SHANGDe-sheng
(School of Science, Shandong University of Technology, Zibo, Shandong 255049, China)
Abstract:The authors discuss the improvement of a question of a the fifth session of the China Undergraduate Mathematical Contest, and obtain a series of corollaries.
[收稿日期]2014-08-07;[修改日期]2015-01-10
[中图分类号]O172
[文献标识码]C
[文章编号]1672-1454(2015)02-0106-02

