案例教学在《应用随机过程》中的探索和实践

刘秀芹，马　亮，李　娜

(1.北京科技大学数理学院，北京100083;　2.中国科学院数学与系统科学研究院应用数学所，北京100190;

3. 中国科学院动物研究所，北京100101)



案例教学在《应用随机过程》中的探索和实践

刘秀芹1，马亮2， 3，李娜1

(1.北京科技大学数理学院，北京100083;2.中国科学院数学与系统科学研究院应用数学所，北京100190;

3. 中国科学院动物研究所，北京100101)

[摘要]通过C-K方程在推断系统发育树中的应用的角度对案例教学法进行了探索和实践，并在此基础上对应用随机过程的教学进行了几点粗略的探讨.

[关键词]案例教学; C-K方程; 马氏链; 系统发育

1引言

应用随机过程是一门即抽象又与实际紧密结合的学科.笔者在教学过程中强调随机过程在实际中的应用，并结合自身的科研工作情况，把随机过程在科技前沿中的应用案例引入到日常教学过程中来，不但丰富了教学内容，扩大了课堂信息量，而且激发了学生的学习兴趣，提升了学生对抽象理论的理解能力，使学生的思维得到不断攀升.下面仅以切普曼—柯尔莫格洛夫方程的教学为例，在随机过程讲解过程中进行案例教学法的探索和实践.

2切普曼—柯尔莫格洛夫方程的概念及其在推断系统发育树中的应用

齐次马尔可夫链的转移概率矩阵是描述马尔可夫链概率分布的最重要的内容，而切普曼—柯尔莫格洛夫方程是求解转移概率矩阵的桥梁.

2.1　切普曼—柯尔莫格洛夫方程

设{X(t)， t≥0}是连续时间齐次马尔可夫链，以下简称马氏链，pij(t)是该马氏链由状态i经过t时间转移到状态j的转移概率，对任意的s， t，它满足

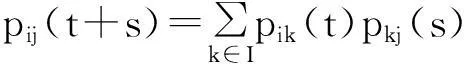
称之为连续时间齐次马氏链的切普曼—柯尔莫格洛夫方程，简称为C-K方程[1].

目前《应用随机过程》的教材中很少提及这一抽象方程在实际中的应用，笔者在进行数学与生物交叉学科的研究过程中发现了C-K方程在推断系统发育树中的应用这一精彩案例.在应用随机过程的讲解过程中采用首先引入抽象的数学公式，然后结合该公式在实际中的应用这一导入式教学法，从而进一步加深学生对这一公式的理解，起到了很好的教学效果.

2.2　C-K方程在推断系统发育树中的应用[2]

生物学家是如何推断人类、黑猩猩、大猩猩之间的系谱关系的呢？

我们知道生物的DNA与RNA序列承载着遗传物质，直观来讲，两个物种之间亲缘关系越近，他们相应的DNA或者RNA序列的差异越小.下面使用人类和猩猩的线粒体12S rRNA数据举例说明如何计算两个物种之间的距离.

经过对人类和猩猩的线粒体基因组12S rRNA序列比对(见图1)，计算出总的位点数和错配的数量分别为n=948和x=90.

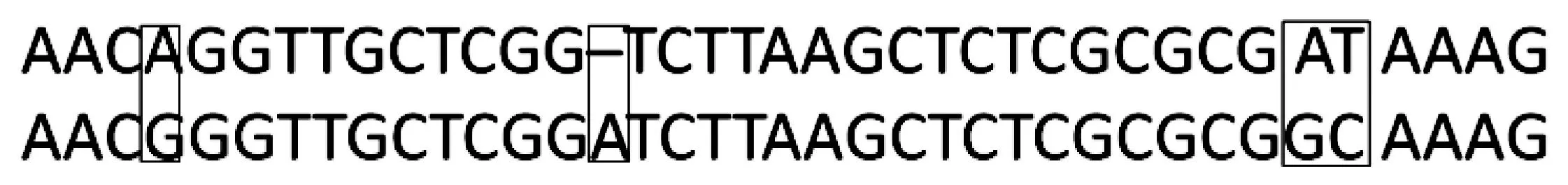
图1　序列比对示意图

如果假设物种变异的速率是固定不变的，那么两个物种分化的时间越长，他们序列中有差异的位点越多，相应地，他们之间的遗传距离也应该越远，从而定义如下距离，即配对距离(又称为错配概率).

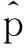
但是错配距离忽略了以下的情况：

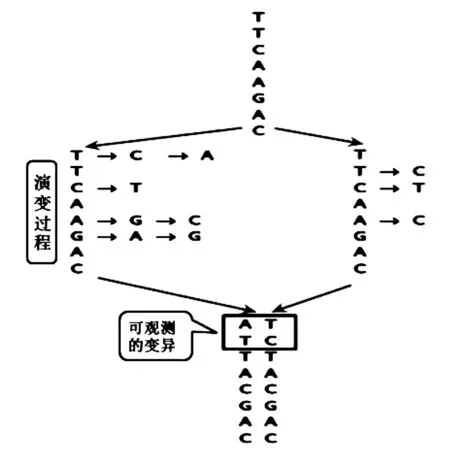
图2　物种序列演变示意图

如图2可见一条祖先序列分化为两条子序列，在整个进化过程中发生了10次碱基替代，但是在两个后代序列中只能观测到两个碱基的变异.

为了考虑不可观测的碱基变异，下面用马氏链模型来描述物种的演化过程，即把每个位点随着时间的变化看成一个连续时间有限状态马氏链{X(t)， t≥0}，其状态空间为S={T，C，A，G}，设它的转移概率矩阵为，

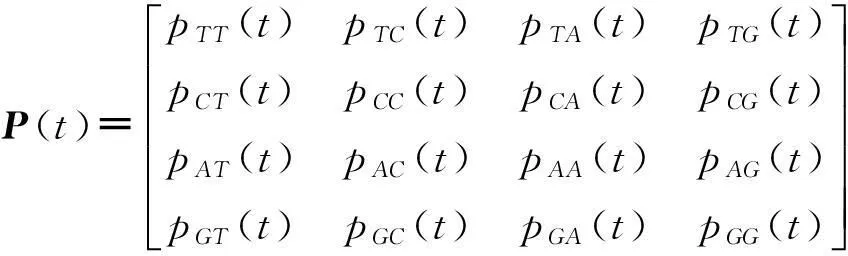
马氏链的转移概率满足切普曼—柯尔莫格洛夫方程：

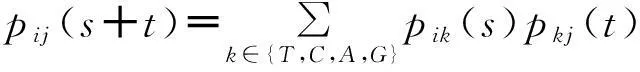
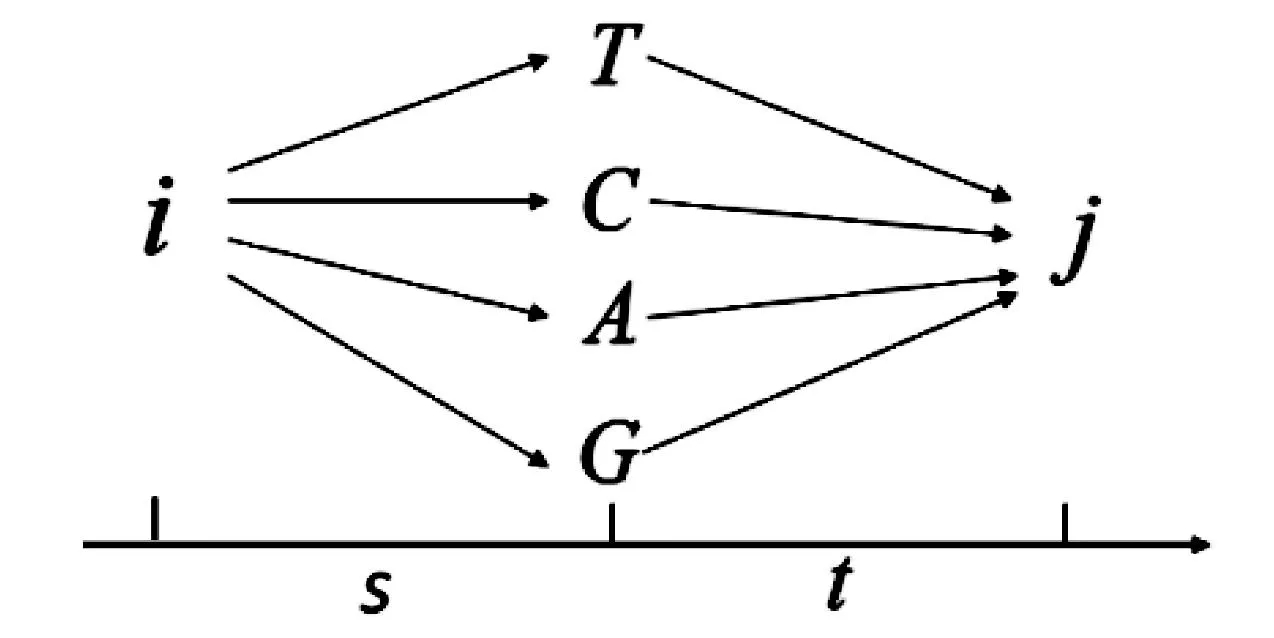
图3　C-K方程时间状态转移示意图

马氏链模型是如何把不可观测的碱基变异(图2)也考虑在内的呢？这主要是因为马氏链从状态i到状态j的转移概率囊括了所有可能发生的进化过程(如图3所示).

在一定条件下，从C-K方程出发可以推出转移概率满足柯尔莫哥洛夫向前和向后方程，

P′(t)=P(t)Q和 P′(t)=QP(t)

(1)

其中Q=(qij)n×n为状态之间的状态转移速率矩阵，qij为状态i替换为状态j的瞬时速率.1969年JukesandCantor[3]给出了一类简单的核苷酸替代模型JC69(式(2)所示)，假设四种碱基有相同的替代速率，

TCAG

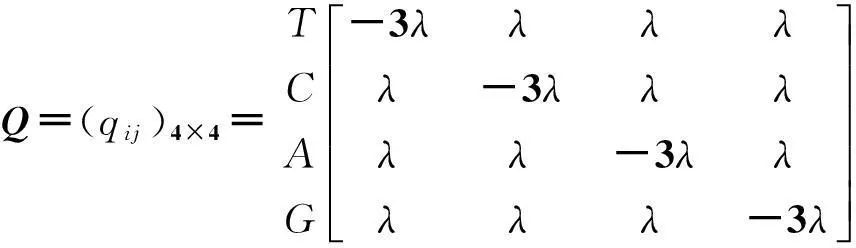
(2)

其中qijΔt表示在很短的时间Δt内状态i转变为状态j的概率.(1)式的解为

TCAG

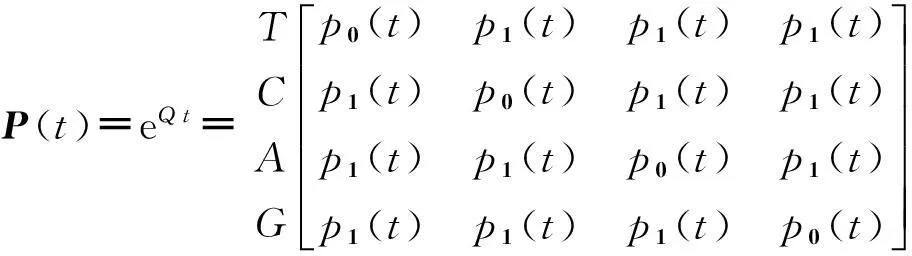
(3)

其中

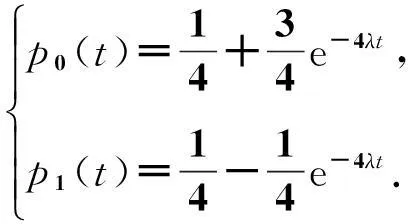
那么我们如何把这个模型应用于矫正两个物种序列之间的距离呢？

显然此马尔可夫链的极限分布为

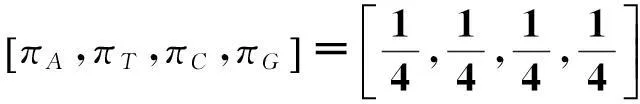
在应用与计算物种间距离的时候，我们一般总是假设过程已经达到平稳状态.

假设两条序列从一个共同祖先发生分歧，经过t/2时间演化到现在的状态(图4 左)，可是我们实际并不知道祖先的状态.由于转移矩阵以及极限分布的对称性，此马尔可夫链是时间可逆的，即对于t≥0，∀i，j∈S有

πipij(t)=πjpji(t).

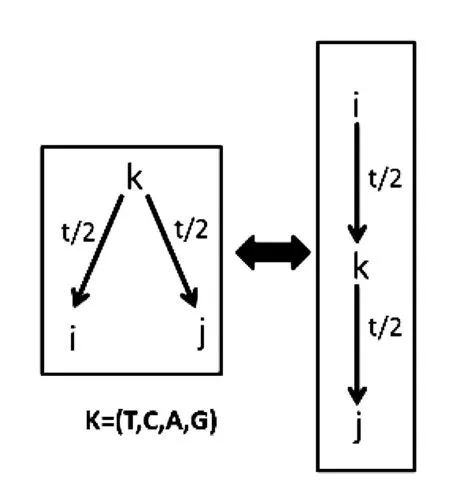
图4

因此我们可以把一条序列视作另一序列的祖先，而把实际的祖先作为中间点，利用C-K方程遍历其所有可能状态(图4右)，

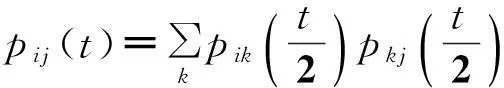
下面估计两条序列之间的距离，从(2)式可见任意一个碱基被其他三种碱基替代的速率总和为3λ，由此两个序列之间的距离可表示为d=3λt， 从而λ=d/3t.

从式(3)可知，两条序列中的碱基变化的概率为

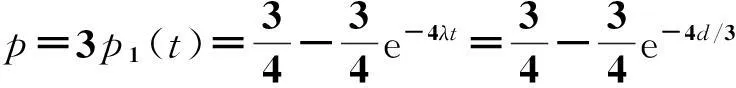
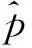
解得

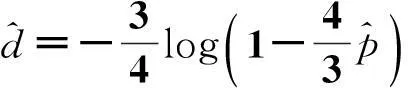
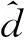
基于物种的线粒体rRNA序列，使用上述方法计算下列物种间的距离矩阵(表1)，从表1可以看到，人类和黑猩猩最近，首先把这两个物种看成一类(A)，使用这一类中各物种与其他类中物种的距离的算数平均值表示类A和其他物种之间的距离(表2).

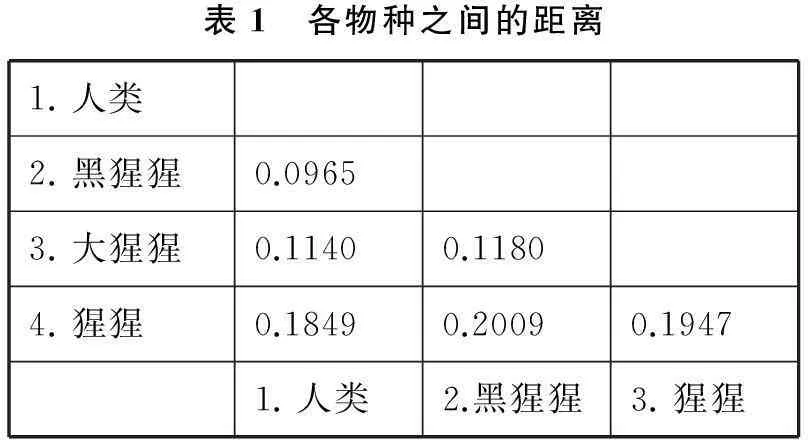
表1 各物种之间的距离1.人类2.黑猩猩0.09653.大猩猩0.11400.11804.猩猩0.18490.20090.19471.人类2.黑猩猩3.猩猩

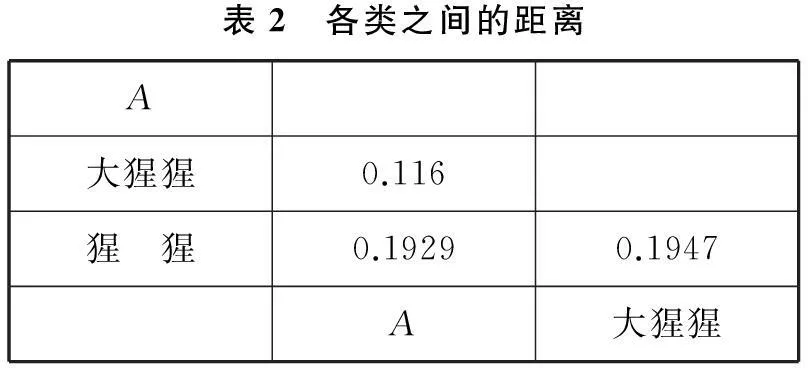
表2 各类之间的距离A大猩猩0.116猩 猩0.19290.1947A大猩猩

如此下去，就构建出了他们之间的系统发育关系(图5)

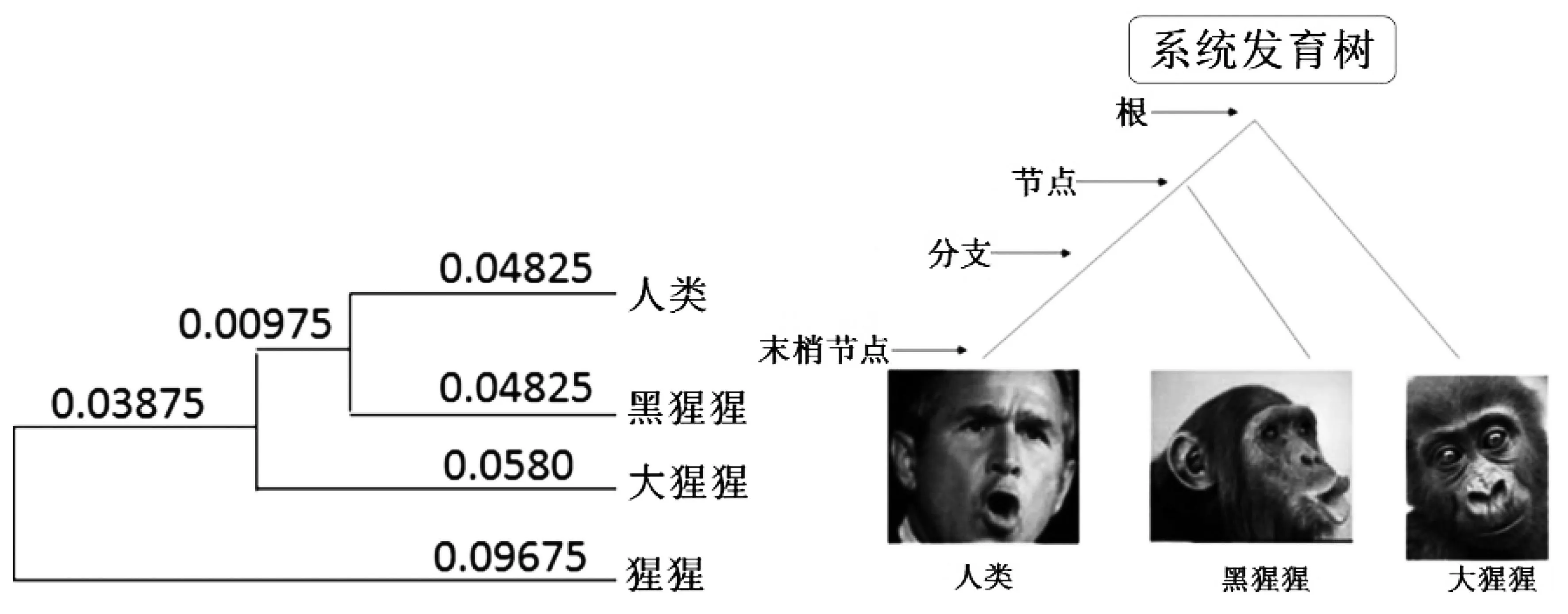
图5　各物种之间的系统发育树及示意图

相比于离散时间马尔可夫链，连续时间马氏链的转移概率及C-K方程的概念更加抽象，计算也更加复杂.通过结合C-K方程在进化生物学中推断系统发育树方面的应用来将抽象的概念具象化，从而加深学生在学习中的理解.

3应用随机过程教学中的几点探讨

3.1　注重由浅入深，结合实际背景讲解基本概念

随机过程是研究自然界中随机现象变化过程的一门学科，它在金融、通信、生物、控制等科学技术领域都有广泛的实际应用.由于研究对象随机性、复杂性的特点，随机过程的概念相对比较抽象.在讲解过程中注重由浅入深，以最朴素的语言介绍随机过程的基本理论和分析方法，通过大量精选例题使学生能够比较容易的理解随机过程的基本概念；采用形象生动的图形展现随机过程的一些关键知识点(例如，随机过程的样本曲线，柯尔莫哥洛夫前进后退方程的时间状态对应示意图等)；讲解基本概念时通常可以将其与具体的应用实例结合起来，使学生更容易接受.例如，对随机过程定义的讲解，可以结合具体的实例，如生物种群的增长问题，手机接收到的电话次数问题，超市的客流量问题等；再如讲到泊松过程的时候，可以结合某盏灯更换灯管的数量；而复合泊松过程的讲解可以结合乘飞机抵达机场的乘客人数，保险公司的保险储备金数量等.

3.2　从案例整合和结合前沿方面构建课程内容

任课教师应该结合自己的科研情况，把随机过程在科技前沿中的应用引入到教学过程中，只有充分考虑当前科学综合、交叉、渗透的发展趋势，做到教学内容不仅能帮助学生理解随机过程最本质的东西，而且能了解各种基本规律之间，各分支之间的联系，同时，将一些知识点组合成为案例，通过研究者的思想、语言和方法，集中传递科学思想.把反映当前科学前沿的内容整合到教学中，给学生逐步走向科技前沿起引领作用.

4小结

在应用随机过程教学过程中尽量穿插一些它在交叉学科中的应用的实例，培养学生的“应用意识”[4]，从而达到为国家输送高质量的优秀人才的目的.

[参考文献]

[1]林元烈.应用随机过程[M].北京：清华大学出版社，2002.

[2]Ziheng Yang. Computational Molecular Evolution[M].Oxford: Oxford University Press， 2006.

[3]Jukes TH, Cantor CR. Evolution of protein molecules[M]∥ln H. N. Munro(Ed). Mammalian protein metabolism. New York: Academic, 1969:21-132.

[4]刘秀芹，赵金玲，范玉妹.剖析马氏链平稳分布的讲解——谈《应用随机过程》教学[J]. 大学数学，2011， 27(4):199-202.

Exploration and Practice of Case Teaching in Applied Stochastic Process

LiuXiu-qin1，MaLiang2，3，LiNa1

(1.College of mathematics and Physics， University of science and technology Beijing， Beijing 100083,China;

2. Institute of applied mathematics， AMSS，CAS， Beijing 100190, China;

3.Institute of zoology， CAS， Beijing 100101, China)

Abstract:We have some exploration and practice of case teaching from the point of view of the application of C-K equation in inferring phylogenetic tree， and then give a simple discussion on the teaching of Applied Stochastic Process.

Key words:Case Teaching; C-K equation; Markov Chain; phylogenetic tree

[基金项目]北京科技大学研究型教学示范课项目(KC2014YJX36)；北京科技大学研究生教育发展基金；北京科技大学教研基金(JG2012M38)

[收稿日期]2015-01-03

[中图分类号]O211.6

[文献标识码]C

[文章编号]1672-1454(2015)02-0101-05