矩阵迹的妙用

贾利新

(信息工程大学理学院，郑州450001)



矩阵迹的妙用

贾利新

(信息工程大学理学院，郑州450001)

[摘要]通过例子论述了矩阵迹在特征值问题、行列式计算以及矩阵性质证明中的应用.

[关键词]矩阵; 迹； 行列式； 特征值

1引言

本文中，Mm,n(C)和Mn(C)分别表示全体m×n和n阶复方阵的集合.设

A=(aij)∈Mn(C)，

(ii) 设A,B∈Mn(C)，α,β是两个复数，则tr(αA+βB)=αtr(A)+βtr(B)；

(iii) 设A∈Mm,n(C)，B∈Mn,m(C)，则tr(AB)=tr(BA)；

(iv) 设A∈Mm,n(C)，则A=O当且仅当tr(AA*)=0.

2矩阵的特征值问题

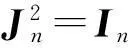
解法1注意到rankA=1，因此A至多只有一个非零特征值.因为

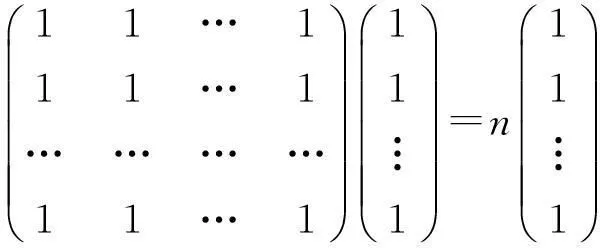
例3计算n阶矩阵

的特征值.

例4计算矩阵

的特征值.

解

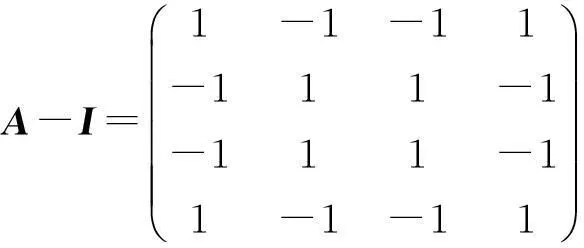
观察到其第一列与第二列和为零，第一列与第三列和为零，第一列与第四列相同，即

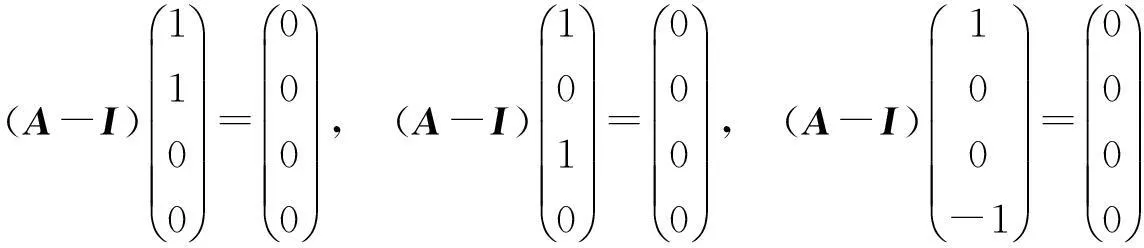
同时三个列向量(1,1,0,0)T,(1,0,1,0)T,(1,0,0,-1)T线性无关，因此0至少为A-I的三重特征值，由于tr(A-I)=4，因此A-I的特征值为0,0,0,4，从而A的特征值为1,1,1,5.

3计算行列式问题

解令

解令

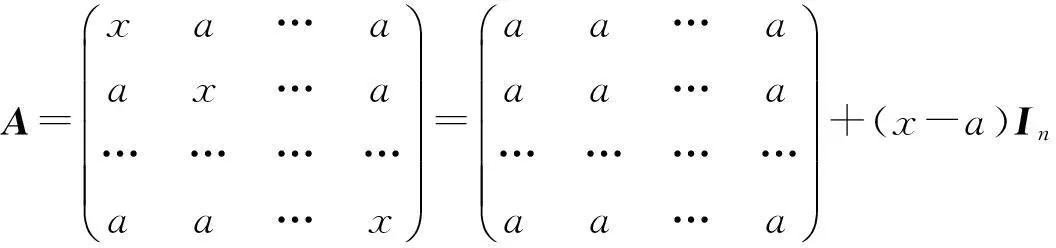
(na+(x-a))(x-a)n-1.

4矩阵性质的证明问题

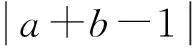
因此

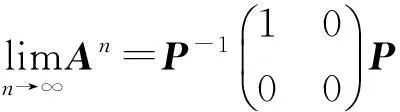
存在.

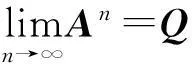
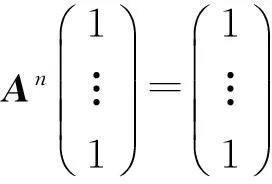
两侧令n→∞，便有

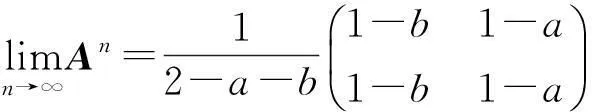
例8设A是n×n复矩阵，则A=A*的充要条件是A2=A*A(或A*2=A*A).

证必要性显然.以下证明充分性，由于A2=A*A，所以A*2=A*A，

tr(A-A*)(A-A*)*=tr(AA*-A2-A*2+A*A)

=tr(AA*-A*2)=trAA*-trA*2=trA*A-trA*2

=tr(A*A-A*2)=0.

A*2=A*A时的证明是类似的.

本文列举的8个例题，采用传统的数学方法有的是很难求解的，有的计算量是十分大的，引入矩阵迹这一工具后，问题的求解过程十分简洁.尽管大多数高等代数教材关于矩阵迹的论述并不多，但教师在授课中要重视这部分内容，要有针对性地选配一些例题供学生参考，使学生体会矩阵迹的妙用.

[参考文献]

[1]陈公宁. 矩阵理论与应用[M]. 北京：科学出版社.2007.

[2]杨字胥，高等代数习题解[M]. 济南：山东科学技术出版社，1984.

[3]盛骤，谢式千，潘承毅，概率论与数理统计 [M].3版.北京：高等教育出版社，2001.

The Application of the Trace of Matrice

JIALi-xin

(Institute of Sciences, Information Engineering University, Zhengzhou 450001, China)

Abstract:The applications of matrix trace in eigenvalue problem, computation of determinate,and the proof of matrix properties are discussed by examples.

Key words:matrice; trace; determinate; eigenvalue

[收稿日期]2013-12-09

[中图分类号]O151.21

[文献标识码]C

[文章编号]1672-1454(2015)02-0097-04