环F2+vF2上码的覆盖半径

黄德为

(合肥工业大学应用数学系，合肥230009)



环F2+vF2上码的覆盖半径

黄德为

(合肥工业大学应用数学系，合肥230009)

[摘要]通过研究环F2+vF2上线性码的结构特征，根据Gray映射，定义了两个二元码，从而证明了环F2+vF2上线性码关于李距离的覆盖半径等于两个二元码的覆盖半径之和，并得到环F2+vF2上对偶码的覆盖半径的一些结论，给出了覆盖半径的几个上下界.

[关键词]Gray映射； 笛卡尔积； 覆盖半径； 二元码； 李距离

1引言

一个码C关于汉明距离的覆盖半径是指C所在向量空间中每个向量与码C的Hamming距离的最大值.从1980年开始，研究学者们对码的覆盖半径产生了很大的兴趣.它不仅关系到数据压缩、传输，一次写入内存等实际问题，在编码理论研究中也具有十分重要的意义.覆盖半径是一个几何参数，在最小距离译码中标志着码的最大纠错能力.近年来仍有不少文章研究码的覆盖半径[1-4].在1989年，Nechaev研究发现Kerdock码可以看成环Z4上的循环码.1994年后，环Z4上纠错码理论的研究便成为纠错码理论研究的热点问题之一.几个四元素的整数剩余类环上码的覆盖半径的研究也相继出现.文献[5]研究了Z4码和其Gray映射后的二元非线性码的覆盖半径，给出了一些上下界.文献[6]研究了环F2+uF2上码的覆盖半径. 但是关于环F2+vF2上码的覆盖半径的研究很少.

环F2+vF2上码的研究一直是一个热点问题.本文约定

U=F2+vF2={0,1,v,1+v}，

其中v2=v.文献[7]讨论了环U上线性码和循环码的结构和性质，并指出了循环码与二元码之间的关系.文献[8]定义了U上码字的李重量分布的概念，给出了该环上线性码与对偶码之间各种重量分布的Mac Williams恒等式.文献[9]讨论了U上的二次剩余码.文献[10]给出了一个从U上循环码构造量子纠错码的新方法.本文定义了环U上码关于李距离的覆盖半径，利用Gray映射，定义了两个二元码，研究了U上码的覆盖半径与二元码覆盖半径的关系.

2预备知识

环U=F2+vF2={0,1,v,1+v}，其中v2=v.U也可以看成商环F2[v]/(v2+v).环U中每个元素都是幂等元，具有两个极大理想和<1+v>.U上长为n的线性码C是Un的一个U-子模. 定义U中元素0,1,v,1+v的李重量(Lee weight)分别为0，2，1，1.Un中向量x的李重量wtL(x)为其各分量的李重量的有理和.很自然的定义Un中两向量x和y的李距离dL(x,y)为x-y的李重量.C的最小李距离dL(C)定义为C中任意两个不同码字的李距离的最小值.

设x=(x1,x2,…,xn),y=(y1,y2,…,yn)为Un的两个元素，定义x和y在Un上的欧氏内积

x·y=x1·y1+x2·y2+…+xn·yn.

定义码C的对偶码

C⊥={x|x·y=0, ∀y∈C}.

如果C=C⊥，则称码C是自对偶码.

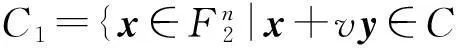
3主要结果

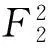
引理1.2[7]设C是U上线性码，那么有φ(C)=C1⊗C2，|C|=|C1|·|C2|而且φ(C)是线性码.

证∀(r1,r2,…,rn,q1,q2,…qn)∈φ(C),设ci=ri+v(ri+qi),i=1,2,…n.由φ是保距映射,有c=(c1,c2,…,cn)∈C.由C1,C2的定义,我们知道

(r1,r2,…,rn)∈C1,

(q1,q2,…,qn)∈C2,

因此 (r1,r2,…rn,q1,q2,…,qn)∈C1⊗C2.所以φ(C)⊆C1⊗C2.另一方面,对任意

(r1,r2,…rn,q1,q2,…,qn)∈C1⊗C2,

其中(r1,r2,…,rn)∈C1, (q1,q2,…,qn)∈C2,存在

a=(a1,a2,…,an),b=(b1,b2,…bn)∈C

使得

ai=ri+vmi,bi=qi+(1+v)ni,

其中mi,ni∈F2且1≤i≤n.因为C是线性的有

c=(1+v)a+vb=r+v(r+q)∈C.

这表明

φ(c)=(r1,r2,…,rn,q1,q2,…qn),

所以C1⊗C2∈φ(C).因此φ(C)=C1⊗C2.第二个结果易证.

引理1.3[7]设C是U上长为n线性码,C⊥是C的对偶码,则

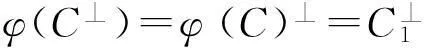
定义1.4规定Un中任一向量y与码C的李距离

dL(y,C)=min{dL(y,x)|∀x∈C}

而规定码C关于李距离的覆盖半径

RL(C)=max{dL(y,C)|∀y∈n}.

命题1.5U上码C关于李距离的覆盖半径RL(C)=R(φ(C)).

证∀x∈Un,y∈C,由引理1.1知dL(x,y)=d(φ(x),φ(y))，所以

dL(x,C)=d(φ(x),φ(C))，

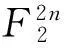
在(n,k)线性码中，二个码字x,y之间对应码元位上符号取值不同的个数，称为码字x,y之间的汉明距离，用d(x,y)表示.(n,k)线性分组码的一个码字对应于n维线性空间中的一点，码字间的距离即为空间中两对应点的距离，因此，码字间的距离满足一般距离公理，当然满足三角不等式

d(x,y)+d(y,z)≥d(x,z).

因为dL(x,y)=d(φ(x),φ(y)),所以易证对任意x,y,z∈n，一定有性质

dL(x,y)≤dL(x,z)+dL(z,y).

由这个性质可获得下面的结论.

定理1.6设C是U上码,C的最小李距离记成dL(C).C1,C2的最小汉明距离分别记成d(C1),d(C2),则

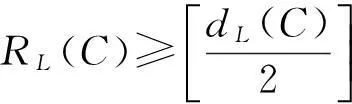
若C是线性的,则

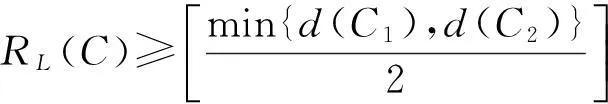
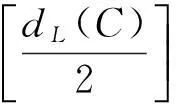
∀x,y∈C且x≠y,则

dL(x,y)≤dL(x,y+e)+dL(y+e,y).

从而

dL(x,y+e))≥dL(x,y)-dL(y+e,y)=dL(x,y)-wtL(e)

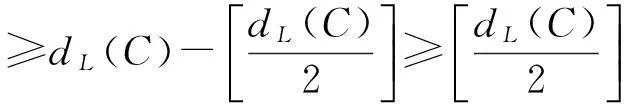
所以由定义1.4可知

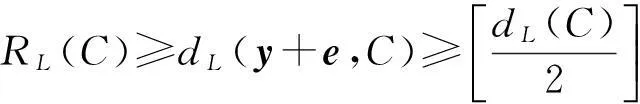
若C是线性码,由引理1.1知,dL(C)=d(φ(C)).再由引理1.2知

d(φ(C))=d(C1⊗C2)=min{d(C1),d(C2)}.

后半部分得证.

定理1.7设C是U上线性码，则

RL(C)=R(C1)+R(C2)，

而且

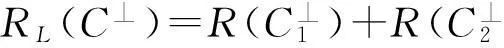
证由定义1.4及命题1.5知

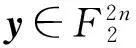
对某个y,不妨设y=y1|y2(y1,y2长度相同),再由引理2可得

d(y,φ(C))=min{d(y,x),∀x∈φ(C)}=min{d(y1,c1)+d(y2,c2),∀c1∈C1,c2∈C2}

=min{d(y1,c1),∀c1∈C1}+min{d(y2,c2),∀c2∈C2}=d(y1,C1)+d(y2,C2).

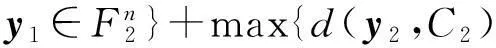
由引理1.3知

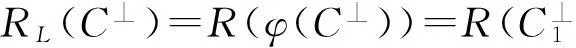
再用上面类似的证明过程可得定理后半部分结论.

引理1.4[12]记K是一个二元码(线性的或非线性的),s(K)表示K的对偶码或K的形式定义的对偶码的距离分布中不同的非零距离的数目,则R(K)≤s(K)，这个结论也称为Delsarte界.

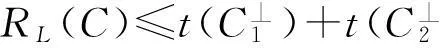
证由定理1.7知RL(C)=R(C1)+R(C2),再由Delsarte界知推论成立.

定理1.9设C是U上长为n的线性码,且C1,C2分别为[n,k1],[n,k2]线性码,则RL(C)≤2n-k1-k2.

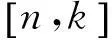
R(C1)≤n-k1,R(C2)≤n-k2.

由定理1.7知

RL(C)=R(C1)+R(C2)≤2n-k1-k2.

4结论

本文研究了环U上线性码和对偶码关于李距离的覆盖半径，给出了覆盖半径的几个上下界.这些内容的研究对进一步丰富环U上纠错码理论及构造一些性能较好的码都有一定的指导意义.也可在本文的基础上，研究一些其它有限环上码的覆盖半径.

[参考文献]

[1]Masaaki H, Michio O, Kenichiro T. On the covering radius of ternary extremal self-dual codes[J]. Designs, Codes and Crytography, 2004, 33(2): 149-158.

[2]Gerzson K, Patric R.J. O. Further results on the covering radius of small codes[J]. Discrete Mathematics, 2007, 307(26): 69-77.

[3]Gerzson K. The covering radius of extreme binary 2-surjective codes[J]. Designs, Codes and Crytography, 2008, 46(2): 191-198.

[4]姜宇鹏,邓映蒲,潘彦斌. 二维格的覆盖半径[J]. 系统科学与数学, 2012, 32(7): 908-914.

[5]Aoki T, Gaborit P, Harada M,et al. On the covering radius of Z4-codes and their lattices[J]. IEEE Trans Inform Theory, 1999,45(6): 2162-2168.

[6]李平,朱士信,余海峰. 环F2+uF2上码的覆盖半径[J]. 中国科学技术大学学报, 2008, 38(2): 145-148.

[7]Zhu Shi-xin, Wang Yu, Shi Min-jia. Some results on cyclic codes over F2+vF2[J], IEEE Trans Inform Theory, 2010, 56: 1680-1684.

[8]施敏加,朱士信,李平. 环F2+vF2上线性码的MacWilliams恒等式[J]. 计算机应用研究,2008, 25(4): 1134-1136.

[9]张涛,朱士信. 环F2+vF2上的二次剩余码[J]. 合肥工业大学学报(自然科学版),2011, 34(8): 1268-1271.

[10]Qian Jian-fa. Quantum codes from cyclic codes overF2+vF2[J]. Journal of Information and Computational Science, 2013, 10(6): 1715-1722.

[11]Dougherty S T, Gaborit P,. Harada M and Sole P. Type IV self-codes over rings[J]. IEEE Trans Inform Theory, 1999, 45(7): 2345-2360.

[12]Delsarte P. Four fundamental parameters of a code and their combinatorial significance[J]. Inform Contr, 1973,23(2): 407-438.

Covering Radius of Codes over Ring F2+vF2

HUANGDe-wei

(Dept. of Appl. Math. , Hefei University of Technology, Hefei 230009, China)

Abstract:Through the study of the structure of codes over ring F2+vF2, two binary codes was defined. By means of the Gray map, one conclusion on the covering radius of codes over ring F2+vF2for the Lee distance was obtained. We study the covering radius of dual codes over ring F2+vF2. Several upper and lower bounds on the covering radius were given.

Key words:Gray map; Cartesian product; covering radius; binary code; Lee distance

[收稿日期]2014-04-06

[中图分类号]O212.7

[文献标识码]C

[文章编号]1672-1454(2015)02-0093-04