基于SolidWorksSimulation的O型圈锥面密封非线性分析

潘广堂

【摘 要】针对工程中锥面密封存在的泄漏问题，通过两锥面之间O型密封圈进行非线性有限元分析，研究其应力分布规律，获取最大接触应力与支座反力，确定起关键作用的密封面，为锥面密封的合理设计、加工制造提供了理论依据和改进建议。

【关键词】O型圈；非线性；密封；有限元

0 前言

工程应用中经常会使用锥面密封，例如锥面密封接头、卡箍连接装置等等。由于锥面密封有结构简单、体积小、连接可靠等优点，在石油、化工等领域中得到广泛应用[1-3]。但由于制作密封圈橡胶材料的不满足胡克定律，分析锥面密封的接触应力，计算其接触反力确是工程设计的一个难题。现在我们可以借助计算机分析软件解决这一问题。

1 非线性静态分析概述

线性分析中对材料模型的重要假设：所有材料都符合虎克定律，即应力与应变成正比。有些材料只有在应变较小时才表现出这种行为。当应变增加时，应力与应变的关系变成非线性。有些材料即使当应变较小时也表现非线性行为，比如橡胶。材料模型是材料行为的数学模拟。 如果材料的应力与应变关系是线性的，该材料被称为是线性的。线性材料可以是同向性、正交各向异性或各向异性。当模型中的材料在指定载荷的作用下表现出非线性应力-应变行为时（图1），就必须使用非线性分析。非线性分析提供许多类型的材料模型。

目前处理相关工程问题主要是以连续介质力学为基础，丁晴橡胶被认为是超弹性近似不可压缩体，其力学特型表现为复杂的材料非线性和几何非线性。现阶段应用比较广泛的Mooney-Rivlin 模型，它可以用来模拟几乎所有的橡胶制品的力学行为。其函数表达式可表示为[4]

2 O型圈有限元分析

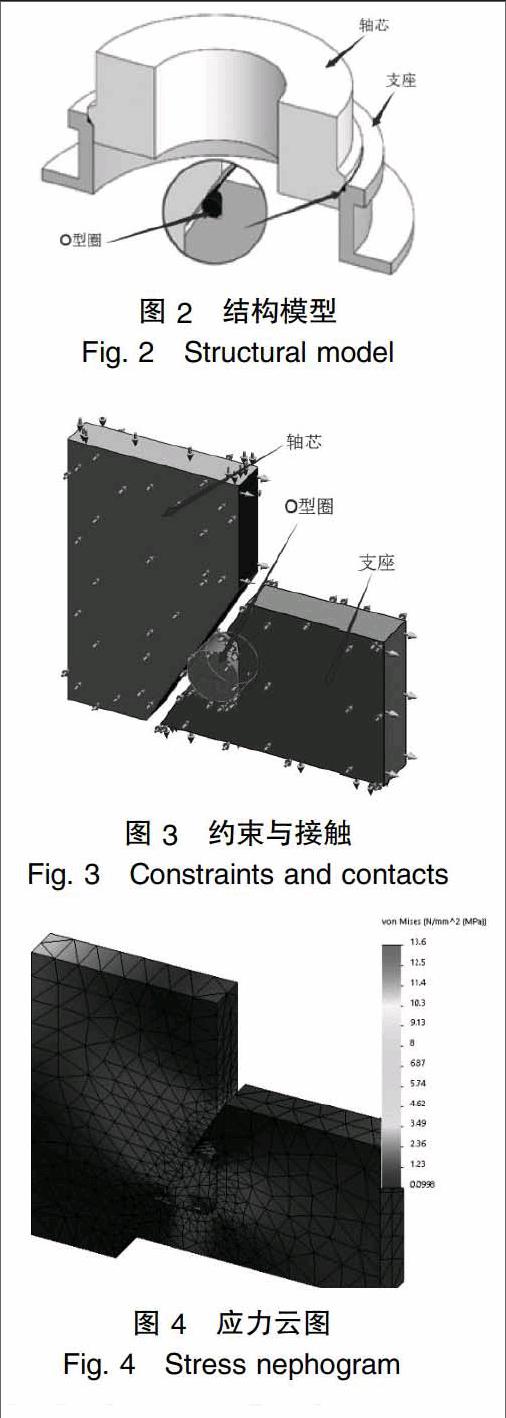
如图 2所示的结构模型中，轴芯与支座之间的密封工作由两接触锥面之间的O型圈来完成。

由于模型的轴对称性，仅对其一部分（1°角）进行分析（图 3）。O型圈被轴芯的竖直向下移动压入支座的凹槽内。轴芯和支座由35CrMo制成。

在SolidWorks Simulation中创建一个静态非线性分析，自动步进，时间增量为0.01，使用大型位移公式并选择Direct Sparse解算器，奇异性消除因子设置为0。

O型圈的材料模型设定为超弹性 Mooney Rivlin[6]，各项材料参数依据表 1。

设置模型的前、后、左、右均不可移动，支座底面固定，轴芯顶面向下移动3.4mm，如图 3。定义O型圈与轴芯、支座接触的各面接触类型为无穿透；并对各接触面使用网格精细划分，选择基于曲率的网格，最大单元大小设为1。

分析后获得应力云图如图 4所示。

分析结果的接触应力与支座反作用力如图 5、图 6所示，其最大接触应力为Cpmax=17MPa，最大反力为FN1=103N，所以支座整体反力

FN=FN1×360=37kN

O 型橡胶密封圈在工作状态下接触应力Cpmax是失效准则和失效判断的第一条件，如果Cpmax的值小于介质压力p，则会导致介质泄漏，即密封失效，所以最大接触应力应满足时效准则即保证密封条件：Cpmax≥p。由此可知该密封方案可密封17MPa介质压力。

由图 5可见，接触应力主要集中在轴芯锥面、支座凹槽底面与柱面，所以在零部件加工制造、装配时应特别注意这三个接触面的精度。

3 结论

本文介绍了非线性分析方法以及在工程中的应用的相关材料模型，并使用SolidWorks Simulation对支座与轴芯之间密封圈做非线性分析，获得最大接触应力与支座反作用力，确定了锥面密封中起主要作用的接触面，为锥面密封的合理设计、加工制造提供了理论依据和改进建议。

【参考文献】

[1]邵雅梅，周思柱，李宁.采油井口非标准卡箍设计及有限元分析[J].长江大学学报（自然科学版）理工卷，2008（01）：279-281.

[2]F. G. Lyalina V K S A. New design for a clamp connection[J].Chemical and Petroleum Engineering，1995，Vol.30（9）.

[3]史战新，甘霖.卡箍式快开对接法兰结构分析[J].舰船科学技术，2012，34（11）：75-81.

[4]杨春明，谢禹钧，韩春雨.基于Ansys的橡胶O形密封圈密封性能的有限元分析[J].石油和化工设备，2010，13（4）：21-24.

[5]任全彬，蔡体敏，王荣桥，等.橡胶“O”形密封圈结构参数和失效准则研究[J].固体火箭技术，2006（01）：9-14.

[6]李跃超.基于SOLIDWORKS Simulation的O型橡胶密封圈有限元模拟[J].智能制造，2016（2）：71-74.

[责任编辑：王伟平]