四轮独立驱动电动汽车行驶状态估计
师合迪+段敏


摘 要:在易于获得四轮独立驱动电动汽车转速和转矩的基础上,应用模糊自适应卡尔曼滤波和扩展卡尔曼滤波理论,介绍一种对车辆行驶状态进行估计的控制算法。利用非线性三自由度车辆模型采集纵向加速度、侧向加速度和横摆角速度等低成本信息,通过该算法实时地估计汽车在行驶过程中的纵向车速、侧向车速和质心侧偏角,且通过半实物联合仿真试验进行验证。硬件在环仿真实验结果表明,应用该算法能够有效地估计出车辆的纵向车速、侧向车速和质心侧偏角。
关键词:汽车行驶状态;状态参数估计;扩展自适应卡尔曼滤波;非线性
1 前言
较于传统汽车而言,四轮独立驱动电动汽车的四轮驱动力矩可以独立控制,且转矩和转速容易测得[1]。因此,在稳定性、主动安全以及节能方面,它都具有显著的控制效果。然而,四轮独立驱动电动汽车能实现整车良好控制的前提条件是其控制系统可以实时、准确地估计车辆的行驶状态参数。
卡尔曼滤波( Kalman Filter , KF)算法在线估计车辆行驶状态,是一种能有效解决上述问题的方法,但KF仅仅适用于基本的线性系统的信号估计[2]。扩展卡尔曼滤波(Extended Kalman Filter , EKF)算法是一种适用于非线性系统的无偏、最小方差估计[3]。然而,EKF算法必须要获得系统噪声和观测噪声准确的先验统计特性,否则会引起估计精度降低,终导致滤波发散。
因此,针对EKF算法的缺陷,采用一种改进的自适应EKF算法。利用该算法对汽车的纵向速度、侧向车速和质心侧偏角进行估计。实验结果表明,该算法的运算实时性较好,且估计效果也比较理想。
2 非线性汽车动力学模型
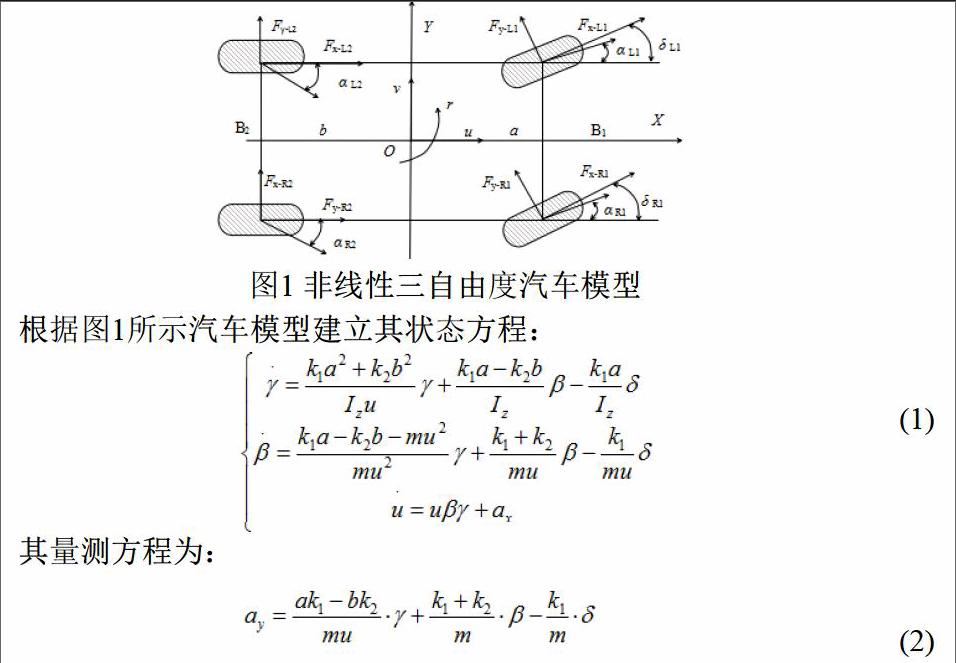
在简单的线性二自由度车辆模型[4]基础上,引入一个纵向车速自由度,就搭建成本文所采用的车辆模型,其结构如图1所示。
根据图1所示汽车模型建立其状态方程:
其量测方程为:
上式中: a、b分别为电动汽车质心到其前轴和后轴的距离,a = 1.04 m,b= 1.56 m;γ为横摆角速度,rad/ s;β为质心侧偏角,rad;u为纵向车速,m/s;前轴等效侧偏刚度k1 = - 95461 N/ rad;后轴等效侧偏刚度k2 = - 100001 N/ rad;绕z轴转动惯量Iz = 2031.4 kg.m;车辆质量m= 1182 kg;δ为前轮转角,rad;ax为纵向加速度,m/ s2;ay为侧向加速度,m/ s2 。
3 扩展自适应卡尔曼滤波
扩展自适应卡尔曼滤波(Extended Adaptive Kalman Filter , EAKF),是利用自适应卡尔曼滤波AKF滤波稳定的特点,来解决EKF由于系统参数不确定所导致的滤波发散的问题。
3.1 扩展卡尔曼滤波
EKF算法,在获取系统的状态方程、量测方程、白噪声激励以及量测误差的统计特性等信息的基础上,将非线性函数在其最佳估计点附近进行泰勒展开,且舍弃高阶分量,使非线性模型简单线性化,能够广泛地应用于各种非线性系统[5]。EKF的具体算法如下:
(1)系统的状态方程和量测方程
式中:xk为系统的状态变量;yk为量测输出;uk为控制变量;wk为系统激励噪声,vk为量测噪声,Qk 、Rk分别为其协方差。
(2)滤波器的初始化
(3)状态估计和估计误差协方差的时间更新
式中,Fk-1为状态方程f对状态变量x求偏导的雅可比矩阵,Lk-1为状态方程f对参数w求偏导的雅可比矩阵。
(4)状态估计的量测更新和估计误差协方差的更新
其中,Hk为量测方程h对状态变量x求偏导的雅可比矩阵,Mk为量测方程h对参数v求偏导的雅可比矩阵。
将该车辆模型的状态方程(1)和量测方程(2)代入上述的EKF滤波流程。其中,该系统的状态变量xk=[γ,β,u]T,量测输出变量yk=[ay],控制变量uk=[δ,ax]T。
3.2 改进滤波算法
新息[6]可认为是包含了新的信息量测的一部分,因此被用于更新状态估计。新息rk由以下方程表示
EKF是在先验估计值的基础上,利用新息rk、卡尔曼滤波增益Kk进行在线调节和修正。可将(3)中的噪声模型改写为:
其中,Q和R为初始的噪声协方差;ak和bk为在线调整权值。那么,式(5)中的状态误差协方差时间更新方程和式(6)中的滤波增益方程分别可改写为:
由于观测信息的可靠程度是渐进变化的,因此通过模糊隶属度函数将这两个置信度模糊化。将其作为模糊输入变量,同时将ak和bk作为模糊输出变量,则基于模糊逻辑对新息和噪声模型建立的卡尔曼滤波结构,如图2所示。通过新息统计特性的变化,在线监测滤波器的稳定性。当其稳定性遭到破坏时,可以选取适当的ak和bk,改变系统噪声、观测噪声的权重。这样就可以对观测信息的可信和利用程度进行调整,获得更好的性能[7]。
4 实验验证
为了更好地验证估算车辆行驶状态的扩展自适应卡尔曼滤波EAKF算法的准确性,首先应用CarSim RT与Simulink软件建立车辆动力学控制模型,如图3所示。
然后对该车辆动力学控制模型编译,将生成的实时仿真程序
载入dSPACE实时仿真系统中。利用 ControlDesk,可以根据仿真试验时需要显示的车辆仿真数据以及相应的控制按钮,在虚拟仪表库中选择相应的仪表,并建立相关的数据连接[8],如图4所示。
该实验工况设置:车速为50km/h;状态变量X0= [80/20,0,0,0,0,0,0,0,0,0, 0];路面附着系数为0.85;误差协方差矩阵P0=eye(11)*10000;采样时间间隔为0.02s;量测噪声协方差矩阵R=eye(11)*0.001;过程噪声协方差矩阵Q=eye(11)*2800。试验结果如下图5所示。
从图5可以看出,在恒定车速高附着系数路面蛇形工况下,纵向车速的估计值在趋势上基本与试验值相符合,且经比较分析其误差基本上控制在0.004以内;质心侧偏角的估计值与试验实际输出值基本一致,且经比较分析其误差基本上控制在0.02之内;横向车速的估计值跟踪CarSim软件输出的侧向车速实际值变化曲线,也有较好的跟着效果。
由此可见,基于模糊自适应的扩展卡尔曼滤波能较为准确的估算出轮毂电机电动汽车在高附着系数路面、恒定车速行驶状态下的纵向车速、侧向车速以及质心侧偏角。
5 结论
基于自适应卡尔曼滤波AKF和扩展卡尔曼滤波EKF理论,设计了一种对电动汽车行驶状态进行估计的扩展自适应卡尔曼滤波EAKF算法,能够根据方向盘转角、纵向加速度、侧向加速度和横摆角速度等参数信息实现对车辆行驶状态如纵向车速、侧向车速和质心侧偏角的准确估计。通过CarSim、Simulink和dSPACE软件联合进行半实物仿真试验,表明设计的扩展自适应卡尔曼滤波EAKF能够较为准确地估计出车辆的行驶状态参数量,也说明了其具有较好的适应性和鲁棒性。
参考文献
[1] 宗新怡,李刚,邓伟文.四轮独立驱动电动汽车车速估计研究[J].机械设计与制造,2013,(9):83.
[2] 宋文尧,张牙.卡尔曼滤波[M].北京:科学出版社, 1991:57-59.
[3] Simon Haykin.自适应滤波器原理(第4版)[M].北京: 电子工业出版社,2003:91-93.
[4] 余志生.汽车理论(第3版)[M].北京:机械工业出版社,2004:116-118.
[5] Welch G ,Bishop G. An introduction to the Kalman Filter[M]. Chapel Hill: University of North Carolina Press, 2006: 28-29.
[6] Dan Simon. Optimal state estimation kalman —H∞ and nonlinear approaches[M]. Beijing: National Defense Industry Press, 2013:121-123.
[7] Greg Welch ,Gary Bishop. Introduction to Kalman filter[J]. Department of Computer Science, University of North Carolina at Chapel Hill3,Chapel Hill, NC 27599-3175.
作者简介:师合迪,男,汉族,就读于辽宁工业大学汽车与交通工程学院 电动汽车关键技术。

