无穷多个无穷小量乘积的探讨

马锦娟,　郑　挺,　姚晓鹏

(浙江工商大学统计与数学学院，浙江杭州310018)



无穷多个无穷小量乘积的探讨

马锦娟,郑挺,姚晓鹏

(浙江工商大学统计与数学学院，浙江杭州310018)

[摘要]文献[1,2,3]举出反例来证明无穷多项无穷小的乘积不一定是无穷小.本文主要是对这三个反例合理性的置疑.

[关键词]数列； 无穷小量； 积

1引言

一般教科书中均介绍了结论：无穷多个无穷小的乘积不一定是无穷小.为了说明这个结论的正确性,文献[1,2,3]都举出了反例,我们对这些反例中乘积的因子是否都是无穷小量提出置疑.

下面对文献[1,2,3]中给出的反例提出一些看法.

2例子

2.1　文献[1]中给出例子

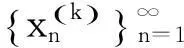
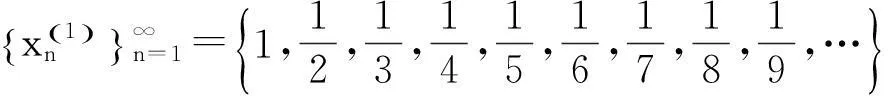
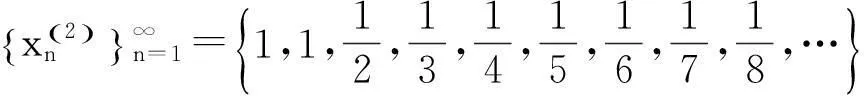
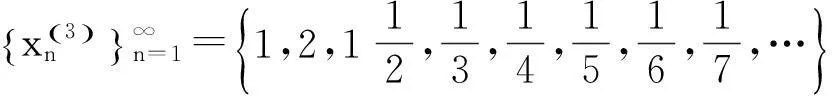
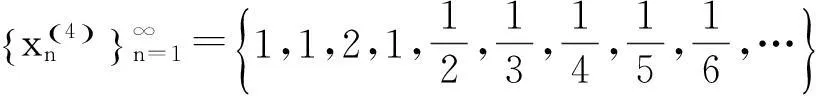
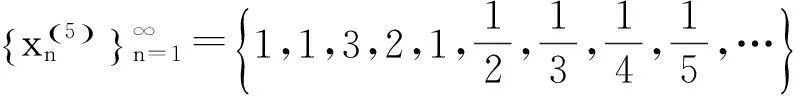
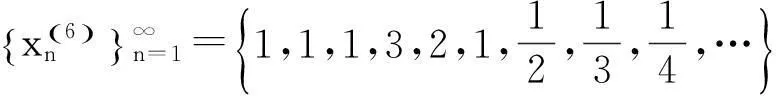
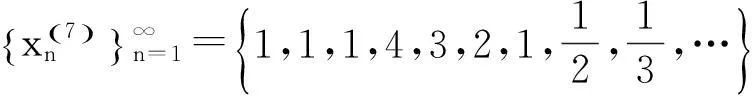
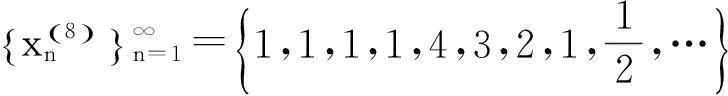
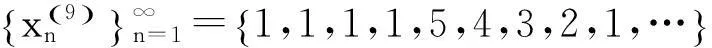
2.2　文献[2]中给出例子

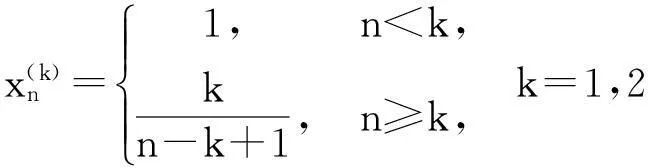
该例给出了如下无穷多个数列：

……………………………………

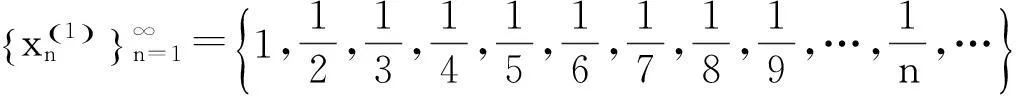
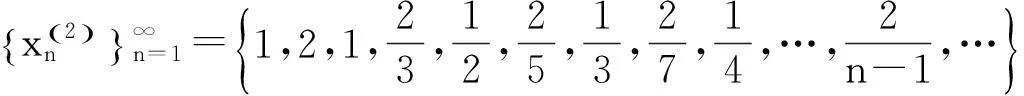
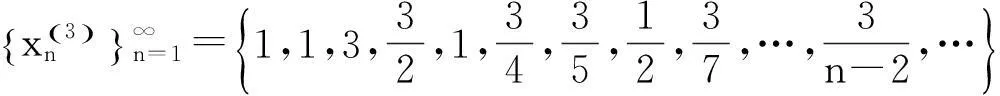
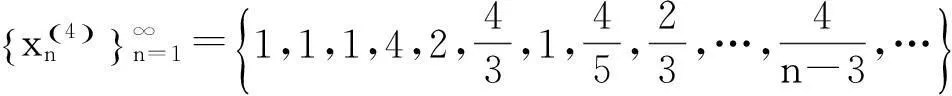
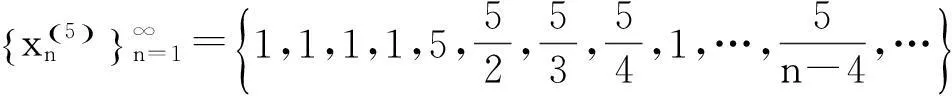
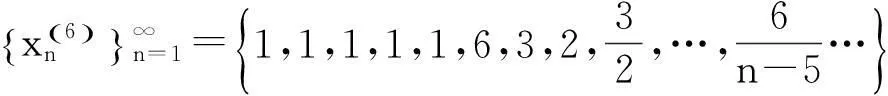
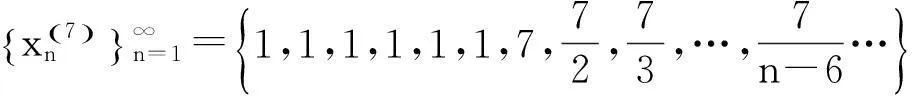
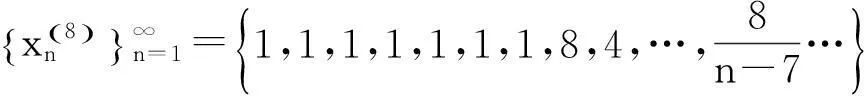
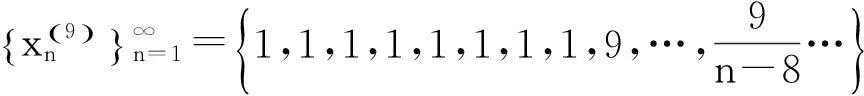
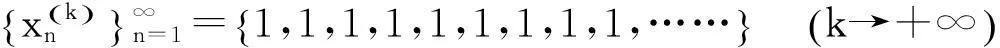
既然所构造的数列不能满足每个因子都是无穷小量，所以所得结论“无限个无穷小量的积不一定是无穷小量”不可信.

2.3　文献[3]所举例子

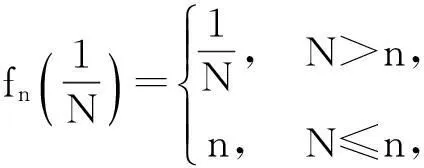
该例给出了如下无穷多个数列：

…………………………………………

…………………………………………

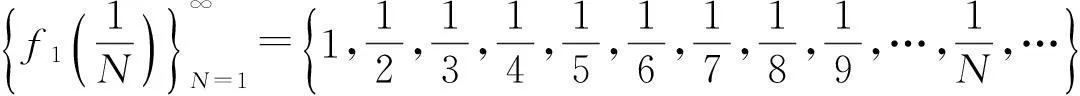
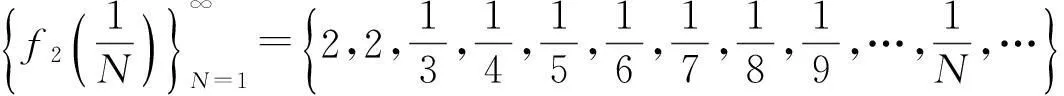
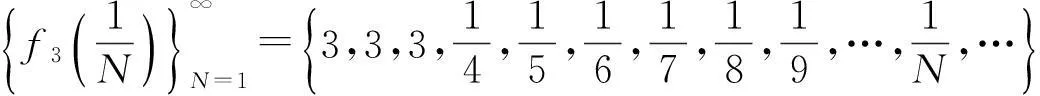
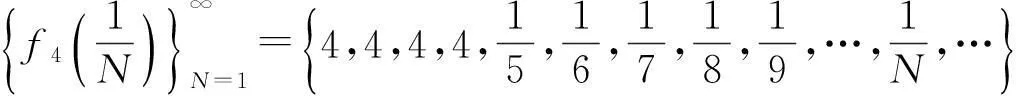
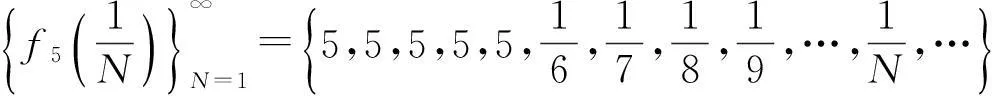
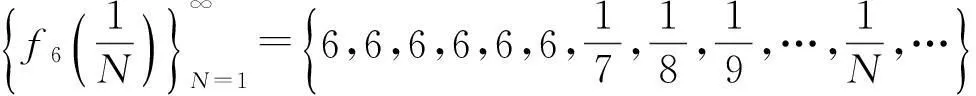
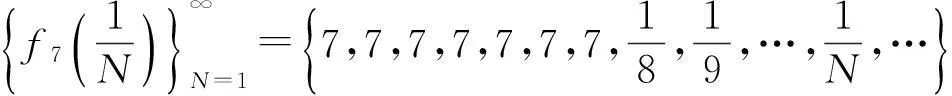
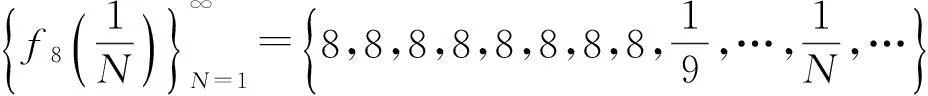
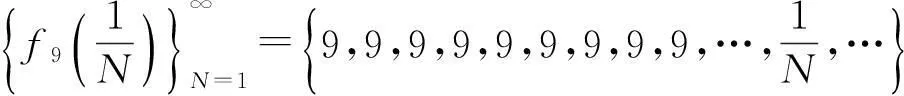
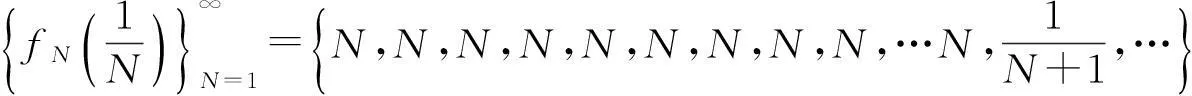
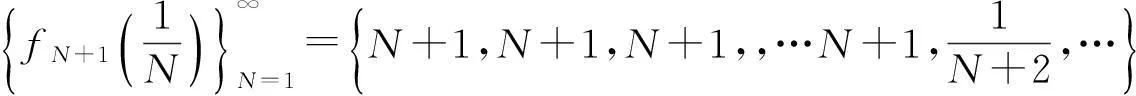
2.4　其　他

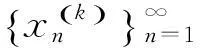
3结论

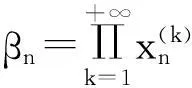
[参考文献]

[1]严莉萍,焦振华.关于高等数学中几个易错命题的举例说明[J]. 大学数学, 2012,28(2):131-134.

[2]戎海武,王向东.关于无穷大和无穷小的几个问题[J]. 高等数学研究, 2007,10(5):3-5.

[3]孟健,赵迁贵.关于无穷小量乘积的讨论[J]. 数学的实践与认识,2002,32(3):517-519.

[4]刘红卫,于力.关于无穷多个无穷小的乘积的注记[J].高等数学研究,2002,5(3):27-28.

Annotations on the Product of Infinite Infinitesimals

MAJin-juan,ZHENGTing,YAOXiao-peng

(Mathematics and Statistics Faculty of Zhejiang Gong Shang University, Hangzhou Zhejiang 310018,China)

Abstract:Document[1，2，3] set counterexamples to prove the product of infinite infinitesimals not necessarily to be infinitesimal. This article primarily questions the reasonability of the three counterexamples.

Key words:series; infinitesimal; product

[基金项目]浙江省自然科学基金项目(Y1111039)

[收稿日期]2014-01-15

[中图分类号]O171

[文献标识码]C

[文章编号]1672-1454(2015)01-0067-03