经历过程 提升学生思维能力

孙宇

【关键词】思维能力 小学数学 创设情境 动手操作 联系实际

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2015）10A-0115-01

在小學数学教学中，新课标将思维能力的发展列为核心能力培养，但在实际教学中，并没有切实按照这一目标来落实，教师往往只注重对概念、公式的运用和记忆，而忽视学生思维能力的培养，导致学生高分低能。究其原因，主要在于教师在课堂上没有给学生提供足够的探究空间，学生不能有效经历概念的形成过程，思维受到限制，因此也就没法发挥主体作用。如何培养小学生的数学思维能力呢？笔者谈三点思考和体会。

一、创设情境，引发自主猜想

新课标明确指出，教师要发挥学生的主体性，让学生经历观察、操作、分析等过程，获得思维能力的提升。小学生的思维大多还停留在直观形象的水平层面，因而在学习抽象的数学概念时，对数学本质的理解存在一定的难度。有基于此，教师要紧扣教材，结合教材内容为学生提供丰富的素材，设计有效的数学活动，将新旧知识有机衔接，引发学生的猜想，让数学探究充满思维含量。

例如，在教学苏教版五年级数学上册《小数乘小数》时，笔者出示生活情境，让学生思考：客厅长为3.6米，宽为4.8米，客厅面积是多少平方米？学生先运用估算算出客厅的面积大致为20平方米。笔者引导猜想：如何算出准确的面积？用你的方法试一试。学生分组讨论后认为，可以将长和宽换算成分米，即36×48=1728（平方分米），再换算成平方米即可，也就是17.28（平方米）；另一组认为，可以用整数乘整数的方式进行计算。此时笔者追问：积的小数点该如何点？学生展开讨论，认为两个因数相乘，其中一个扩大10倍，另一个也扩大10倍，那么积就扩大了100倍，因而积要再缩小100倍。也有学生猜想认为，小数乘小数的积的小数位应当是两个因数的小数数位之和。笔者让学生进行验证，学生自己出题展开探究，对计算结果进行讨论。在学生讨论结束后，笔者启发学生：你发现了什么规律？小数乘小数的计算法则是什么？学生通过猜测和验证，对小数乘小数的计算法则有了初步感知，对计算规律也有了自己的理解，从而获得对算理的深刻感悟。

二、动手操作，加强感性积累

在小学数学教学中，学生的抽象思维发展需要一个过程，教师要提供充足的空间和时间，加强感性积累，让学生参与实践，将操作和思维有机结合，经历数学思维过程，从个例中发现规律，展开合情推理，进行归纳演绎，发展思维能力。

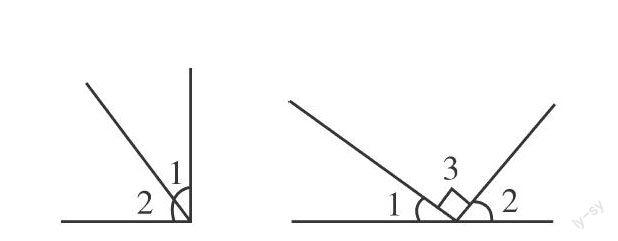
例如，在苏教版教材中有这样一道综合题：判定“在一个三角形中，如果∠1+∠2=∠3，这个三角形一定是直角”。显然，要让学生做出正确的判断，就要让他们有足够的知识积累和储备。为此，笔者让学生先从复习旧知入手进行思考：三角形的内角和是多少？学生认为，三角形的内角和为180度。此时笔者从特殊的直角三角形入手，追问：如何验证三角形内角和是180度？学生动手操作，采用量一量、拼一拼的方法，认为可以将两个锐角叠放在直角上，这样就是两个直角，加起来就是180度；也有学生认为，可以将三个角折起来，拼成一个平角（如下图）。

根据这一操作，学生对∠1+∠2=∠3有了直观认知，并能进行合情推理，得出正确判断。显然，学生的推理是从最初的感性开始的，教师引导操作，使学生的感性知识和经验不断增强，并逐渐上升为理性经验，进而发展了学生的数学思维。

三、联系实际，推进生活实践

在新课改背景下，小学数学教材中新增了实践运用环节，这是培养学生实践能力的一个重要组成部分。教师在教学中要借助生活实践，带领学生根据生活实际解决数学问题，建构推理意识，提升数学思维。

例如，在教学苏教版六年级数学下册《比例》时，笔者根据教材内容设置了一道实践运用题：学校有一棵大树，现在要测量它的高度，你怎么做？学生提出了测量办法：有的认为可以爬到树上系一根绳子放下来，然后测量绳子的长度即可。这个方法立刻遭到了其他同学的一致反对。有的认为将大树放倒来测量，这个提法也立刻被否定了。笔者引导学生思考：能否运用比例来进行计算呢？想一想用什么办法？学生根据比例的性质，发现可以采用影子和大树的比例来进行测量。学生将一根木棒固定在大树旁边，测量出大树的影长，木棒的影长，还有木棒的长度，而后利用同一时间内大树和影长高度的固定比例，计算出大树的高度。

这样，通过联系生活实际，抓住比例与生活的关联，帮助学生巩固所学知识，并通过已学知识展开思维，在解决问题中建构解决问题的意识。

（责编 林 剑）