为复习课插上探究的翅膀

【关键词】高中数学;复习课;教学设计

【中图分类号】G633.6 【文献标志码】A 【文章编号】1005-6009（2015）42-0053-02

【作者简介】吴洪生，江苏省清浦中学（江苏淮安，223002）副校长，中学高级教师，淮安市数学学科带头人。

【设计说明】

1.直线与方程是高中解析几何的入门知识，用方程表示直线，将几何问题代数化。在平面解析几何教学中，要帮助学生不断地体会“数形结合”的思想。在教学中应注意“数”与“形”的结合，在通过代数方法研究几何对象的位置关系以后，还可以画出其图形，验证代数结果;同时，通过观察几何图形得到的数学结论，可对结论进行代数证明，而不是割断它们之间的联系，只强调“形”到“数”的方面，而忽视“数”到“形”的方面。

2.复习课不同于练习课，一节课，若学生练得太多，教师固然轻松，但由于学生无法形成知识系统，学生会觉得这样复习乱而无益，收获不大;若教师讲得太多，重视技巧，忽略基础，师生双方都会疲惫不堪。这样势必造成学生对复习课感到厌烦，不但没有起到“温故知新”的效果，还削弱了学生对数学学习的兴趣与劲头。于是笔者考虑在学生对直线方程已经学习过的基础上，只需让学生自主复习解题，由学生自己发现细节或易错问题，教师及时适当提醒与点拨。同时笔者在深度和广度上下功夫，教学中比传统的复习课增加了运用直线方程解决相关最值问题，通过猜想、尝试、分组讨论、反思等过程，使复习课也插上探究的翅膀，把不同章节知识、不同的解题方法有机地联系在一起，让学生不再受传统解题方法的束缚，思维更加开阔。

【教学设计】

一、教学目标

1.了解两个独立条件确定一条直线;

2.熟练运用点斜式、截距式、两点式求直线方程;

3.运用直线方程解决有关最值问题。

二、教学重点

1.求解直线方程。

2.运用直线方程解决有关最值问题。

【教学过程】

一、课前自主导学

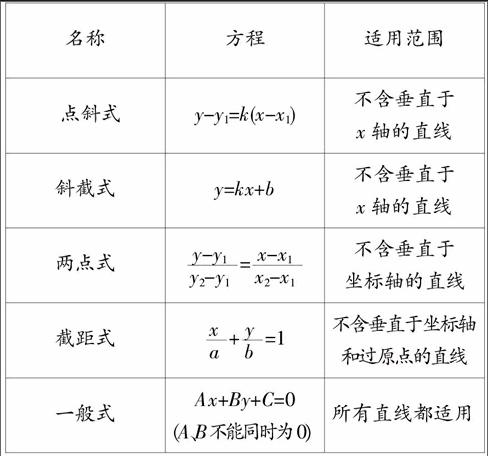
首先由学生口答直线方程的五种形式：

接着用下列三道习题来巩固学生的基础知识点。

（1）过点P（-2，5），且斜率为1的直线方程为

。

（2）过两点（0，3），（2，1）的直线方程为   。

（3）过点（-4，2），在y轴上截距为-2的直线方程为             .

设计意图：复习回顾本章学习的主要内容以及重要的数学思想方法，让学生迅速进入学习状态，通过对情境例题的逐步分析和探究，引导学生自觉形成系统的知识结构，梳理全章知识，加深复习印象。

二、经典题型演练

题型一 求直线方程

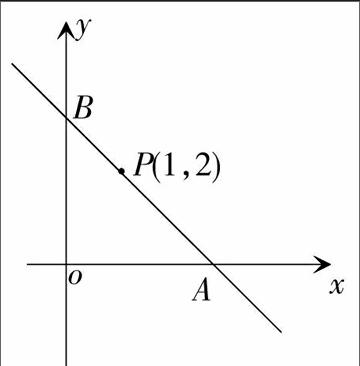
例1.如图，求过点P（1，2）且满足下列条件的直线方程。

（1）倾斜角是直线l1：3x-y+10=0的倾斜角的2倍;（2）在两坐标轴上截距相等;（3）点A（-1，-2）到该直线的距离等于2。

设计意图：本题侧重于考查学生对基础知识的掌握，但本例绝不“简单”。它至少有两个易错点：①与截距有关的直线方程求解时不能忽视截距可能为零的情形;②求直线方程时，若不能断定直线斜率是否存在时，应对斜率是否存在加以讨论。此外，本例的第二问还可以做如下拓展：若条件为直线在两坐标轴上的截距绝对值相等，结果是什么？若条件为直线在x轴上的截距是在y轴上的截距的2倍，结果又是什么？

从学生自主探究的教学原则出发，在具体的教学过程中宜先由学生自主做题、体会本题的易错处，再由教师适时点拨、提醒，从而达到良好的教学效果。

题型二：与直线方程有关的最值问题

例2.如上图，过点P（1，2）的直线与x轴的正半轴、y轴的正半轴分别交于A，B两点，求：（1）△AOB的面积的最小值;（2）OA+OB的最小值;

（3）PA·PB的最小值。

设计意图：本例属于综合性问题，有一定的难度。本例的经典性体现在如下几个方面：首先，本例的三个问题都可采用点斜式方程来求解，虽然此法在某些步骤上稍显笨拙，但只要一步一步仔细求解，最终也能得出结果;其次，本例的三个问题也可采用截距式方程来求解，而且在涉及面积问题时，截距式方程更为直观;再次，无论选用哪种方程，本例都要用到“基本不等式”这一工具，在一定程度上顺便对不等式的相关知识做了复习;最后，在实际的教学过程中发现，学生在经历讨论、思维碰撞后能提出许多有新意的解法，例如，在求解第一个问题时，有学生在选用截距式后利用a，b关系实施消元把面积表示为关于b的函数，进一步令b-2=t（t>0），将面积表示为关于t的函数，体现了数学解题中的消元思想、换元思想;还有学生在求解时，令=sin2α，=cos2α，利用三角函数中的平方关系来构造基本不等式，利用跨章节的知识来解决问题。这也从一个侧面反映了以学生自主探究进行复习课教学的魅力。

在教学中应当先让学生进行小组讨论，充分调动小组合作的力量，引导学生拓宽思路，找寻不同的解法，力求让处于不同层次水平的学生都有所收获。

三、全课总结

求直线方程的方法最常用的为两种，一是直接法，二是待定系数法。这两种方法在本节课的两个例题中均有所体现。此外，在本节内容中，我们也用到了数形结合、分类讨论以及方程等数学思想。

在涉及直线方程的问题中尤其需要注意：一、与截距有关的直线方程求解时不能忽视截距可能为零的情形;二、求直线方程时，若不能断定直线是否具有斜率，应对斜率是否存在加以讨论。

【设计反思】

教学设计要考虑学情，学生的真实状态是课堂教学活动的出发点。新课程理念下的课堂教学设计不仅要体现学生的自主性和活动性，同时要体现数学问题的情境性和可接受性，要注重学生的探究与合作。通过前面内容的学习，学生已经对解析几何这一内容有了基本的了解，知道了解析几何是用代数方法研究几何问题。本节内容，由于学生基础较好，学习积极性较高，思维活跃，所以教学中大胆放手给学生，让学生大胆探究，突出一题多解，开发学生思维，让学生始终是课堂的主人。