小改变大不同

余亚明

[摘 要] 变式教学对提高学生的学习积极性，拓宽学生的思维空间，提高教育教学水平有一定的帮助，本文从三个方面举例说明“变式教学”的优势：变式教学帮助学生理解新知；变式教学利于学生解决问题；变式教学促进学生学会变通.

[关键词] 变式教学；方法；优势

变式教学就是对数学中的例、习题进行不同背景、不同情形、不同角度、不同层次的变式，从而暴露问题的本质，揭示相关知识间内在联系的一种教学方法. 通过变式教学，可使学生触类旁通，达到一题多用、一法多用、多题一解、多题归一的效果，从而提高学生的学习积极性，拓宽学生的思维空间，提高教育教学水平，下面结合课堂教学实践从三个方面举例说明“变式教学”的优势.

变式教学帮助学生理解新知

学生在刚接触一个新的数学概念时，很容易只停留在知识的表层，通常难以理解概念的内涵和外延. 所以在新概念形成过程中要多方面呈现概念的外延并接触一些“貌合神离”的情形，以便突出概念的内涵，这样能帮助学生正确、深刻地理解新知并掌握新知.

例1 学习一次函数时，在学生了解了“形如y=kx+b（k、b是常数，k≠0）的函数是一次函数”的概念并让学生对几个简单的函数解析式进行辨别后，可以设计这样的变式训练：

学生在解决变式4和变式5时出错率很高，他们把（m2-4）xm错误理解成最高次项，这时教师在学生出错的基础上适当点拨，（m2-4）xm的次数可以高于一次，得出m2-4=0；（m2-4）xm的次数可以是一次，得出m=1；（m2-4）xm的次数也可以是零次，得出m=0. 变式4共有三种答案，变式5在变式4的基础上要考虑系数m-2.学生听完讲解恍然大悟，理解了自己出错的真正原因，加深了对概念的理解，这样由表及里，由浅入深，层层深入，环环紧扣，给学生清晰的层次感，从层层递进的变式中激活学生的思维，同时使学生的思维有了深度和广度，更让学生学会了知识的迁移.

变式教学利于学生解决问题

很多学生在解题时，一旦遇上把题目条件或图形结构做少许改变的题目，就会感到无从下手. 其实这些变了的题目与原题在知识、方法上是有关联的，只要引导学生对这些题目进行类比，归纳解决它们的常见方法及数学思想，就能达到解一题、融一类、会一片的境地，从而提高学生的解题能力.

在平行四边形的判定定理3的教学时，可以这样设置一组变式题目：

例2 如图1，？荀ABCD的对角线AC，BD相交于点O，E，F是AC上的两点，并且AE=CF，求证：四边形BFDE是平行四边形. （新人教版数学八年级下册教科书46页例3）

教科书主要是利用“对角线互相平分的四边形是平行四边形”这个判定定理来证明四边形BFDE是平行四边形.

变式1 如图2所示，若将例题中的已知条件E，F是AC上的两点，改为点E，F在AC两侧的延长线上，其他条件不变，四边形BFDE是平行四边形吗？为什么？

虽然点E，F位置改变但引导学生抓住实质，利用等式性质仍能证出OB=OD，OE=OF，还可以利用例题的判定方法.

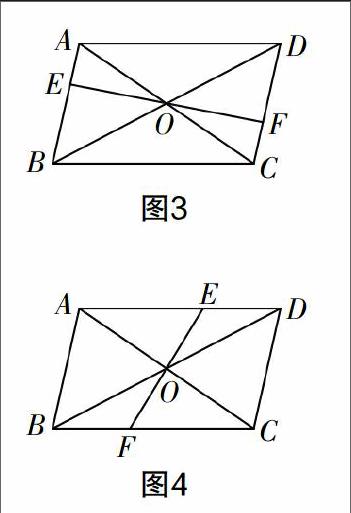
变式2 如图3、4所示，？荀ABCD的对角线AC，BD相交于点O，直线EF经过点O与？荀ABCD的对边分别交于点E，F，四边形BFDE还是平行四边形吗？为什么？

这时，点E，F的位置到了平行四边形的边上，有了前两题作为铺垫，不管是图3还是图4，学生很容易联想到证OB=OD，OE=OF，从而证到结论. 加深了学生对判定定理的理解，又培养了学生思维的发散性.

变式3 如图5、6，？荀ABCD的对角线AC，BD相交于点O，直线EF经过点O与？荀ABCD的对边所在的直线分别交于点E，F，四边形BFDE还是平行四边形吗？为什么？

变式3在变式2的基础上进一步加深，由点E，F的位置在线段上变为在直线上，范围扩大，教学时可以在前面图形的基础上让学生自己画出满足条件的图形加以探究，发现此问题仍然可以利用例题的判定方法得出相同的结论. 通过变式3的训练可以加深对判定的灵活应用，充分培养学生的解决问题的能力和探究能力.

变式教学促进学生学会变通

教学中经常遇到这样的情形：学生对所学知识点掌握较好，也形成了一定的解题经验，但容易产生思维定式，一旦遇到变通就束手无策. 因此，教学中不能墨守成规，要注重对比分析，渗透变通意识.

例3 如图7，菱形ABCD的对角线长分别为6和8，点M，N分别是边AB，BC的中点，点P是对角线AC上的一个动点，求PM+PN的最小值.

这是一道典型的动点最值问题，其特征是一动两定型，即一个动点（点P），两个定点（点M，N）. 采用对称共线法，利用轴对称变换，如图8，将线路中线段PM，PN映射到同一直线上（线路长度不变），从而确定动点P的位置，并计算线路最短长度，也就是MN′的长度5.

变式 如图7，菱形ABCD的对角线长分别为6和8，N是边BC的中点，点M、点P分别是边AB、对角线AC上的一个动点，求PM+PN的最小值.

变式中，M点已经变为动点，其特征是两动一定型，即两个动点（点M，P），一个定点（点N），所以P点的确定与例题大不相同，这时引导学生思考：

（1）M点还一定是AB的中点吗？

（2）线段PM，PN如何映射到同一直线上？

（3）如何让线路长度最短？

通过思考，启发学生对比联系变式与例题之间的联系和区别，学生能顺利地利用轴对称变换及“垂线段最短”的知识确定出动点P的位置，如图9，计算出线路的最短长度，也就是MN′（菱形的高）的长度4.8.

例4 如图10，在？荀ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF，CF，则下列结论中一定成立的是______. （把所有正确结论的序号都填在横线上）

变式 如图12，教师可从以下角度对学生进行点拨，取BC的中点G，连接FG，交EC于点H，可得四边形FGCD是菱形，则①轻松得出；再连接EG，易得GE=GC，又GH⊥EC，故FH垂直平分EC，则②④就能随之得出了；因为S△BEC=2S△CEG，而S△CEF 不一定等于S△CEG，故③不成立.

变则通，通则灵，灵则活，这样的变式训练开阔了学生的解题思路，能使学生从单一的思维模式中解放出来，有利于将知识、能力和思想方法用于更多的新情景、更高的层次中，通过不断地反复渗透，从而达到对知识螺旋式的再认识，再深化，乃至升华的效果.

以上是笔者在教学实践中的一点尝试，当然，变式教学中的变式训练不是为了“变式”而变式，而是要根据学生的学情，遵循学生的认知规律而设计，其目的是通过变式训练，使学生在理解知识的基础上，把学到的知识转化为能力，形成技能和技巧，完成“应用—理解—形成技能—培养能力”的认知过程. 因此，教学中数学变式训练设计要巧，要有一定的艺术性，要正确把握变式的度，要有目的性，要起到引导、激发学生思维活动的作用.

总之，数学教学中变式教学是对学生进行数学技能和思维训练的重要方式，它能有效地培养学生思维的深刻性、开阔性、发散性、灵活性和独创性. 因此，在数学教学中我们要善于利用变式教学，激活学生思维，提高课堂教学的有效性.endprint