常微分方程在数学建模中的有效运用研究

王复友

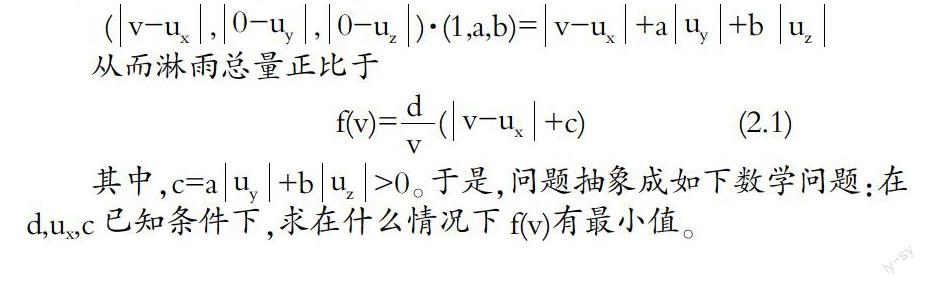
【摘要】常微分方程是17世纪随着微积分发展起来的一种研究连续量变化的工具和解决很多实际问题与数学直接的桥梁的应用学科。牛顿证实地球公转的轨道是椭圆形的就是通过对常微分方程进行求解得出的。海王星的发现也是科学家在解开常微分方程得出的结论，事实上确实是通过这样发现了海王星的存在。

【关键词】常微分方程 数学建模 数学模型

【中图分类号】G42 【文献标识码】A 【文章编号】2095-3089（2015）04-0171-01

一、数学模型的概念

所谓的数学模型就是通过对数学工具的运用从而把实际问题和理论知识相结合，并且解释具体的现象和情况对未来的事物发展方向进行预测，从而进行控制优化，以便更好的指导社会生活发展等。数学建模的基本流程就是：实际问题建模构建数学模型；然后对数学模型运用数学工具进行数学处理；得到处理后的数学模型的解；通过对数学模型的解加以阐述和解释来得出实际问题的解；最后通过实际问题的解回归到实际问题中加以预测或者解决问题。所以，数学模型其实就是通过数学工具或者数学语言对实际问题的一个概况描述。主要目的就是为了解决实际问题。

二、数学建模的方法

第一步准备模型，首先是对想要建模的实际问题进行了解，确定建模目的，弄清建模的内容方向，然后通过计算机或者在图书馆查阅相关信息，然后对问题进行总结分析，进行深入研究调查。

第二步是通过对模型的深入调查研究以后，对问题进行化繁为简，抓住问题的主要因素，把次要的不影响大的结果的因素忽略简化，进而对模型提出假设构想，然后不断的进行修改和完善。

第三步是在模型假设的基础上，选择正确的合理的科学的数学工具对实际问题的变量进行描述，要注意分清变量的类型，正确选择合适的数学工具建立微分方程。要尽可能的把握问题的本质，简化掉多余的信息，进行严密周祥的推理，同时要保证思路清晰、明了尽量提高准确性，科学性。

第四步是在上面的基础上，运用对微分方程的求解来解释具体问题。

第五步是在得到模型的解以后，对它进行分析检验，然后与实际情况结合比较，如果结果误差小，说明模型是成功的，反之要对模型进行修改再重复上面的步骤，一直到正确的模型得到正确的解。

最后是把上面得到的模型的解，运用到实际问题中，进行预测分析。一般情况下，建模可以对事物发展进行预测，而预测可以为决策者决策控制提供有效的信息。

四、常微分方程在数学建模中的运用

上文已经对数学建模的过程进行了简单概述，以及模型的分类。现在以实际实例来说明常微分方程在数学建模中的实际应用。

人们日常生活中外出时难免碰到下雨却没有带伞的情况，怎么样才能少淋雨是一个问题。我们就怎么减少淋雨程度进行研究。

模型假设：通过描述可以知道主要因素有：雨的大小，方向以及人走路的路程和速度。为了建立模型我们提出这样的假设：1把人当做长方体，顶，侧、前的面积比是b：a：1；雨中某地直线距离d，风速和雨速都不变，建立一个直角坐标系（V，0，0），设雨速（ux，uy，uz）：

在上述假设下，由高等数学中曲面积分的通量概念，显然，单位时间内的淋雨量正比于

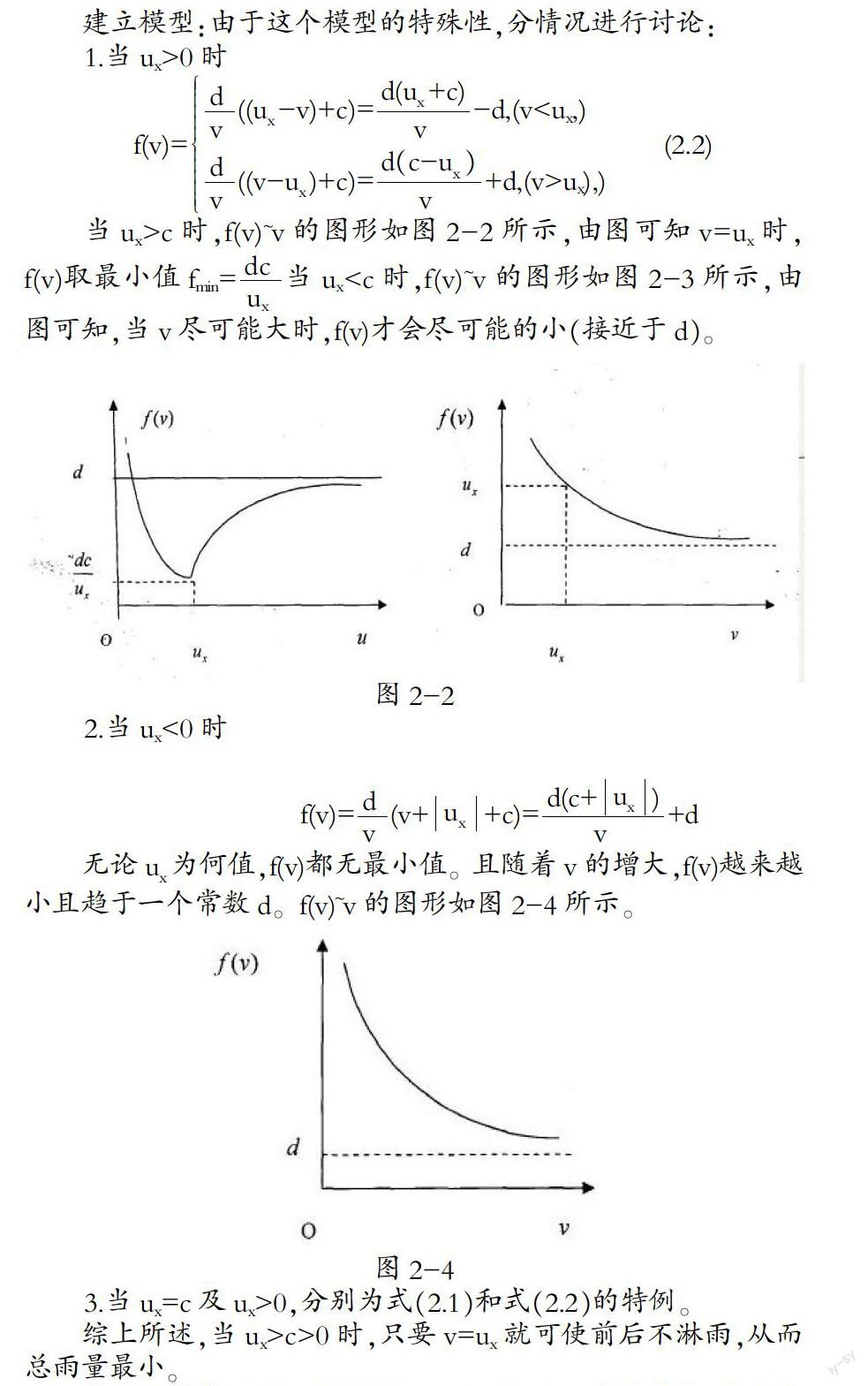
3.当ux=c及ux>0，分別为式（2.1）和式（2.2）的特例。

综上所述，当ux>c>0时，只要v=ux就可使前后不淋雨，从而总雨量最小。

除此之外都应尽可能的使v最大，所以只有跑得快，才会淋雨少。

五、结束语

综上所述，常微分方程在数学建模的运用是一个长期细致系统性的工程，通过教学实践发现常微分方程在数学建模中的运用可以大大提高学生的学习积极性和对数学知识的运用。在今后的教学中，应该在现有的基础上继续对数学建模和常微分的结合使用进行深入探究，更好的引入常微分方程在数学建模中的运用，以便提高教学质量。

参考文献：

[1]韦程东，高扬，陈志强等.在常微分方程教学中融入数学建模思想的探索与实践[J].数学的实践与认识，2008，38（20）：228-233.