弹性模量对柔性仿生鱼尾振动行为的影响*

官源林， 李华峰， 杨熙鑫， 狄思思

(1.南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016)(2.青岛大学软件技术学院 青岛，266100)



弹性模量对柔性仿生鱼尾振动行为的影响*

官源林1， 李华峰1， 杨熙鑫2， 狄思思1

(1.南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016)(2.青岛大学软件技术学院 青岛，266100)

针对采用各向同性材料为基板的仿生鱼尾刚度大、变形小的情况，研究基板材料弹性模量对于柔性复合型仿生鱼尾振动行为的影响。首先，通过使用粗压电纤维复合材料(macro fiber composite，简称MFC)作为驱动器，设计了一种柔性仿生鱼尾结构，运用COMSOL Multiphysics有限元软件模拟了具有相同泊松比和密度的基体材料在不同弹性模量下的鱼尾振动情况，得出鱼尾摆动位移与弹性模量间的极值关系；然后，对比此种弹性模量下各向同性材料与各向异性材料，得到各向异性材料适合作为基体材料的结论；最后，根据仿真结果制备出各向异性基体材料，与MFC相结合得到柔性鱼尾，再对其进行振动性能测试实验。实验结果验证了数学模型的合理性及设计的可行性。

粗压电纤维复合材料； 玻璃纤维复合材料； 弹性模量； COMSOL有限元软件

引言

鱼类推进模式的研究是新型仿生鱼水下推进器的研究基础。Breder首先依据鱼类推进模式不同对其进行分类[1]，分为身体/尾鳍模式(body and/or caudal fin, 简称BCF)和中央鳍/对鳍模式(median and/or paired Fin, 简称MPF)。BCF模式是借助身体波动运动或尾鳍摆动运动产生推进力，MPF模式主要借助尾鳍以外的运动产生推进力[2-3]。BCF模式能够产生大推力并具有高速巡游和快速启动的能力[4-5]，因而受到研究者的广泛关注。

随着智能材料的不断涌现，具有小型化、机动性强、隐蔽性好和噪声污染小等特点的仿生鱼已成为一个热门研究对象。镍钛形状记忆合金驱动[6-7]、超磁致伸缩薄膜[8-9]、人工肌肉(ion-exchange polymer metal composite，简称IPMC)[10-11]等材料已应用于此领域。考虑到这些材料的自身缺陷，研究者开始了对复合材料的探索。粗压电纤维复合材料(macro fiber composite，简称MFC)在1996年首先被NASA发明，2002年其作为专利发明在世界范围内被广泛应用。它把若干根矩形压电陶瓷(PZT5A)棒嵌入在胶层、电极和聚酰亚胺薄膜中，具有柔韧性好、变形量大以及面内各向异性等特点。国内外学者已经将MFC应用于仿生鱼的研究[12-13]，采用的基体材料分别为铝板或者碳纤维板。

目前，多数研究者采用一种基体材料直接研究仿生鱼的运动情况，尚未见到对仿生鱼的基体材料进行研究的文献。笔者研究基体材料对仿生鱼尾的影响。根据材料的性质，可分为各向同性和各向异性材料。它们的主要区别在于弹性模量的表示方法不同，而弹性模量相比较密度而言对仿生鱼的振动行为影响更大。笔者基于BCF模式设计出一种柔性复合型仿生鱼尾，并分析基体材料的弹性模量对仿生鱼尾振动的影响。首先，模拟鱼尾结构，优化模型，分析并确定了其振动模态；然后，通过改变基体材料的弹性模量来研究材料对鱼尾振动位移的影响；最后，制备基体材料，设计出鱼尾并进行振动测试，以验证仿真模型的合理性。

1 仿生鱼尾结构设计

仿生鱼尾分为驱动和尾鳍两部分。驱动部分选用的驱动元件是MFC(M8528-P1)，具体参数如表1所示。整个鱼尾结构示意图如图1所示，这种材料具有逆压电效应，可产生横向 (图1所示1(z)方向)伸缩变形。考虑鱼尾运动多为左右平动 (图1所示3(x)方向)，则在MFC底部增加基板，使整个机构产生弯曲振动。

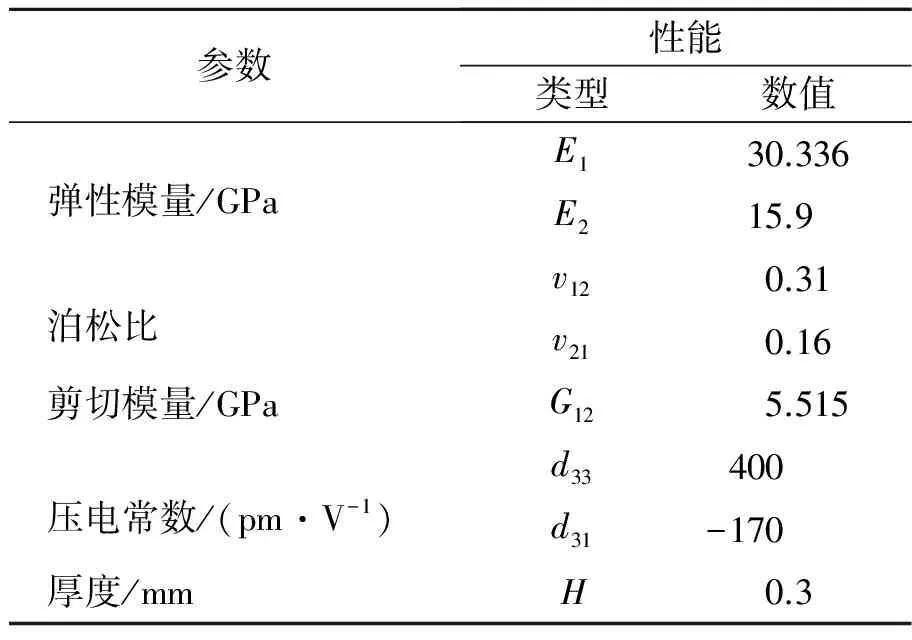
表1 MFC的性能参数

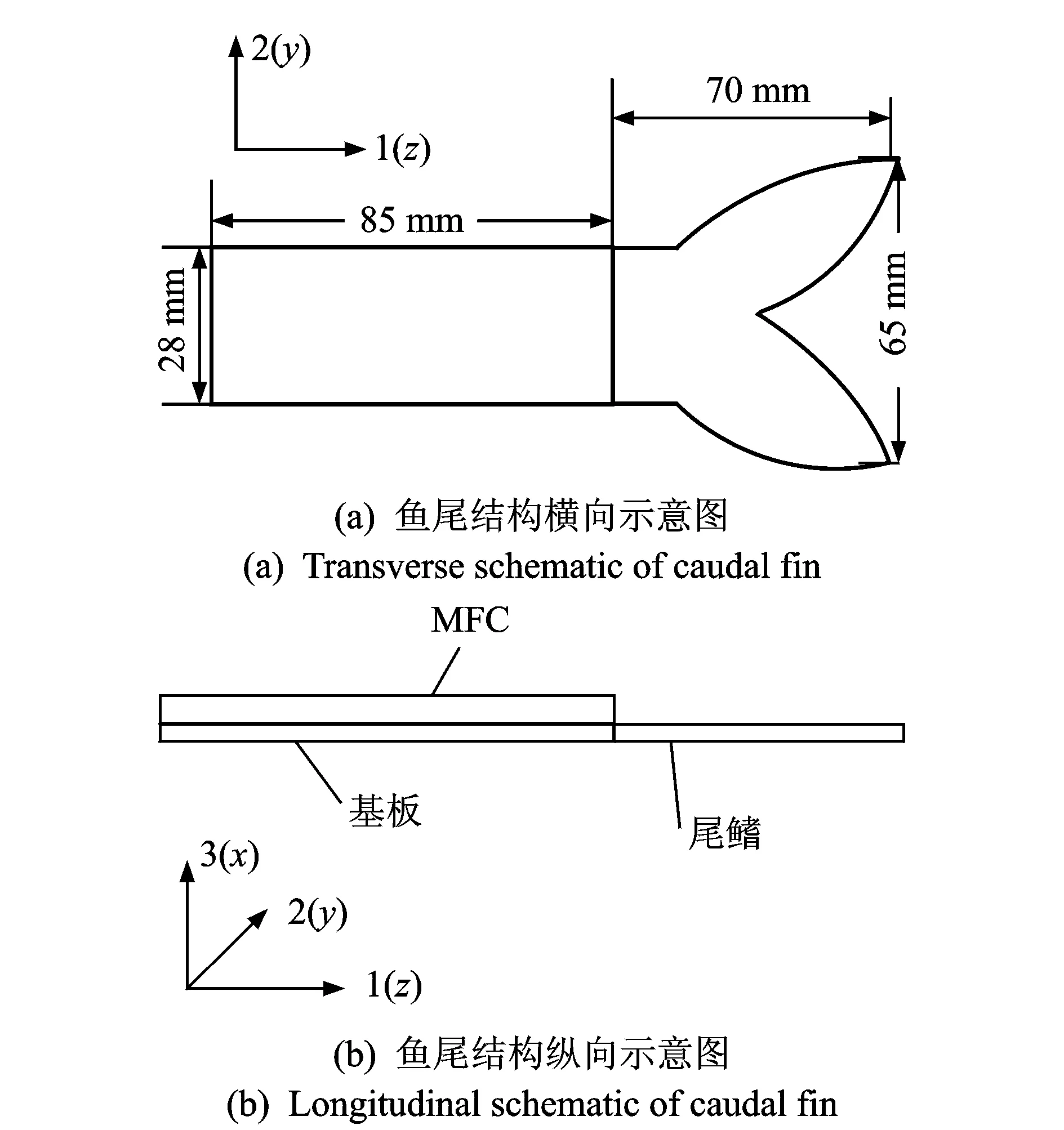
图1 鱼尾结构示意图Fig.1 Diagram of tail structure

2 鱼尾仿真计算

为研究鱼尾振动行为，在COMSOL Multiphysics有限元软件中根据如图1所示的鱼尾的预设尺寸建立三维模型。其中，驱动部分(具有MFC部分)的厚度为0.5 mm，尾鳍厚度为0.2 mm。由于鱼尾设计中的厚度远小于长度和宽度值，因此鱼尾可被作为一个薄板来考虑，且驱动元件产生的位移远大于其厚度值，属于大变形，因此在计算过程中考虑运用几何非线性特性。网格作为仿真计算的一个重要因素，直接影响结果的收敛性和计算精度，因此整个网格尺寸都采用较细化划分。图2为有限元网格模型。这种网格既减少了计算量，又满足计算结果收敛的要求。根据BCF推进模式，鱼尾只占整条鱼的1/3，且一端固定不动，而另一端是自由的，因此可将其看作为一个悬臂结构。设定边界条件为鱼尾左端固定约束，其余部分自由。

图2 鱼尾有限元模型Fig.2 Finite element model of caudal fin

为了具体分析弹性模量对鱼尾摆动位移的影响，在基板和尾鳍的外表面选取贯穿整个鱼尾的一条截线，如图3所示。整个模拟过程处于空气中，提供给MFC为700 V无偏置的峰峰值电压，由此分析弹性模量对鱼尾振动位移的影响。

图3 鱼尾的三维截线图Fig.3 3D sectional diagram of caudal fin

首先, 分析基体为铝板的鱼尾振动情况。铝板的弹性模量为70 GPa，密度为2 700 kg/m3，泊松比为0.33，此时鱼尾共振频率为12.2 Hz，在此频率下截线上各点总位移的一维图如图4所示，其中最大振动位移为6.578 8 mm。然后, 分析弹性模量为20 GPa，泊松比为0.33，密度为1 000 kg/m3的各向同性材料在共振频率为13.8 Hz时，振动位移为6.377 3 mm。最后，选取基体为相同密度和泊松比的弹性模量分别为15，10和3 GPa三种各向同性材料，在各自共振频率为13.1，11.7和9.9 Hz时，对应的振动位移分别为6.532 8，7.040 6和6.767 8 mm，这些截线上的位移如图5所示。通过图 5各条曲线进行对比发现，在材料具有相同密度和泊松比的条件下，随着弹性模量的减小，振动位移先增大后减少，在弹性模量为10 GPa时，各向同性材料位移达到最大，此材料适合于本结构模型。

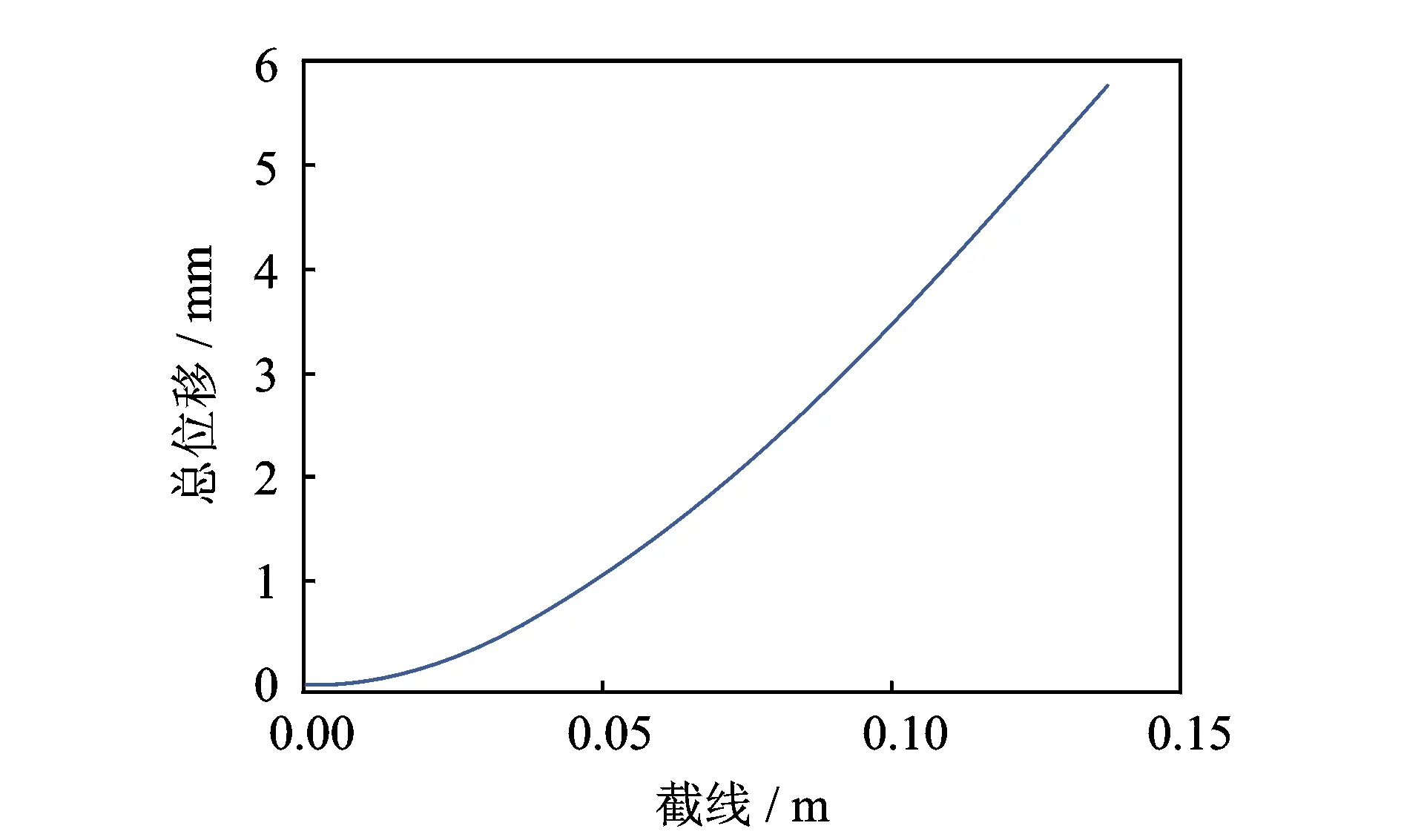
图4 基体为铝板截线上各点位移Fig.4 Displacement of caudal fin on the cutting line for the aluminum as the substrate

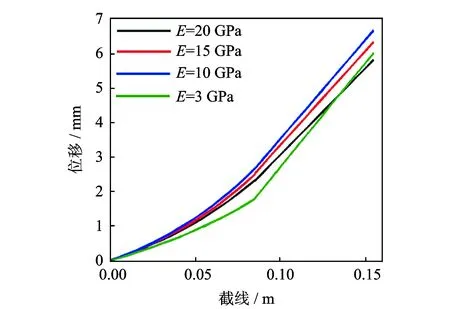
图5 各向同性材料弹性模量分别为20，15，10和3 GPa的位移图Fig.5 Displacement of caudal fin based on different elastic modulus of isotropic materials

但是质量轻、隐身性强且要满足弹性模量为10 GPa的各向同性材料不易寻找，而该弹性模量的复合材料屡见不鲜。为了与各向同性材料进行对比，采用弹性模量为表2所示的4种复合材料作为基体来模拟鱼尾的振动情况。基体为复合材料1，2，3，4的鱼尾在共振频率分别为12.5，11.3，8.7和7 Hz时相对应的振动位移分别为2.874 5,3.819 1,5.856和4.411 3 mm，这些截线上位移如图6所示。对图6中各条曲线进行对比，同样是弹性模量为10 GPa的材料位移最大，在一定弹性模量范围内存在适合本模型的弹性模量。图7为以上各向同性和各向异性材料的不同弹性模量在共振情况下对应的振动位移。

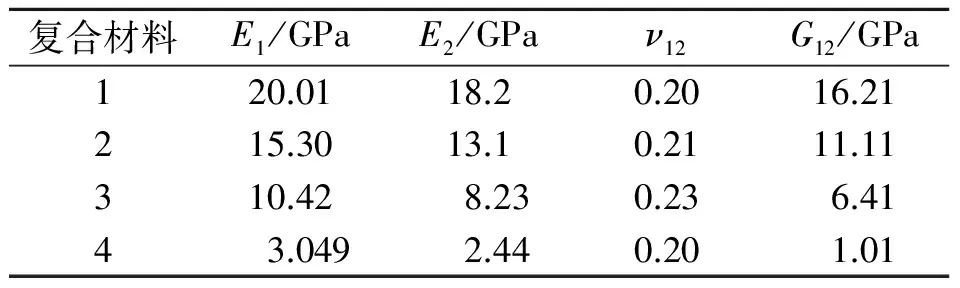
表2 复合材料性能参数

图6 基体材料为不同复合材料弯曲位移Fig.6 Displacement of caudal fin for different composites as the substrate

图7 不同弹性模量在共振情况下振动位移Fig.7 Resonance vibration displacement about different elastic modulus

根据图6得到复合材料3为基体的鱼尾变形最大，基体为复合材料4的鱼尾在基板与尾鳍交接处突变最大，因此给出采用基板为复合材料3、尾鳍为复合材料4的组合鱼尾，并且得到在共振频率为8.5 Hz时鱼尾振动的最大位移为9.928 3 mm，其截线上各点位移如图8所示。

图8 基板材料为复合材料3、尾部材料为复合材料4截线上各点位移Fig.8 Displacement of caudal fin on each point based on composite material 3 as the substrate and composite material 4 as the fin

图9为基体材料分别为铝、复合材料1和2构成的鱼尾弯曲位移图，可见，对于本模型结构复合材料3和4是最适合的。

图9 基体材料分别为铝板和复合材料的弯曲位移Fig.9 Displacement of caudal fin based on the aluminum and composites

3 鱼尾振动实验

在实验中采用玻璃纤维增强复合材料，它是用玻璃纤维或其织物以及增强合成树脂，通过涂布、注塑、挤塑和层压等方法加工成形，其重量轻、比强度高，具有各向异性的特点。复合材料3是由环氧树脂和厚度为0.16 mm玻璃纤维布制成的玻璃纤维环氧增强复合材料。复合材料4是由聚氨酯和厚度为0.1 mm玻璃纤维布制成的玻璃纤维聚氨酯增强复合材料。各性能参数如表2所示。鱼尾驱动部分是由玻璃纤维环氧增强型复合材料与MFC(具有压电特性的实际长度和宽度分别为85 mm和28 mm)组合而成，并在真空箱中用高剪切强度环氧树脂粘结，使整体厚度控制在0.6 mm左右。尾鳍采用玻璃纤维聚氨酯增强型复合材料，结构如图10所示。将鱼尾固定在夹具上，利用信号发生器和低频功率放大器给MFC施加电压，采用CCD激光位移传感器测量鱼尾振动的MFC末端和鱼尾末端的最大位移。整个鱼尾振动过程通过摄录机记录，整个实验设备如图11所示。

图10 实验结构图Fig.10 Experimental structure diagram

图11 鱼尾振动实验Fig.11 Vibration experiment of the caudal fin

图12 驱动部分MFC末端位移Fig.12 Displacement of end of MFC

考虑到MFC的允许工作电压范围为-500～1 500 V，无直流偏置电压最大峰峰值输入电压为1 kV，具有直流偏置最大峰峰值输入电压为2 kV。本实验采用无直流偏置最大峰峰值输入电压为700 V。图12为峰峰值电压分别为300，400，500，600和700 V、在5～15 Hz范围内、不同频率MFC末端位移图。根据振动理论中共振时位移最大的特点，由图12可以看出,共振频率为9 Hz、在700 V峰峰值电压下最大位移值为3.244 mm。

图13显示尾部从动部分末端位移量和变形角度。按照上述实验方法测量，得到最大位移为7.212 3 mm，最大偏转角度为28.37°。虽然实验结果与仿真结果有一定的误差，但是在允许范围内，验证了该仿真模型的合理性，为进一步优化结构提供了理论基础。

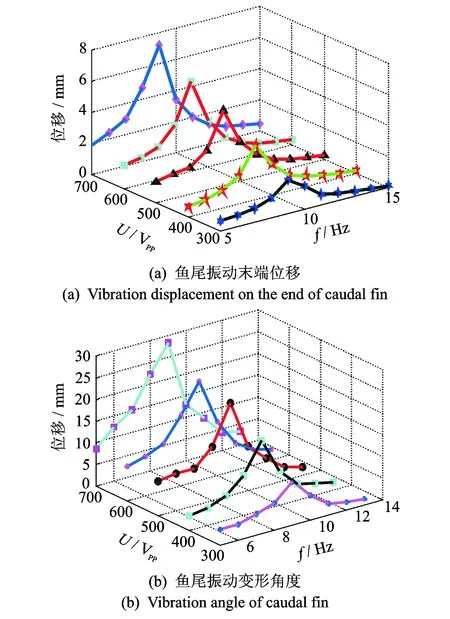
图13 鱼尾振动分析Fig.13 Analysis of caudal fin

4 结束语

主要讨论了不同的基体材料对鱼尾振动的影响。提出了一种采用粗压电纤维复合材料驱动的仿生鱼尾，利用仿真软件建立了数学模型，采用改变基体材料的弹性模量方式分析了其对鱼尾摆动位移的影响，得出了复合材料比各向同性材料更适合作为本模型的基体材料。通过对制备出的基体材料进行振动实验，验证了仿真的正确性，确定了玻璃纤维环氧增强复合材料为基板，玻璃纤维聚氨酯增强复合材料为尾鳍对于本设计的合理性。

[1] Breder C M. The locomotion of fishes[J]. American Zoologist, 1926,4:159-297.

[2] Webb P W. Form and function in fish swimming[J]. American Zoologist, 1984,251(1):58-68.

[3] Webb P W. Body form locomotion and foraging in aquatic vertebrates[J]. American Zoologist, 1984,24:107-120.

[4] Sfakiotakis M, Lane D M, Davies J B C. Review of fish swimming modes for aquatic locomotion[J]. IEEE Journal of Oceanic Engineering, 1999,24(2):237-252.

[5] Azuma A. The biokinetics of flying and swimming[M]. Aeronautical Engineering, Reston VA: AIAA, 2006:5-200.

[6] Webb G, Wilson L. Adaptive control of shape memory alloy actuators for underwater biomimetic applications[J]. Aiaa Journal, 2000,38(2):325-334.

[7] Shinjo N, Swain G W. Use of a shape memory alloy for the design of an oscillatory propulsion system[J]. IEEE Journal of Oceanic Engineering, 2004,29(3):750-755.

[8] Xu Xinsheng, Sun Faming. The control and optimization design of the fish-like underwater robot with the aid of the giant magnetostrictive material actuator[J]. Journal of Vibration and Control, 2009,15(10):1443-1462.

[9] Sun Faming, Xu Xinsheng. Non-linear vibration and dynamic characteristic of fish-like robot controlled by GMM actuator[J]. Journal of Intelligent Material Systems and Structures, 2009,20(12):1503-1513.

[10] Aureli M, Kopman V. Free-locomotion of underwater vehicles actuated by ionic polymer metal composites[J]. IEEE-ASME Transactions on Mechatronics, 2010,15(4):603-614.

[11]Peterson S D, Porfiri M. A particle image velocimetry study of vibrating ionic polymer metal composites in aqueous environments[J]. IEEE-ASME Transactions on Mechatronics, 2009,14(4):474-483.

[12]Erturk A, Delporte G. Underwater thrust and power generation using flexible piezoelectric composites: an experimental investigation toward self-powered swimmer-sensor platforms[J]. Smart Material and Structure, 2011,20(12):5013-5024.

[13]Shintake J, Aiguo M, Shimojo M. A novel propulsion method of flexible underwater robots[C]∥2011 IEEE/RSJ International Conference on Intelligent Robots and Systems. San Francisco: [s.n.], 2011:4735-4740.

*国家自然科学基金资助项目(51175250)；中央高校基本科研业务费专项资金资助项目(NJ2013006，NS2012033，CXLX12_0144)；江苏省普通高校研究生科研创新计划资助项目(CXLX12_0144)；高等学校创新引智计划资助项目(B12021)；江苏高效优势学科建设工程资助项目(PAPD)

2013-05-13；

2013-07-10

10.16450/j.cnki.issn.1004-6801.2015.01.002

TH111； TH14

官源林，男，1983年5月生，博士研究生。主要研究方向为小型仿生鱼尾研究。曾发表《基于MFC的复合型仿生鱼尾的振动性能》(《振动、测试与诊断》2013年第33卷增刊2)等论文。 E-mail:guanyuanlin201@163.com