考虑多间隙的帆板式展开机构动力学分析*

谷勇霞， 杨天夫， 郭 峰

(1.北京工商大学材料与机械工程学院 北京，100048) (2.清华大学摩擦学国家重点实验室 北京，100084)



考虑多间隙的帆板式展开机构动力学分析*

谷勇霞1， 杨天夫2， 郭 峰2

(1.北京工商大学材料与机械工程学院 北京，100048) (2.清华大学摩擦学国家重点实验室 北京，100084)

在轨运行的大型航天器都含有太阳翼等帆板式展开机构，这种机构发射时处于折叠状态，在轨时处于展开结构状态。帆板之间的铰链间隙对于航天器系统的在轨动力学行为会产生很大影响。利用Adams多体动力学分析软件构造了由卫星本体、帆板式展开机构、间隙铰链和柔性帆板组成的多间隙帆板式展开动力学模型，数值分析了在多间隙作用下展开过程的系统动力学特性，比较了不同间隙数目对系统动力学特性的影响。通过分析展开过程中铰链轴与孔体的接触碰撞力，发现间隙的增多会使轴孔碰撞更加强烈，次数更加频繁。通过分析帆板展开过程中的角加速度变化情况，得到了间隙铰碰撞对展开机构运行稳定性的影响。

航天器; 可展机构; 间隙; 碰撞

引言

随着航天工程的迅速发展，空间可展结构越来越多地应用在各种航天器上，其动力学性能的研究日益受到国内外航天部门和学者的重视。近年来，对空间可展结构动力学的仿真研究(包括可展天线、空间机械臂、太阳能帆板和桁架式骨架结构等)越来越多。可展结构中普遍存在运动副间隙和构件的柔性变形都将对系统的动力学特性产生重要影响[1]。

太阳能帆板是现代大型航天器中的必备组件，为航天器提供主要能源。发射时太阳能帆板一般呈收拢状态，直到航天器与运载工具分离之后，帆板展开并锁定。刚性太阳能帆板是一种典型的帆板式展开结构，蜂窝基板通过活动铰链相互连接，铰链中不可避免地存在间隙。间隙会导致卫星定位、定向、姿态失稳和频率漂移等现象发生[1-3]，对系统的运行状态影响极大。文献[4-8]对于含间隙太阳能帆板结构进行研究，在实验方法方面取得了一定成果。文献[9]对单板单间隙系统的研究结果表明，间隙是帆板产生振动的重要原因且间隙的增大会导致振动加剧。文献[10]把阻尼、摩擦和重力势对含间隙太阳能帆板结构的影响进行了研究。目前的研究多集中在单板单间隙或双板单间隙的条件下，而针对多板多间隙的情况研究较少。

为了深入分析太阳能帆板可展结构在伸展过程中的动力学特性，笔者以多体系统动力学理论为基础[11-14]，建立了含有双间隙双帆板的帆板式展开机构的动力学仿真模型，针对不同的间隙分布形式进行多体动力学仿真实验研究。

1 动力学建模

图1为展开的模拟太阳能帆板伸展机构的仿真模型。整个实体模型由内、外两块帆板通过连接架、铰链机构、带轮同步机构与航天器本体相连接。实际的太阳能帆板伸展机构初始状态由压紧装置将帆板压在航天器本体侧壁上，使整个机构处于收拢状态。当机构处于初始位置时，内帆板和本体侧壁之间的夹角为α=0°，内、外帆板之间夹角为β=0°。在展开终了位置即帆板锁定后，相应的夹角分别为α=90°，β=180°。

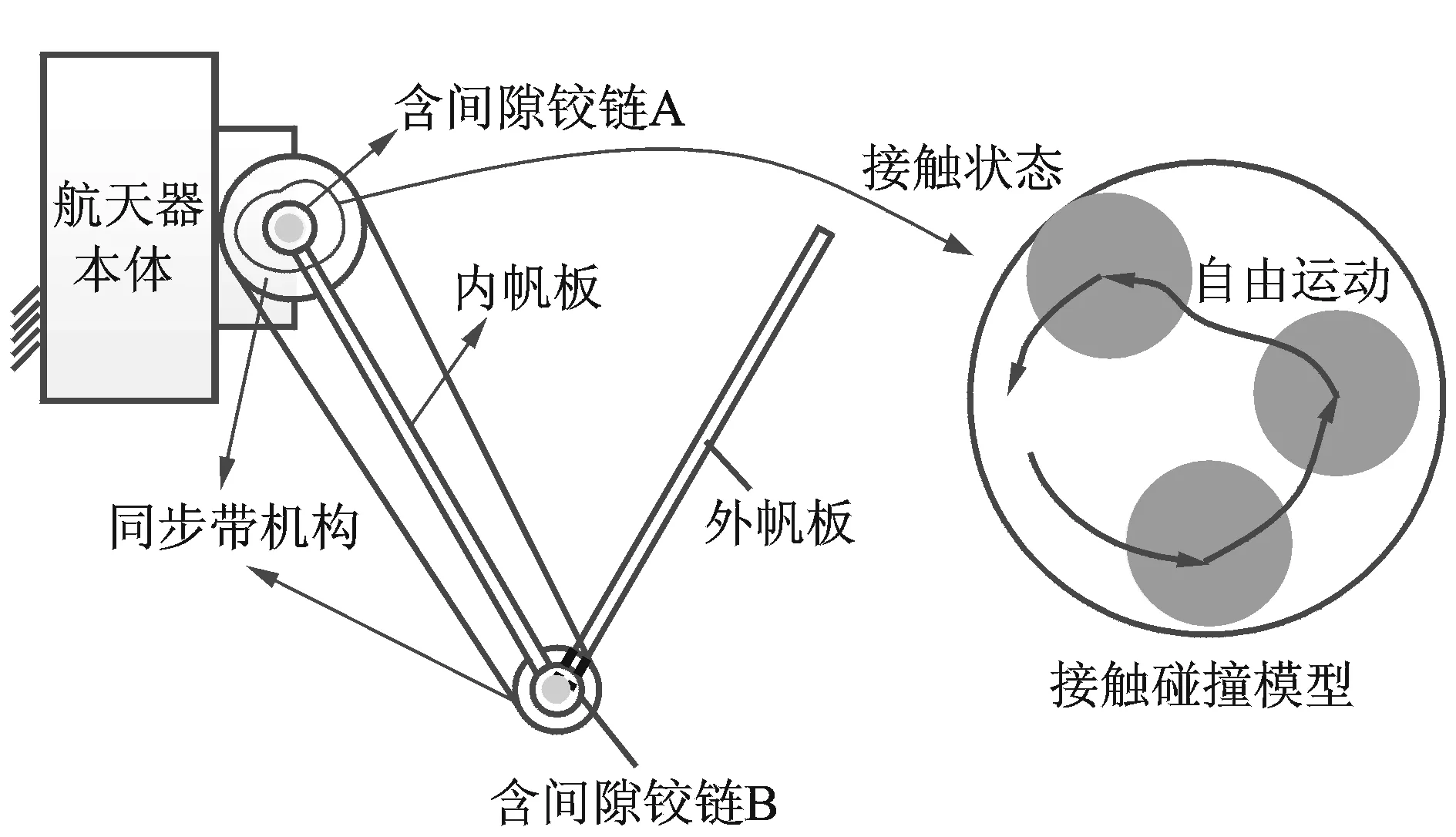
图1 帆板展开机构原理图Fig.1 The schematic diagram of deployable mechanism

模拟太阳能帆板可展结构展开过程主要分为3个阶段：释放、同步展开和锁定。释放阶段含有过渡过程，动力学行为较为复杂，涉及刚体和弹性体的碰撞问题，故这里主要研究模拟太阳能帆板可展结构同步展开阶段的动力学性能，对锁定阶段的动力学响应进行了初步研究。

1.1 含间隙的多体动力学模型

本研究使用的间隙模型是经典的接触碰撞模型，轴孔之间由碰撞引起的动力学行为归结为“自由运动-接触变形”两种状态。对于自由状态，几何接触Φ=0，不起作用，相应的拉式乘子为0，即在此状态下不含任何约束。此时系统的动力学方程[15-16]可表示为

(1)

其中：M，K，Φq和Q分别为系统的广义质量阵、刚度阵、约束方程的雅克比矩阵和广义速度的二次项及广义力阵；λ为广义拉式乘子列向量。

在接触状态下，间隙副的接触产生了约束条件的变化，解除系统的运动学约束，用接触力和摩擦力约束取代。在发生碰撞的物体间引入接触力模型，系统的动力学模型[15-16]变化为

(2)

其中：FI和Ff分别为接触力和摩擦力相对于广义坐标的广义力阵。

在实际工况下，间隙铰的碰撞分布在整个轴向方向上，为了便于计算，将径向碰撞力简化为两个，分别作用在铰的两端中心位置。间隙铰采用的非线性等效弹簧阻尼法向接触力模型为

(3)

其中：Kn为系统的等效刚度；e为Hertz接触力指数，取e=1.5；δ为两接触物体之间的法向穿透深度；C(δ)为关于系统阻尼系数的函数。

设dmax为碰撞最大穿透深度；Cmax为对应的最大阻尼系数，则系统的阻尼函数C(δ)为

(4)

对于斜碰撞时铰内产生的摩擦力而言，当铰承受的载荷不大时，经典的库仑摩擦力模型具有足够的精度。摩擦力的大小[17]为

Ff=-μdFnsgn(v) (v≠0)

(5)

其中：Ff为接触处滑动摩擦力；μd为动摩擦因数；v为接触点处相对滑移速度。

将式(3)和式(5)代入式(1)和式(2)，完成了含间隙旋转铰的多体动力学建模。

1.2 同步机构建模

同步带联动机构是目前常用的同步展开控制机构，它由与展开机构铰链相固定的大小带轮及以带轮导向和支撑的同步带组成。每两块帆板之间安装一个同步带联动机构以保证帆板的同步运动。导索环实际上是两个同步带轮，其转动轴分别与两块帆板的转动轴固连在一起，因此同步带的转动分别和与其相连的帆板相同。同步带以一定的张紧力绕在两个同步带轮上，随着同步带轮的转动而转动，张紧力是为了防止同步带跳齿和打滑。

根据绳索联动机构的工作原理可知，机构提供的力矩是由内外帆板板间运动不同步引起的；因此，可以将同步机构对帆板的作用力等效为一被动控制系统力矩，表达式为

(6)

1.3 柔性帆板建模

太阳能帆板可展结构是典型的多体系统，展开过程中构件不仅要发生大范围的相对运动，其本身同时又产生弹性变形；因此，系统中各构件的位置、姿态和弹性变形等存在相互耦合作用。此外，帆板伸展机构在展开过程中，由于构形的变化，在各个位置的结构固有频率也随之变化。如何结合太阳能可展结构的特点，利用柔性多体系统动力学理论，分析研究帆板可展结构伸展过程中的动力学特性，对包括太阳能帆板在内的空间可展结构的设计和控制策略的实施具有重要的理论价值和工程实际意义。

笔者采用Adams软件有限元划分插件AutoFlex对内、外帆板进行网格离散化，将内帆板划分为742个单元、1 486个结点，将外帆板划分为756个单元、1 514个结点。

2 数值算例

图2为收拢状态的太阳能帆板伸展机构的Adams模型。整个实体模型由内、外两块帆板通过连接架、铰链机构、带轮同步机构与航天器本体相连接。帆板采用Adams软件的有限元划分插件AutoFlex，采用笔者提出的方法进行网格离散化。间隙铰内的作用力和同步机构的控制力矩则根据笔者提出的方法在Adams内进行编程计算。该模型可以模拟在轨太阳能帆板的展开-锁定过程。两个铰链机构的母铰和公铰采用转动铰连接，其他各零部件之间的约束关系均为固定约束。帆板和带轮的材料为铝，其他材料均为45#钢。内、外帆板的主要参数如表1所示。

图2 收拢状态的太阳能帆板伸展机构Adams模型Fig.2 Adams model of solar panels in folded state

太阳能帆板释放后，由安装在铰链机构中的钢丝扭簧驱动帆板展开，整个机构有两个铰链，故需要两个扭簧元件。Adams软件提供标准的扭簧连接件(Torsion-Spring)，按照扭簧设计手册，选取材料为65Mn，内径D1=10 mm，承受Ⅲ类载荷(受静载荷以及变载荷作用次数在1×103次以下)，预紧转角φ0=120°，最大工作转角φmax=180°，工作转角φmin=90°的扭簧，经过计算，扭簧的扭转刚度为kT=108.98 N·mm/rad，内帆板与本体之间的固定端扭簧预紧角的预紧扭矩T0A=399.42 N·mm,T0B=570.6 N·mm。

表1 内、外帆板主要构件的质量和惯量参数

Tab.1 Mass and inertia parameters of the main components

参数内帆板外帆板长度/mm290300宽度/mm150150厚度/mm22质量/kg0．238380．2466Ix/(kg·mm2)2117．6092311．875Iy/(kg·mm2)1670．725961849．5822Iz/(kg·mm2)447．04196462．4572

为了验证间隙数量对于系统性能的影响，笔者分别采用理想铰链、A处单间隙、B处单间隙和AB处双间隙4种方式进行了一个周期的展开动力学仿真。含间隙铰链的间隙大小为δ=R-r=0.5 mm，轴孔之间的接触刚度K=5×104N/mm，金属表面摩擦因数μd=0.2，接触阻尼系数C=0.01 N·s/mm，仿真总时间t=1 s。

3 仿真结果分析

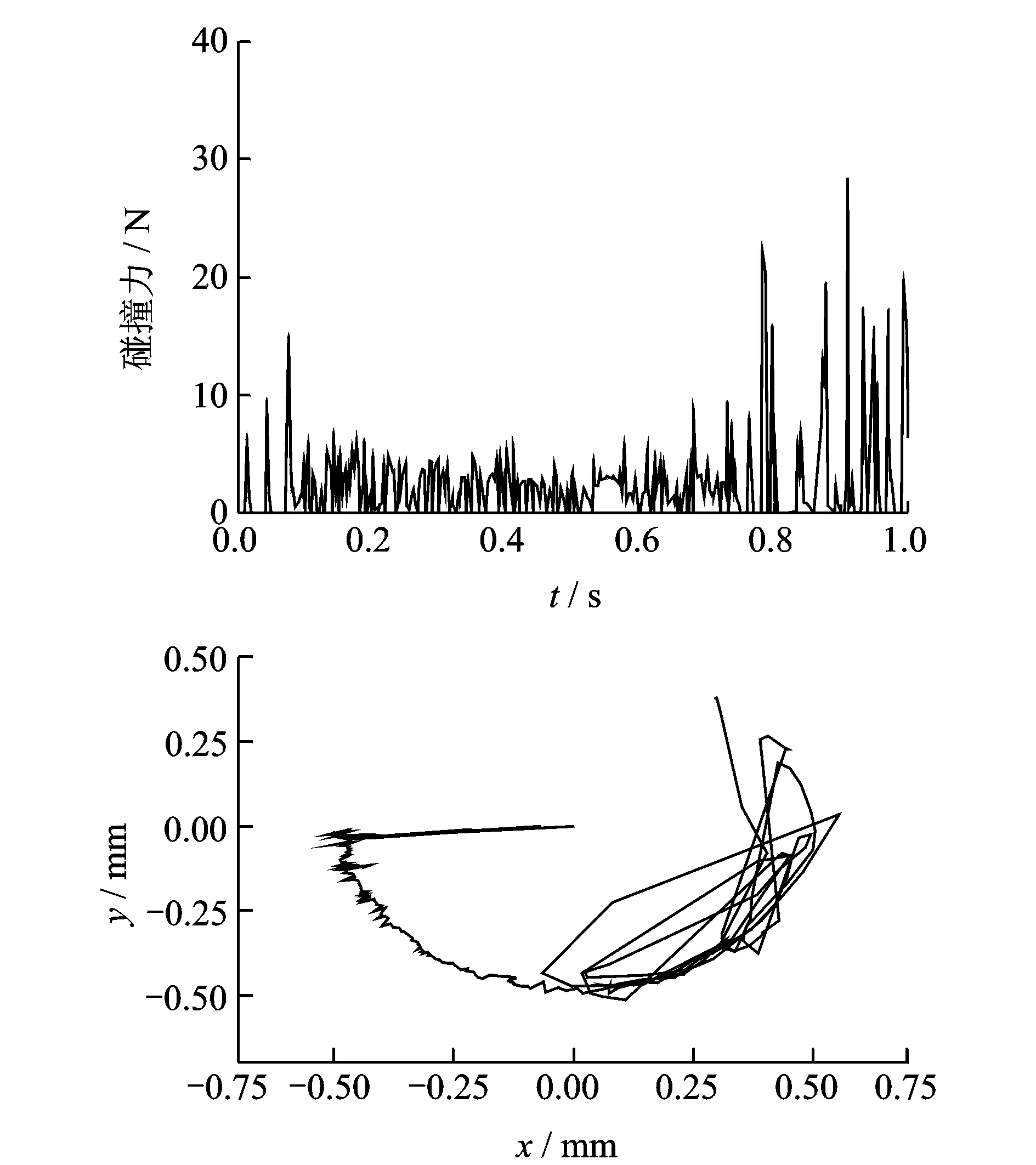
图3 A处单间隙的碰撞力和质心轨迹Fig.3 Impact force and centroid trajectory with single clearance in joint A

图4 B处单间隙的碰撞力和质心轨迹Fig.4 Impact force and centroid trajectory with single clearance in joint B

图5 双间隙A处碰撞力和质心轨迹Fig.5 Impact force and centroid trajectory of joint A with double clearances

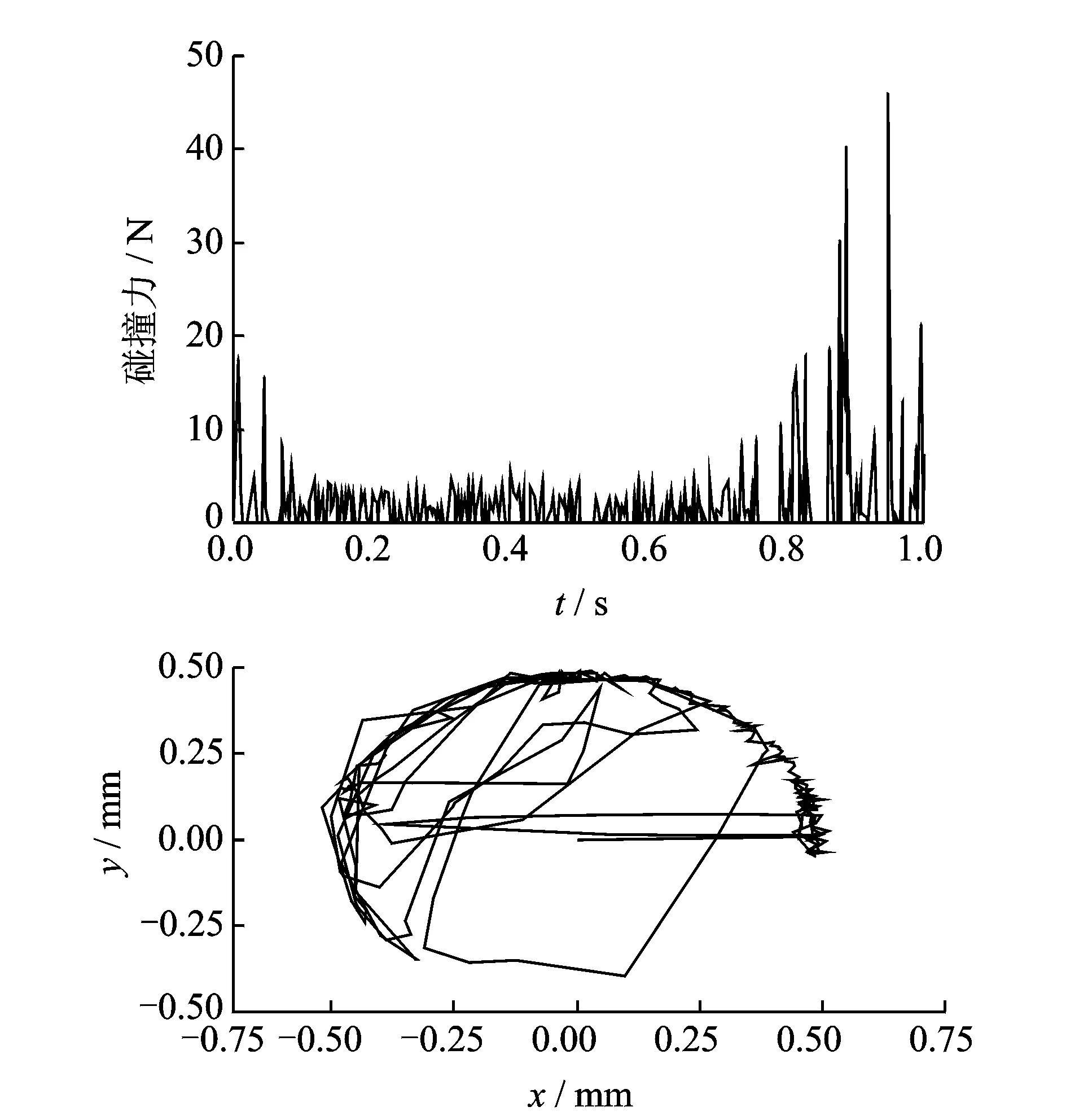
图6 双间隙B处碰撞力和质心轨迹Fig.6 Impact force and centroid trajectory of joint B with double clearances

图3～6分别为A处单间隙、B处单间隙、双间隙根铰链A和双间隙中间铰链B的碰撞力和质心轨迹图。随着展开过程的推移，碰撞力和碰撞频率都明显开始增大；展开过程进行到0.8 s左右时，展开机构开始减速进入锁定状态，碰撞力幅值开始明显增大。同文献[10]的仿真结果对比发现，在柔性帆板的影响下，间隙铰链的碰撞次数和碰撞强烈程度都明显减小。从图3～6的对比看出，根部铰链A处的碰撞主要集中于上半圆周部分，而中间铰链B的碰撞主要集中于下半圆周部分，这是由于展开时帆板的转动方向不同造成的。根部铰链A同时受到双帆板的影响，碰撞的次数和幅值都要高于中间铰链B处，且间隙数目增多带来的碰撞力增大的现象在锁定过程中更为明显。

表2为碰撞力统计情况可以看出平均碰撞力在间隙增多时虽然没有明显变化，但双间隙的碰撞力最大值明显高于单间隙的情况，且碰撞次数显著增长。这说明间隙数目的增多给系统的动力学响应带来了更多不确定性，碰撞冲击的加强更容易造成系统失效与故障产生。

表2 碰撞力情况统计

间隙数目的增多对于轴孔之间的运动关系有显著影响，销轴与销孔的碰撞将直接对帆板的展开行为造成冲击。图7～9为不同间隙数目情况下内外板展开时的角加速度变化曲线。可以看出，根部铰链A处的间隙对于加速度波动幅值影响更大，而内板的加速度波动强于外板，该结论与轴孔碰撞的现象相吻合。随着间隙的引入和增多，双间隙作用下的碰撞力与A处单间隙相比有小幅上升，加速度冲击的幅值由8×104rad/s2增加到8×105rad/s2，增大10倍左右。振动频率也有所上升，帆板的运动稳定性进一步下降。

图7 A处单间隙情况的加速度曲线Fig.7 Acceleration curve with single clearance in joint A

图8 B处单间隙情况的加速度曲线Fig.8 Acceleration curve with single clearance in joint B

图9 双间隙情况的加速度曲线Fig.9 Acceleration curve with double clearances

4 结束语

建立了多间隙的太阳能帆板展开模型。对太阳能帆板在不同间隙数目作用下的在轨展开行为进行了动力学分析。算例仿真结果表明，在展开过程中，多间隙的引入增加了动力学分析的复杂性，轴孔的碰撞次数和碰撞力都显著增长。这种现象使帆板在展开过程中承受更大和更频繁的加速度冲击，将导致系统的不稳定甚至失效。间隙的增多给太阳能帆板的展开过程带来了更复杂的特性，导致系统的不稳定性增强，给理论分析带来了更大的困难。相比于中间铰链，固定的根部铰链间隙对系统的动力学特性影响更为显著。对含多间隙的帆板式展开机构的动力学研究将有助于提高航天可展机构的设计和动力学分析水平。

[1] 马兴瑞,王本利,苟兴宇,等.航天器动力学:若干问题进展及应用[M].北京:科学出版社,2001:299-312.

[2] 李君兰，阎绍泽，吴小燕，等.太阳翼可展结构频率的重力势影响[J].清华大学学报:自然科学版,2012,52(1):25-30.

Li Junlan, Yan Shaoze, Wu Xiaoyan, et al. Effects of gravity potential on frequency of deployable panel structures[J]. Journal of Tsinghua University: Natural Science Edition, 2012,52(1):25-30. (in Chinese)

[3] 吴小燕,杨运强,吴嘉宁,等.带有故障的太阳电池阵动力学模拟及性能评价[C]∥2011年全国机械动力学学术大会.杭州:中国振动工程学会机械动力学专业委员会, 2011.

[4] 阎绍泽，陈鹿民，吴德隆，等.空间可展结构非线性动力学特性实验研究[J].宇航学报,2002(4):1-3,11.

Yan Shaoze, Chen Lumin, Wu Delong, et al. Dynamic experiment of a space deployable truss structure with joint clearances[J]. Journal of Astronautics, 2002(4):1-3,11. (in Chinese)

[5] 陈鹿民，阎绍泽，金德闻，等.含间隙铰空间可展桁架结构的动力学实验[J].清华大学学报:自然科学版,2003(8):1027-1030.

Chen Lumin, Yan Shaoze, Jin Dewen, et al. Dynamic experiment of a space deployable truss structure with joint clearances[J]. Journal of Tsinghua University: Natural Science Edition, 2003(8):1027-1030. (in Chinese)

[6] Xun Jian, Yan Shaoze. A revised Hilbert-Huang transformation based on the neural networks and its application in vibration signal analysis of a deployable structure[J]. Mechanical Systems and Signal Processing, 2008,22(7):1705-1723.

[7] 荀剑，阎绍泽.基于小波变换的含间隙太阳能帆板动力学试验分析[J].清华大学学报：自然科学版,2006,46(11):1844-1847.

Xun Jian，Yan Shaoze. A wavelet transform based analysis of vibration signals from a solar array with clearance[J]. Journal of Tsinghua University: Natural Science Edition, 2006,46(11):1844-1847. (in Chinese)

[8] 阎绍泽，蔡仁宇，丁袆，等.基于ADAMS的太阳电池阵动力学模拟参数化建模系统[J].电子机械工程,2011(3):18-23.

Yan Shaoze, Cai Renyu, Ding Yi, et al. Parametric modeling system for dynamic simulation of sollay array based on ADAMS[J]. Electro-Mechanical Engineering, 2011(3):18-23. (in Chinese)

[9] Zhang Lixin, Bai Zhengfeng, Zhao Yang, et al. Dynamic response of solar panel deployment on spacecraft system considering joint clearance [J]. Acta Astronaut, 2012(81):174-185.

[10]Li Junlan, Yan Shaoze , Guo Feng, et al. Effects of damping, friction and gravity on dynamic performance of a deployable mechanism with clearances[J]. Journal of Mechanical Engineering Science, 2012,227(8):1791-1803.

[11]陈烈民.航天器太阳翼的结构和机构.中国航天器工程进展[M]. 北京：中国科学技术出版社, 2005:356-374.

[12]赵坚成.半刚性太阳电池阵结构[J].中国空间科学技术，1982,4:48-53.

Zhao Jiancheng. Structure of semi-rigid solar panel[J]. Chinese Space Science and Technology, 1982,4:48-53. (in Chinese)

[13]陈烈民.卫星太阳翼展开运动分析[J].中国空间科学技术，1992(4):21-26.

Chen Liemin. Analysis of deployment motion of satellite solar wing[J]. Space Science and Technology,1992(4):21-26. (in Chinese)

[14]王天舒,孔宪仁,王本利，等.太阳帆板绳索联动同步机构的机理和功能分析[J]. 宇航学报，2000(7):29-38.

Wang Tianshu, Kong Xianren, Wang Benli, et al. The research on principle and function of closed loop configuration of solar arrays[J]. Journal of Astronautics, 2000(7):29-38. (in Chinese)

[15]Dubowsky S, Deck J F, Costello H. Dynamic modeling of flexible spatial machine systems with clearance connections[J]. ASME Journal of Mechanisms Transmissions and Automation in Design, 1987,109(1):87-94.

[16]Khemili I, Romdhane L. Dynamic analysis of a flexible slider-crank mechanism with clearance[J]. European Journal of Mechanics A/Solids,2008(27):882-898.

[17]Lankarani H M, Nikravesh P E. A contact force model with hysteresis damping for impact analysis of multibody systems[J]. Journal of Mechanical Design,1990(112):369-376.

*国家自然科学基金资助项目(11272171)

2014-04-16；

2014-06-12

10.16450/j.cnki.issn.1004-6801.2015.01.006

TH123

谷勇霞，女，1968年6月生，副教授。主要研究方向为机械设计及机械系统动力学、可靠性评估。曾发表《考虑谐波传动滞后的柔性空间机械臂运动精度》(《机械工程学报》2013年第49卷第23期)等论文。 E-mail: gyxchina@163.com