基于TGSVD的桥梁移动荷载识别及正则化矩阵选取*

陈 震， 余 岭

(1. 华北水利水电大学土木与交通学院 郑州，450045)(2. 暨南大学重大工程灾害与控制教育部重点实验室 广州，510632)



基于TGSVD的桥梁移动荷载识别及正则化矩阵选取*

陈 震1，2， 余 岭2

(1. 华北水利水电大学土木与交通学院 郑州，450045)(2. 暨南大学重大工程灾害与控制教育部重点实验室 广州，510632)

基于时域法(time domain method ，简称TDM)识别移动荷载理论，通过引入正则化矩阵，提出采用截断广义奇异值分解法(truncated generalized singular value decomposition，简称TGSVD)识别桥梁移动荷载。比较不同正则化矩阵对TGSVD识别结果影响，并与TDM识别结果进行比较，两轴移动荷载识别结果表明，正则化矩阵选取对TGSVD识别精度、鲁棒性等影响较大。当正则化矩阵选取适当，TGSVD采用弯矩和加速度响应均具有较高识别精度且识别结果受噪声干扰小。在测点类型单一或测点数量较小时优势更为突出，适宜于现场移动荷载识别，具有较强的工程应用价值。

桥梁； 移动荷载； 识别； 不适定性； 时域法； 截断广义奇异值分解法； 正则化矩阵

引言

移动荷载会引起桥梁疲劳损伤甚至破坏，由桥梁响应识别移动荷载是典型的结构动力学第二类反问题，由于测量响应的离散性并需要计算反卷积，这类问题具有明显的病态特征[1]。近年来，移动荷载识别有较大发展，提出很多新的方法。袁向荣等[2]通过梁振动响应曲线提出响应曲线滑动拟合法。Law 等[3]以时域法[4]和频时域法[5]为基础，将正则化方法应用于移动称重技术中。卜建清等[6]提出基于广义正交函数和正则化的移动荷载识别法。文献[1,7]采用样条函数逼近桥梁响应识别移动荷载。余岭等[8]提出采用预处理共轭梯度法识别移动荷载。陈锋等[9]采用模态置信准则对梁桥上移动荷载识别中的测点进行优化。文献[10-11]基于有限元理论采用形函数识别移动荷载。夏樟华等[12]结合健康监测系统识别移动荷载。余岭等[13]采用数值模拟和模型实验验证了时域法和频时域法的识别精度。

基于奇异值分解法(singular value decomposition ，简称SVD)思路，针对系数矩阵欠秩引起的不适定问题，Hansen[14]提出广义奇异值分解法(generalized singular value decomposition, 简称GSVD)。对于求解最小二乘问题，截断奇异值分解法(truncated singular value decomposition, 简称TSVD)的解不包含系数矩阵的数值零空间，即为正则化解。将TSVD的解一般化即为截断广义奇异值分解法的解。以时域法识别移动荷载为基础，模拟双轴车辆在简支梁桥上行驶过程，采用提出的TGSVD由桥梁弯矩响应或加速度响应识别桥面移动车载。TGSVD的识别精度和正则化矩阵的选取密切相关，笔者分别采用单位矩阵、双对角矩阵和三对角矩阵三类正则化矩阵，比较其对TGSVD识别精度和抗噪性能的影响。算例计算结果表明，单位正则化矩阵不能提高TGSVD的识别精度，采用双对角正则化矩阵和三对角正则化矩阵具有较高的识别精度，对改善病态识别问题的不适定性有良好效果。其中，双对角矩阵在所有识别工况中显示出良好的适应性和鲁棒性，在三种正则化矩阵类型中具有较好的竞争性。

1 基本理论

1．1 简支梁单荷载识别

Euler-Bernoulli梁长度为L，动荷载P以均匀速度c沿着梁面移动，如图1所示。图中直线为简支梁原轴线，弧线为简支梁在荷载作用下的变形。取梁单位长度质量为ρ，考虑粘性阻尼并取阻尼系数为C，简支梁抗弯刚度为EI，移动荷载运动方程为

(n=1,2,…,∞)

(1)

图1 简支梁单荷载识别模型Fig.1 Simply supported beam model for single force identification

由时域法识别移动荷载理论可知，简支梁上某位置任一时刻的弯矩响应和加速度响应可通过卷积积分得到，梁上x处t时刻的弯矩响应为

(2)

同理，梁上x处t时刻的加速度响应为

(3)

其中：

当已知桥面响应b和系统矩阵A，TDM识别移动荷载最终都可转化为逆问题的求解

AN×NBxNB×1=bN×1

(4)

其中：x为待识别的移动荷载；下标N为测点响应数；NB=L/cΔt为采样样本数。

1．2 TGSVD识别移动荷载

(5)

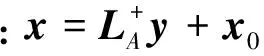
1．3 TGSVD正则化矩阵选取

为比较正则化矩阵对TGSVD识别精度和抗噪性能影响，分别选取单位矩阵L1、双对角矩阵L2和三对角矩阵L3为正则化矩阵。当选用L1正则化矩阵时，TGSVD退化为截断奇异值分解方法，L1，L2，L3分别为

(6a)

(6b)

(6c)

2 数值模拟

2．1 车桥仿真参数

采用文献[4]算例识别两轴移动荷载，比较正则化矩阵选取对TGSVD识别结果影响，并与采用TDM法识别移动荷载结果进行比较。双轴车载的前轴荷载和后轴荷载分别为

(7)

(8)

其中：车辆行驶速度c=40 m/s；两轴间距ls=8 m；简支梁跨度L=40 m；抗弯刚度EI=1.279×1011N·m2；单位长度密度ρ=12 000 kg/m；简支梁前三阶固有频率分别为3.2 ，12.8 ，28.8 Hz；采样频率取200 Hz；分析频段取为0～40 Hz。

噪声干扰下的桥梁弯矩响应或加速度响应为

(9)

识别误差评判标准为

(10)

其中：Error为相对百分误差；‖·‖为向量的范数；Ftrue为真实荷载；Fidentified为识别荷载。

2.2 不同正则化矩阵识别结果比较

在简支梁1/4跨长、1/2跨长和3/4跨长位置分别布设应变片和加速度计，即可测得对应位置的弯矩响应和加速度响应。通过选取不同位置弯矩响应和加速度响应组合，即可确定测点数量和测点类型不同时各识别方法的识别精度。

TDM识别结果表明，采用加速度响应识别移动荷载精度较高，而弯矩响应识别结果则不理想。分别采用单位矩阵L1、双对角矩阵L2和三对角矩阵L3作为正则化矩阵，比较TGSVD采用不同正则化矩阵时识别结果差别，进而选取最优正则化矩阵。

表1为两种工况仅由弯矩响应识别移动荷载时，TDM与TGSVD采用不同正则化矩阵识别结果比较。TDM识别误差很大，当噪声水平大于1%时，识别误差均超过100%，无法识别移动荷载。TGSVD识别精度较TDM有很大提高，在噪声水平小于10%时，识别精度均可接受，且其识别精度随正则化矩阵选取不同差异较大。3种正则化矩阵中，采用单位矩阵L1时识别误差最大，采用双对角矩阵L2和三对角矩阵L3识别精度较高。在噪声水平为1%，采用L2和L3作为正则化矩阵时，识别误差最大值仅为6.5%。

表1 TGSVD正则化矩阵选取识别误差比较

图2表明采用单位矩阵L1时，两轴车辆在前轴下桥和后轴上桥时刻识别结果与真实值偏差较大，精度较差，其余时段识别精度尚可接受，采用L2和L3能精确识别两轴移动荷载。图3表明当噪声水平增加到5%时，采用3种正则化矩阵识别精度均较噪声水平为1%时有所降低。在前轴下桥和后轴上桥时刻，采用L2和L3时识别结果也会出现轻微波动，且采用L2时波动较小，识别精度最高。数值仿真结果表明：TGSVD采用单位矩阵L1作为正则化矩阵时，识别精度较差；采用双对角矩阵L2和三对角矩阵L3识别精度较高。随着噪声水平的增加，在前轴下桥和后轴上桥时刻识别精度均会有所波动。采用L2时波动较小，能较好抑制由系统方程的不适定导致的识别误差，L2为3种正则化矩阵中最优正则化矩阵。

2．3 TDM与TGSVD识别结果比较

TGSVD采用不同正则化矩阵识别结果表明，采用L2和L3作为正则化矩阵时TGSVD识别精度较高，采用L1时不能降低由系统方程的不适定导致的识别误差，后面研究仅采用L2和L3作为正则化矩阵并比较TGSVD和TDM识别结果。由弯矩响应识别结果表明, TGSVD可仅由弯矩响应识别移动荷载，识别精度较TDM有很大提高。

图2 1%噪声时采用不同正则化矩阵弯矩响应识别结果比较(1/4，1/2和3/4跨长的3个弯矩响应)Fig.2 Comparison on identified results from bending moment responses by TGSVD with three different regularization matrixes when the noise is 1%

本部分重点研究由加速度响应或加速度响应和弯矩响应组合识别两轴移动荷载时，TGSVD和TDM识别结果差异。表2为4种工况分别采用加速度响应或弯矩和加速度组合响应识别移动荷载时，TDM与TGSVD识别结果比较。由表2可知，采用TDM识别移动荷载时，识别误差随噪声水平线性增加，绝大多数工况识别误差大于50%，最大误差值达到6 824%。采用TGSVD识别移动荷载时，识别误差随噪声水平增加略有增加，但增加幅值很小，尤其是采用L2正则化矩阵，当噪声水平从1%增加到10%时，误差增加幅值最大仅为2.4%(1/4，1/2跨长的2个弯矩响应和1/2跨长的1个加速度响应工况前轴识别结果)。TGSVD识别误差受噪声干扰影响很小，具有良好的鲁棒性，适宜于噪声干扰情况下现场移动荷载识别。

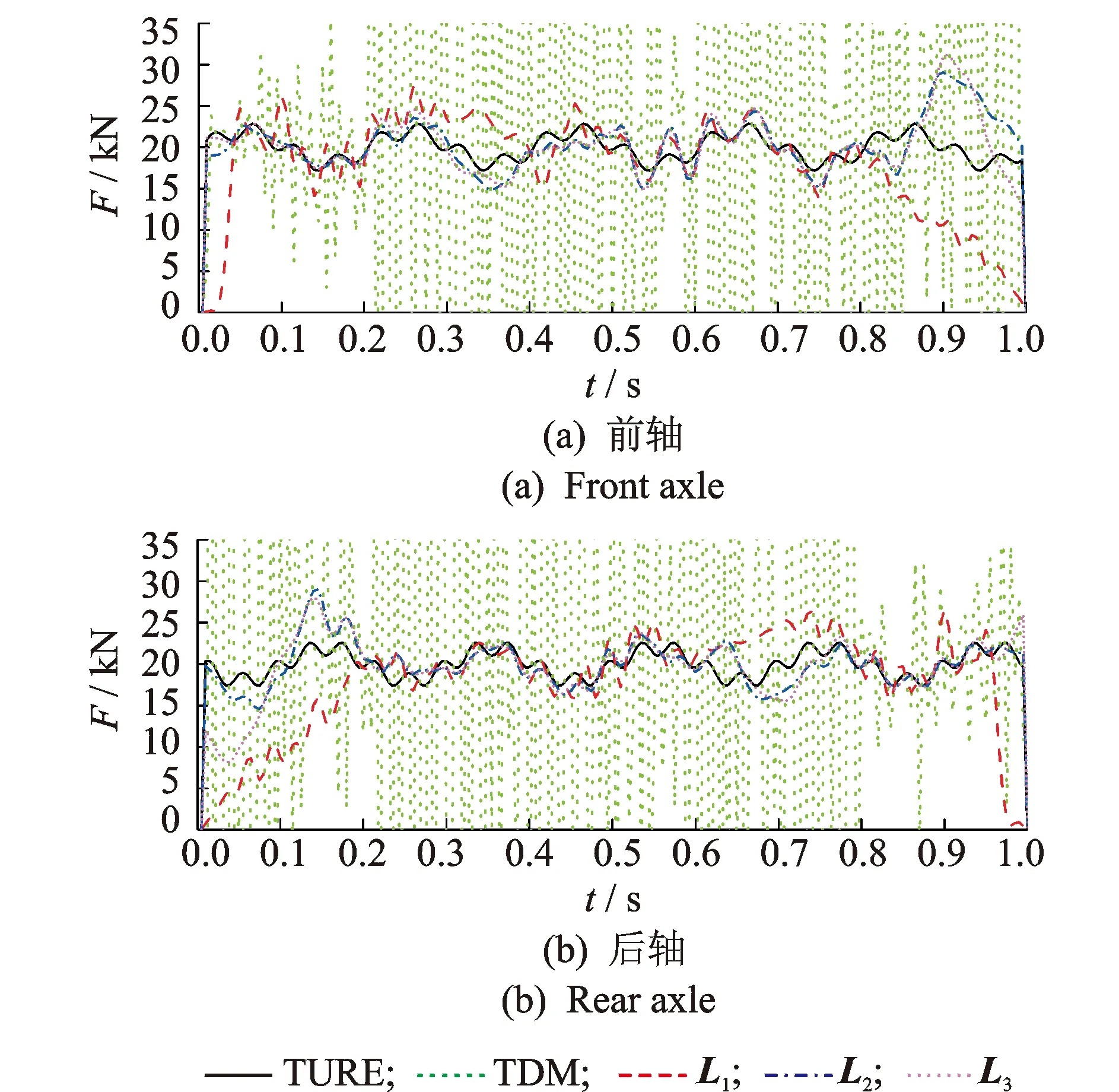
图3 5%噪声时采用不同正则化矩阵弯矩响应识别结果比较(1/4，1/2和3/4跨长的3个弯矩响应)Fig.3 Comparison on identified results from bending moment responses by TGSVD with three different regularization matrixes when the noise is 5%

表2 TDM 与TGSVD识别误差比较

响应类型对TDM识别精度影响明显，当响应类型全部为弯矩响应时，识别精度明显偏低，当响应类型全部为加速度响应时，识别精度可以接受。图4为由加速度响应识别移动荷载时，TDM与TGSVD识别结果比较。在10%噪声水平下，除前轴下桥和部分时段识别误差较大，大多数时段TDM识别结果均可接受，较仅由弯矩响应识别精度有很大提高。采用L2和L3正则化矩阵TGSVD识别精度均很高，较仅由弯矩响应识别精度略有提高，识别结果受响应类型不同影响较小。

测点数量尤其是加速度测点数量对TDM识别精度影响很大，TDM识别方法的效果受测点数量和类型变化影响明显。当响应数量较少且含有弯矩响应时(1/4跨长的1个弯矩响应和1/4跨长的1个加速度响应工况)，在10%噪声水平下，TDM前轴识别误差为6 824%，后轴识别误差为5 514%，而TGSVD采用L2正则化矩阵前轴识别误差仅为7.7%，后轴识别误差仅为8.0%。图5为10%噪声水平下该工况两种方法识别结果比较。由图5可知TDM无法识别移动荷载，TGSVD采用L3正则化矩阵识别时波动较大，采用L2正则化矩阵识别精度很高，这也说明无论是由弯矩响应、加速度响应及两者组合响应识别移动荷载时，L2均是最优正则化矩阵。数值仿真结果表明，L1正则化矩阵效果较差，L2和L3正则化矩阵效果较好，其中L2正则化矩阵效果最好。

图4 10%噪声时TDM和TGSVD由加速度响应识别结果比较(1/4和1/2跨长的2个加速度响应)Fig.4 Comparison on identified results from acceleration responses by TDM and TGSVD when the noise is 10%

图5 10%噪声时TDM和TGSVD由弯矩和加速度组合响应识别结果比较(1/4跨长的1个弯矩响应和1/4跨长的1个加速度响应)Fig.5 Comparison on identified results from bending moment and acceleration responses by TDM and TGSVD when the noise is 10%

3 结 论

1) TGSVD识别误差受噪声干扰影响很小，具有良好的鲁棒性，适宜于噪声干扰情况下现场移动荷载识别。

2) TGSVD各种工况下识别精度均很高，识别结果受响应类型、响应数量及其组合情况影响很小，有利于测点较少、响应类型单一环境下现场移动荷载识别。

3) 通过3种正则化矩阵识别精度比较，L2和L3正则化矩阵效果较好，其中L2正则化矩阵抗噪性强、识别精度高且适用于各种响应组合工况，为最优正则化矩阵，在现场移动荷载识别时，建议TGSVD优先选用L2正则化矩阵。

[1] 李忠献, 陈锋. 简支梁桥与多跨连续梁桥上移动荷载的识别与参数分析[J]. 工程力学, 2006, 23(12): 91-99.

Li Zhongxian, Chen Feng. Identification and parametric analysis of moving loads on simply supported and multi-span continuous bridges[J]. Engineering Mechanics, 2006, 23(12): 91-99. (in Chinese)

[2] 袁向荣. 移动荷载识别的响应曲线滑动拟合法[J]. 振动、测试与诊断, 2007, 27(4): 320-323.

Yuan Xiangrong. Moving fitting method in moving force identification[J]. Journal of Vibration, Measurement & Diagnosis, 2007, 27(4): 320-323. (in Chinese)

[3] Law S S, Chan T H T. Regularization in moving force identification[J]. Journal of Engineering Mechanics, 2001, 127(2): 136-148.

[4] Law S S, Chan T H T, Zeng Q H. Moving force identification: a time domain method[J]. Journal of Sound and Vibration, 1997, 201(1): 1-22.

[5] Law S S, Chan T H T, Zeng Q H. Moving force identification: a frequency-time domain method[J]. Journal of Dynamic System, Measure Control, 1999,121: 394-401.

[6] 卜建清, 罗韶湘, 朱信群. 基于广义正交函数和正则化的移动荷载识别法[J]. 振动、测试与诊断, 2005, 25(1): 36-39.

Bu Jianqing, Luo Shaoxiang, Zhu Xinqun. Moving loads identification based on generalized orthogonal function and regularization technique[J]. Journal of Vibration, Measurement & Diagnosis, 2005, 25(1): 36-39.(in Chinese)

[7] 尤琼, 史治宇. 基于区间B样条小波有限元的移动荷载识别[J]. 工程力学, 2011, 28(5): 35-40.

You Qiong, Shi Zhiyu. Moving force identification based on B-spline wavelet on the interval[J]. Engineering Mechanics, 2011, 28(5): 35-40. (in Chinese)

[8] 余岭, 陈震. 桥梁移动荷载识别的不适定性及其试验研究[J]. 振动与冲击, 2007, 26(12): 6-9.

Yu Ling, Chen Zhen. Experimental study on ill-conditioning problem in identification of moving vehicle loads on bridges[J]. Journal of Vibration and Shock, 2007, 26(12): 6-9. (in Chinese)

[9] 陈锋,李忠献. 梁桥上移动荷载识别中的测点优化[J]. 振动、测试与诊断, 2009, 29(2): 218-222.

Chen Feng, Li Zhongxian. Sensor placement optimization for moving load identification on girder bridges[J]. Journal of Vibration, Measurement & Diagnosis, 2009, 29(2): 218-222. (in Chinese)

[10]张青霞, 段忠东, Lukasz J, 等. 基于形函数方法快速识别结构动态荷载的试验验证[J]. 振动与冲击, 2011, 30(9): 98-102.

Zhang Qingxia, Duan Zhongdong, Lukasz J, et al. Experimental validation of a fast dynamic load identification method based on load shape function[J]. Journal of Vibration and Shock, 2011, 30(9): 98-102.(in Chinese)

[11] 王蕾, 侯吉林, 欧进萍. 基于荷载形函数的大跨桥梁结构移动荷载识别[J]. 计算力学学报, 2012, 29(2): 153-158.

Wang Lei, Hou Jilin, Ou Jinping. Moving force identification based on load shape function for a long-span bridge structure[J]. Chinese Journal of Computational Mechanics, 2012, 29(2): 153-158. (in Chinese)

[12] 夏樟华, 宗周红, 李嘉维, 等. 基于健康监测系统的大跨度连续刚构桥移动荷载识别[J]. 中国公路学报, 2012, 25(5): 95-103.

Xia Zhanghua, Zong Zhouhong, Li Jiawei, et al. Moving load identification of long span continuous rigid frame bridges based on health monitoring system[J]. China Journal of Highway and Transport, 2012, 25(5): 95-103. (in Chinese)

[13] 余岭, Chan T H T. 桥梁时变移动车载的间接识别[J]. 振动工程学报, 2005, 18(1): 99-102.

Yu Ling, Chan T H T. Indirect identification of time-varying moving vehicle loads on bridges[J]. Journal of Vibration Engineering, 2005, 18(1): 99-102. (in Chinese)

[14] Hansen P C. Regularization, GSVD and truncated GSVD[J]. BIT,1989,29: 491-504.

[15] 陈震, 余岭. 基于截断GSVD方法的桥梁移动荷载识别, 振动与冲击[J]. 振动与冲击, 2014, 33(10): 97-100.

Chen Zhen, Yu Ling. Identification of dynamic axle Loads on bridge based on truncated generalized singular value decomposition[J]. Journal of Vibration and Shock, 2014, 33(10): 97-100. (in Chinese)

*国家自然科学基金资助项目(51278226)；河南省教育厅科学技术研究重点资助项目(14B560018)；华北水利水电大学青年科技创新人才资助项目(70473)

2013-06-25；

2013-08-08

10.16450/j.cnki.issn.1004-6801.2015.01.004

O327； TU311; TH113

陈震，男，1981年2月生，博士、副教授。主要研究方向为移动荷载动态识别、结构破坏数值仿真。曾发表《桥梁移动荷载识别的不适定性及其试验研究》(《振动与冲击》2007年第12期)等论文。 E-mail: yuchenfish@163.com 通信作者简介：余岭，男，1963年5月生，博士、教授、博士生导师。主要研究方向为结构健康监测、结构损伤与荷载协同识别。 E-mail：lyu1997@163．com